6. Ошибки параллельных опытов. Дисперсия параметра оптимизации. Проверка однородности дисперсий.

Ошибки параллельных опытов

Каждый эксперимент содержит элемент неопределен­ности вследствие ограниченности экспериментального ма­териала. Постановка повторных (или параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях несколько раз и затем бе­рется среднее арифметическое всех результатов. Среднее арифметическое   равно сумме всех п отдельных резуль­татов, деленной на количество параллельных опытов п

.

Отклонение результата любого опыта от среднего арифметического можно представить как разность   где   – результат отдельного опыта. Наличие откло­нения свидетельствует об изменчивости, вариации значе­ний повторных опытов. Для измерения этой изменчи­вости чаще всего используют дисперсию. Диспер­сией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозна­чается s² и выражается формулой

.

где (n – 1) – число степеней свободы, равное количе­ству опытов минус единица. Одна степень свободы исполь­зована для вычисления среднего.

Корень квадратный из дисперсии, взятый с положи­тельным знаком, называется средним квадратическим от­клонением, стандартом или квадратичной ошибкой

Все ошибки принято разделять на два класса: система­тические и случайные.

Систематические ошибки порождаются причинами, действующими регулярно, в определенном направлении.

Случайными ошибками называются те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и которые невозможно учесть заранее.

Очень важно исключить из экспе­риментальных данных грубые ошибки, так называемый брак при повторных опытах. Для отброса оши­бочных опытов существуют правила. Для определения брака используют, например, кри­терий Стьюдента

.

Значение t берут из таблицы t-распределения Стьюдента. Опыт считается бракованным, если эксперименталь­ное значение критерия t по модулю больше табличного значения.

Дисперсия параметра оптимизации

Дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов, т.е. подсчете дисперсии параметра оптимизации   или, дисперсии воспроизводимости эксперимента 

При подсчете дисперсии параметра оптимизации квад­рат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просумми­ровать по числу опытов в матрице N, а затем разделить на N(n - 1):

,

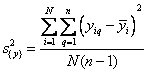Где i = 1, 2, …, N;      q = 1, 2, …, n.

 Проверка однородности дисперсий может осуществляться двумя способами: при равных выборках (1) и при различных выборках (2).

1. Нулевая гипотеза состоит в том, что все k совокупностей выборок имеют равные дисперсии: σ₁² = σ₂² = σ₃² =… = σ₃² = σ_к² = σ²

Пусть среди выборочных дисперсий есть такая, что она максимальна и равна S_max².

Альтернативная гипотеза H₁: σ_max² > σ²

Критерий Кохрена:

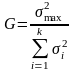
В зависимости от уровня значимости α, числа степеней свободы m=n-1, и числа сравниваемых дисперсий k находим по таблицам G_{α, m, k}

Критическая область соответствует G ≥ G_{α, m, k}

О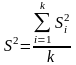 ценка обобщенной дисперсии будет

2. Если число измерений в различных сериях неодинаково используется критерий Бартлета

Обозначим выборочную дисперсию j-й выборки S_j²

Т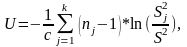 огда величина критерия будет

З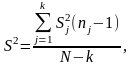 десь:

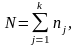
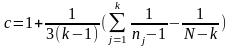
Справедливость гипотезы проверяется критерием Пирсона χ² с (k-1) степенями свободы.

Если U < χ² , при (k-1) и (1-q) – дисперсии однородны.

Если U > χ² , при (k-1) и (1-q) – дисперсии не однородны.