1. Электростатическое поле является потенциальным и его энергия тоже будет потенциальной

Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется, заряды только перераспределяются(для замкнутой системы)

Электрический заряд – это внутреннее свойство тел или частиц, характеризующее их способность к электромагнитным взаимодействиям. [Q]=1 Kл

, e=1.6 * 10^-19 Кл, n-целое число

2. Точечный заряд (q) – заряженное тело, размеры которого пренебрежительно малы по сравнению с расстоянием до других заряженных тел, с которым оно взаимодействует.

Закон Кулона: сила взаимодействия двух точечных зарядов в вакууме прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними

   — коэффициент пропорциональности

  k=9·10⁹ Н·м²/Кл² 

 ≈ 8,85·10⁻¹² Ф/м — электрическая постоянная.

В Векторной форме Закон Кулона выглядит так:

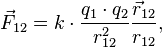
Закон Кулона действует при размерах 10⁷- 10^-15м на точечные заряды

3. Вокруг заряда всегда есть электрическое поле

С иловой характеристикой поля создаваемого зарядом q является отношение силы действующей на заряд к величине этого заряда называемое напряженностью электростатического поля

Н апряженность в векторной форме

здесь r – расстояние от заряда до точки, где мы изучаем это поле.

напряженность - вектор, который равен силе, действующей в данной точке на помещенный в нее пробный единичный положительный заряд.

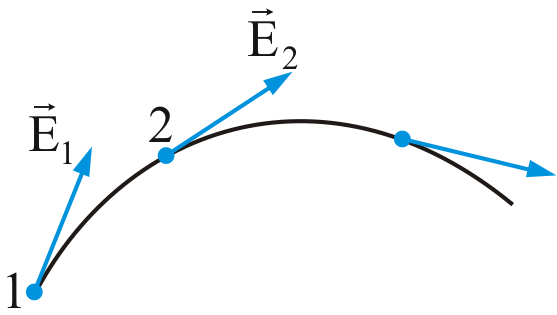электростатическое поле изображают с помощью силовых линий

силовые линии – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности

О днородное поле (все линии параллельны)

Н еоднородное поле

густота силовых линий определяет поток вектора напряженности (Ф)

4. Поток вектора напряженности Ф через поверхность S определяется Полным числом силовых линий, проходящих через поверхность S

В векторной форме можно записать

– скалярное произведение двух векторов, где вектор .

Таким образом, поток вектора есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.

Д ля первого рисунка – поверхность А₁ окружает положительный заряд и поток здесь направлен наружу, т.е.

Поверхность А₂ – окружает отрицательный заряд, здесь и направлен внутрь.

Общий поток через поверхность А равен нулю

5. Р езультирующая сила определится выражением:

– это принцип суперпозиции или независимости действия сил

н апряженность поля подчиняется тому же принципу суперпозиции что и сила

Если поле создается не точечными зарядами, то тогда используется метод интегрирования, дифференцирования

П лотности заряда:

• – линейная плотность заряда, измеряется в Кл/м;

• поверхностная плотность заряда измеряется в Кл/м²;

• – объемная плотность заряда, измеряется в Кл/м³.

6. Электрическое поле диполя

Для фиксированных угловых координат (то есть на луче, идущем из центра электрического диполя на бесконечность) напряжённость статического электрического поля диполя или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент, на больших расстояниях r асимптотически приближается к виду r⁻³, электрический потенциал — к r⁻². Таким образом, статическое поле диполя убывает на больших расстояниях быстрее, чем поле простого заряда (но медленнее, чем поле любого более старшего мультиполя).

Напряжённость электрического поля и электрический потенциал неподвижного или медленно движущегося диполя (или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент) с электрическим дипольным моментом   на больших расстояниях в главном приближении выражается как:

в СИ: 

где   — единичный вектор из центра диполя в направлении точки измерения, а точкой обозначено скалярное произведение.

7. Поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность s.

п 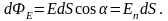оток вектора напряженности через произвольную элементарную площадку dS будет равен:

Т .е. в однородном поле

В произвольном электрическом поле

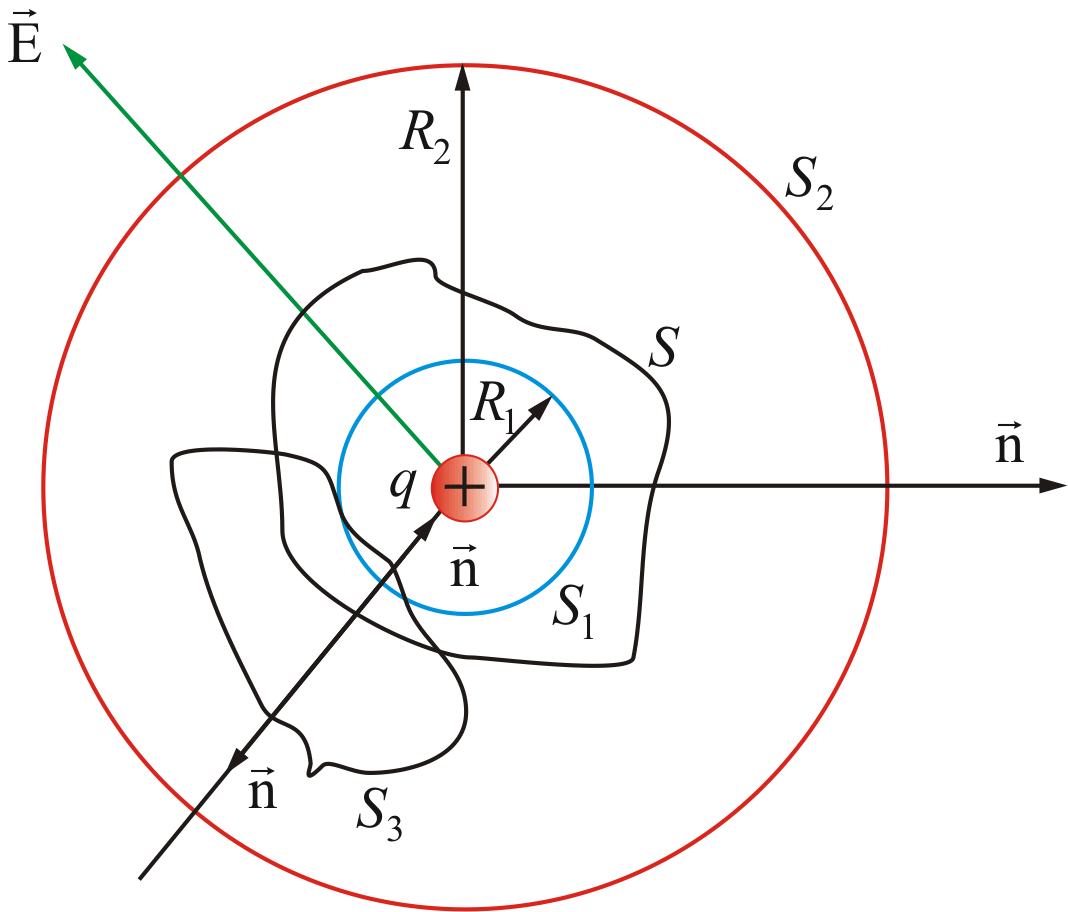
В каждой точке поверхности S₁ проекция Е на направление внешней нормали одинакова и равна

Тогда поток через S₁

через сферу S₂

И з непрерывности линии следует, что поток и через любую произвольную поверхность S будет равен этой же величине:

– теорема Гаусса для одного заряда.

– теорема Гаусса для нескольких зарядов

П олный поток проходящий через S₃, не охватывающую заряд q, равен нулю:

Электрические заряды могут быть «размазаны» с некоторой объемной плотностью различной в разных местах пространства:

З десь dV – физически бесконечно малый объем

Суммарный заряд объема dV будет равен:

– теорема Остроградского-Гаусса, если заряд неравномерно

распределен по объему

8. В еличину, являющуюся пределом отношения к V, при , называют дивергенцией поля е

дивергенция является скалярной функцией координат.

В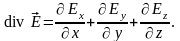 декартовой системе координат

Это теорема Остроградского-Гаусса в дифференциальной форме.

векторный дифференциальный оператор (Набла)

где i, j, k – орты осей (единичные векторы).

- дифференциальная форма теоремы Остроградского-Гаусса.

В тех точках поля, где – источники поля (положительные заряды),

где – стоки (отрицательные заряды).

Л инии напряженности выходят из источников и заканчиваются в стоках.

9. Описание электростатического поля мы рассматривали с помощью вектора напряженности : Существует и другой способ описания поля – с помощью потенциала. Однако для этого необходимо сначала доказать, что силы электростатического поля консервативны, а само поле потенциально.

В любой точке этого поля на пробный точечный заряд q' действует сила F:

где F(r) – модуль вектора силы , – единичный вектор, определяющий положение заряда q относительно q', ε₀ – электрическая постоянная

л 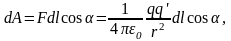юбое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от формы пути, а только от положения конечной и начальной точек.

Работа на пути dl равна:

г де dr – приращение радиус-вектора при перемещении на dl;

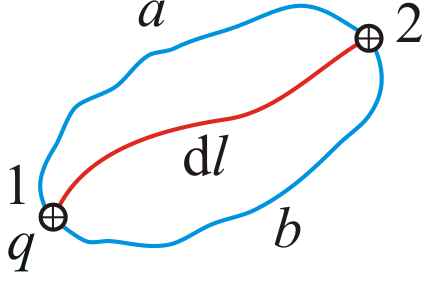
Полная работа при перемещении из точки 1 в точку 2 равна интегралу:

Работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. Следовательно, силы поля консервативны, а само поле – потенциально.

Е сли единичный заряд q – положительный, то элементарная работа сил поля будет равна:

Т огда вся работа равна:

Т акой интеграл по замкнутому контуру называется циркуляцией вектора

по произвольному замкнутому пути: - теорема о циркуляции .

10. э лектростатическое поле потенциально. Следовательно, можно ввести функцию состояния, зависящую от координат – потенциальную энергию.

Общая работа А будет равна сумме работ каждой силы:

Р аботу сил электростатического поля можно выразить через убыль потенциальной энергии – разность двух функций состояний:

Это выражение для работы можно переписать в виде:

С опоставляя эти две формулы получаем выражение для потенциальной энергии заряда q' в поле заряда q:

11. в ведем скалярную величину, являющуюся энергетической характеристикой собственно поля – потенциал:

п отенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд