Узлы сопряжения оболочек

В реальных конструкциях края оболочек прикрепляются к другим оболочкам (днища, крышки, люки, патрубки и т. д.). В таких узлах сопряжения возникают дополнительные, так называемые краевые, нагрузки, вызывающие местные напряжения изгиба в материале сопрягаемых элементов. Краевая сила Q₀ и краевой момент Мо являются реакциями заделки края оболочки, которому мешает деформироваться сопрягаемая деталь. Причинами появления краевых нагрузок и Q₀ и Мо могут быть

1) заделка края оболочки (рис. 3);

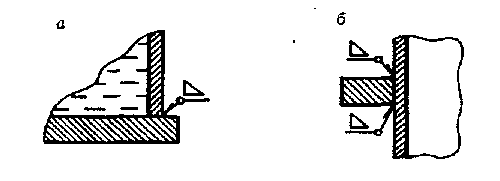
Рис. 3. Примеры соединения края оболочки:

а – с толстым плоским днищем; 6 – с кольцом жесткости

2) изменение геометрических размеров (формы) оболочки при переходе от одного сечения к другому (рис. 4);

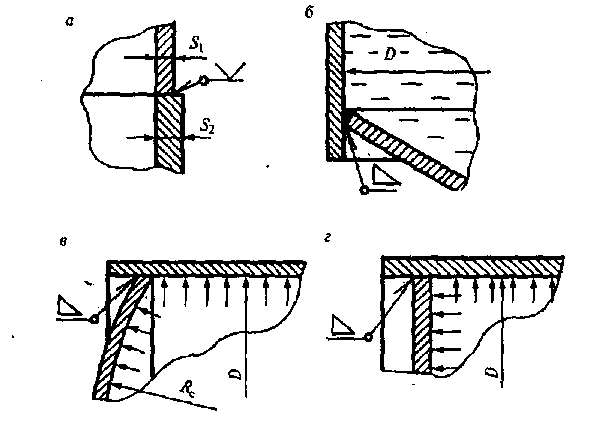
Рис. 4. Примеры изменения геометрических размеров оболочки:

а – соединение цилиндрических обечаек разной толщины; б, в, г – соединения

обечаек разной форм

3) изменение нагрузки при переходе от одного сечения к другому (рис. 5);

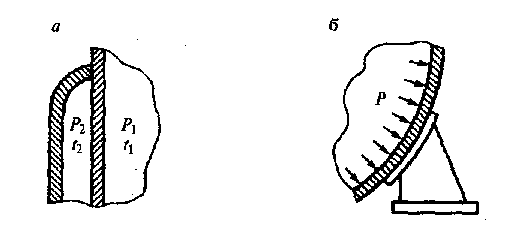
Рис. 5. Примеры изменения нагрузок, действующих на оболочки:

а – соединение корпуса аппарата с его рубашкой; б – соединения оболочки с опорой

4) изменение свойств материала (модуля упругости Е, коэффициента линейного расширения , коэффициента Пуассона  и др.) при переходе от одного сечения к другому (рис. 6).

Рис. 6. Соединение оболочек, изготовленных из коррозионно-стойкой (1)

и углеродистой (2) стали

Для определения Q₀ и М₀ составляются так называемые уравнения совместности радиальных _р и угловых _P деформаций. Сущность этих уравнений заключается в том, что для нормальной работы аппарата в узле сопряжения не должно быть никаких относительных перемещений сопрягаемых деталей, т. е. необходимо выполнение условий, когда _р и угловых _P деформаций края одной детали от действующих внешних и краевых нагрузок равны соответствующим суммам радиальных и угловых деформаций края другой детали от действующих на нее активных и реактивных нагрузок. Приняв для края оболочки положительными радиальные перемещения  в направлении от ее оси, а угловые перемещения  в направлении по часовой стрелке, получим для правой части оболочек уравнения совместности радиальных и угловых деформаций:

,

где , , , , , – соответственно радиальные и угловые деформации края цилиндрической обечайки под действием нагрузок P, Q₀ и M₀; , , , , , – соответственно радиальные и угловые деформации края цилиндрической обечайки под действием нагрузок P, Q, Q₀ и M₀

Пример. Составим эти уравнения для узла сопряжения сферической и цилиндрической оболочек, находящихся под внутренним давлением (рис. 7).

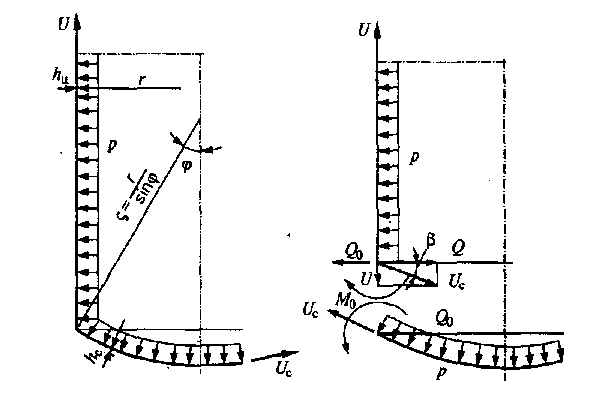
Рис. 7. Схема к определению краевых сил и моментов в узле соединения сферической

и цилиндрической оболочек: U и U_с – меридиональные усилия соответственно

цилиндрической и сферической оболочек

Мысленно рассечем узел плоскостью, перпендикулярной к оси симметрии. Образуется статически определимая система, состоящая из двух оболочек.

К оболочкам приложена заданная внешняя нагрузка (внутреннее давление Р), распорная сила Q, действующая на край сферической оболочки, а также неизвестные краевые нагрузки Q₀ и М₀.

Приняв для края оболочки положительными радиальные перемещения  в направлении от ее оси, а угловые перемещения  в направлении по часовой стрелке, получим с учетом этого правила знаков для правой части оболочек (рис. 7) уравнения совместности радиальных и угловых деформаций.

Если нагруженная цилиндрическая оболочка жестко защемлена в недеформируемой детали (во фланце большой толщины) система уравнений упрощается и принимает вид

Если оболочка шарнирно соединяется с недеформируемой деталью (прокладка), то М₀=0, необходимость в составлении второго уравнения системы отпадает и для нахождения Q₀ достаточно одного уравнения

.

Деформации, а следовательно, и напряжения изгиба от действия краевых нагрузок носят локальный характер.

Сечения обечаек, отстоящие от края на расстоянии , можно считать бесконечно удаленными от него, и действием Q₀ и М₀ на эти сечения можно пренебречь.  – коэффициент затухания деформации вдоль образующей оболочки (определяется по табличным формулам); – для цилиндрической обечайки.

Выражения для вычисления перемещений (, ), усилий (U, Т, Р), моментов (М_m, M_t М_r) и напряжений на краю цилиндрических, сферических, конических и эллиптических оболочек можно найти по табличным данным.

Для нашего случая напряжения на наружной и внутренней поверхностях края оболочки:

меридиональное

;

кольцевое

;

максимальное

,

где , – соответственно сумма меридиональных и сумма тангенциальных (окружных) усилий, возникающих на краю обечайки от действия давления P, краевой Q₀ и распорной Q сил, краевого момента M₀; , –соответственно сумма меридиональных и сумма тангенциальных (кольцевых) моментов, возникающих на краю обечайки от действия нагрузок P, (Q₀–Q) и M₀.