Постановка многокритериальной задачи линейного программирования

Постановка задачи:

Дано: область D допустимых значений переменных, определяемая совокупностью линейных равенств и неравенств; критерии Ci, оценивающие качество решения.

Каждый из критериев линейно связан с переменными:

где n — число переменных (j=l,...,n); - числовые коэффициенты.

Требуется: найти решение X в области D, при котором достигаются наиболее приемлемые значения по всем критериям. Иначе говоря, нужно найти такие критериальные оценки, при которых достигается максимальное значение априори неизвестной функции полезности ЛПР. Эта задача решается с помощью человеко-машинных процедур.

Человекомашинные процедуры

Средством исследования области допустимых решений, приводящим к желаемому выбору наилучшего решения, являются человекомашинные процедуры (ЧМП), представляющие собой процедуры общения ЛПР и компьютера. Они состоят из

совокупности шагов, каждый из которых включает в себя фазу анализа, выполняемого ЛПР, и фазу расчетов, выполняемых компьютером.

Фаза расчетов (компьютер):

• используя полученную от ЛПР на предыдущем шаге информацию, проводит дополнительные расчеты;

• вычисляет решение, соответствующее последней информации ЛПР;

• вырабатывает вспомогательную информацию для ЛПР.

Фаза анализа (ЛПР):

• оценивая предъявленное решение (или совокупность решений), определяет, является ли решение (одно из решений) приемлемым; если да, то ЧМП окончена; в противном случае ЛПР анализирует вспомогательную информацию;

• сообщает дополнительную информацию, с помощью которой компьютер вычисляет новое решение.

Существует большое количество ЧМП. Различные ЧМП отличаются друг от друга содержанием и способом выполнения каждой из фаз. Первые из разработанных ЧМП основаны на использовании информации об относительной важности критериев.

Весовые коэффициенты важности критериев

При появлении многокритериальных задач возникли дополнительные трудности их решения, связанные с получением информации от ЛПР, Естественной реакцией на это было стремление получить такую информацию сразу и быстро устранить многокритериальность. Этот подход был реализован путем объединения многих критериев в один с помощью так называемых весовых коэффициентов важности критериев. Глобальный критерий вычисляется по формуле

Идея такого объединения состоит в том, что ЛПР назначает числа (часто по численной шкале 1-100), представляющие для него ценность рассматриваемого критерия. Считается, что ЛПР может назначить такие числа. Далее, весовые коэффициенты

нормируются на основе условия (2).

Следовательно, формально задача сводится к нахождению весов. Возникла идея, что эти веса можно получить от ЛПР оперативно. Если ЛПР затрудняется в начале процесса решения (до изучения области D) сразу назвать эти веса, то можно построить

ЧМП следующего содержания: ЛПР назначает первоначальные веса, смотрит на решение и корректирует веса до получения удовлетворительного результата.

Классификация чмп

В предложена классификация ЧМП, основанная на характере информации, получаемой от ЛПР на фазе анализа.

Первая группа ЧМП - прямые ЧМП, в которых ЛПР непосредственно назначает веса критериев и корректирует их на основе полученных решений.

Для второй группы ЧМП задача ЛПР состоит в сравнении многокритериальных решений. Эта группа называется ЧМП оценки векторов.

Третья группа требует от ЛПР наложения ограничений на значения критериев и, следовательно, на область допустимых значений. ЧМП этой группы называются ЧМП поиска удовлетворительных решений.

Перед тем как перейти к рассмотрению ЧМП каждой группы, следует указать на общие предварительные этапы, встречающиеся во многих ЧМП.

Перед решением задачи рекомендуется произвести нормированиекритериев, определив диапазон их изменения от 0 до 1:

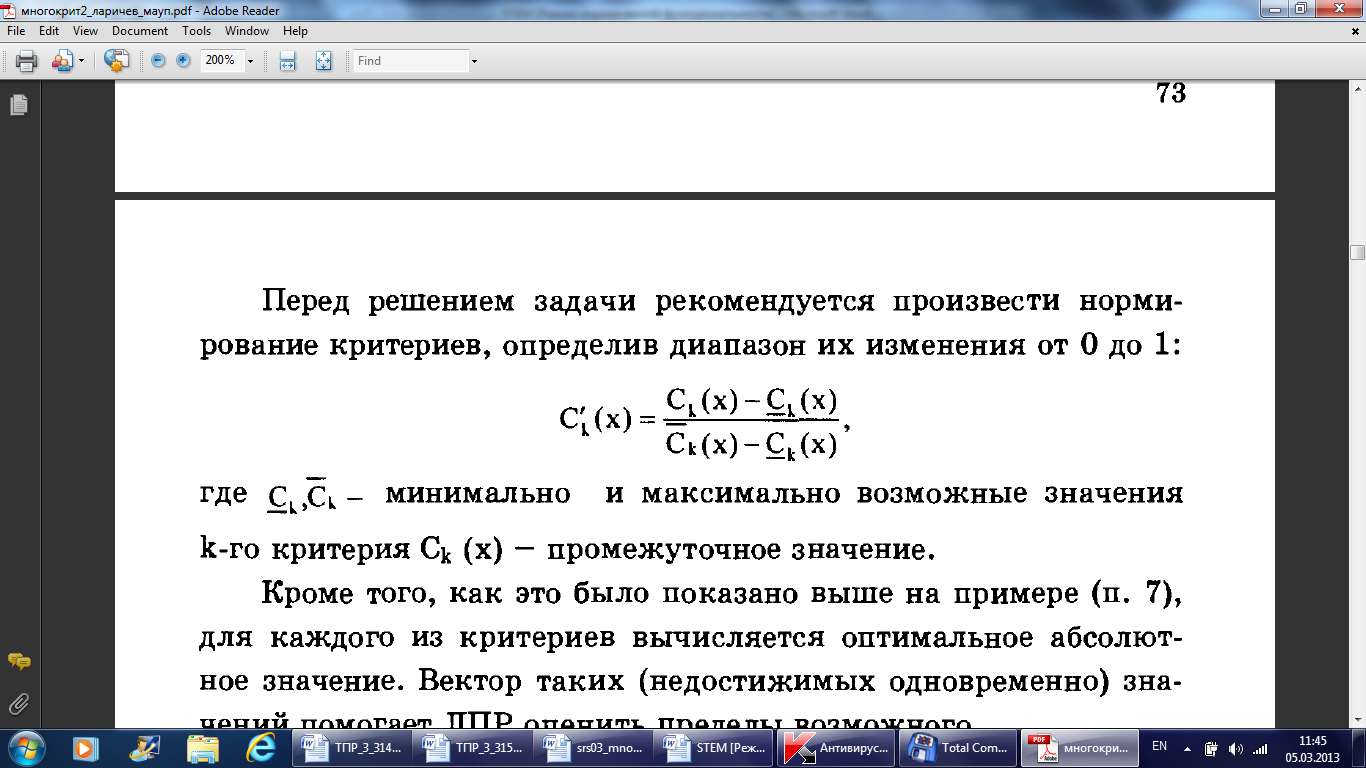Кроме того, как это было показано выше на примере (п. 7), для каждого из критериев вычисляется оптимальное абсолютное значение. Вектор таких (недостижимых одновременно) значений помогает ЛПР оценить пределы возможного.