Введение

Данное учебно-методическое пособие содержит образцы решения задач на составление уравнений прямых по условиям, которые их определяют.

Так же в нем представлены:

- структурная схема основных уравнений прямой, формул вычисления угловых коэффициентов, условий параллельности и перпендикулярности прямых (приложение А);

- алгоритмы составления уравнений:

а) медианы треугольника (приложение Б);

б) средней линии треугольника (приложение В) ;

в) высоты треугольника (приложение Г) ;

г) биссектрисы треугольника (приложение Д)

Представлены образцы решения задач:

Задача 1

Даны вершины треугольника: , , . Составить уравнение

медианы из вершины С и найти её длину.

Задача 2

Даны стороны треугольника: , ,

. Составить уравнение высоты, проведенной из вершины В

и найти её длину.

Задача 3

Даны вершины треугольника: , , . Составить уравнение

биссектрисы, проведенной из угла А.

Задача 4

Даны три последовательные вершины параллелограмма: , , .

Составить уравнения сторон параллелограмма.

Задача 5

В ромбе уравнения двух сторон заданы уравнениями: и

. Диагонали пересекаются в точке N (5;5). Составить уравнения

двух других сторон ромб . Найти площадь ромба.

Задача 6

В прямоугольнике АВСD сторона CD задана уравнением , вершина

В (3;7), диагонали пересекаются в точке L(5;2). Найти площадь прямоугольника.

Задача 7

Равнобедренная трапеция с основаниями 10 и 4 единиц имеет острый угол 30⁰.

Написать уравнения сторон трапеции, приняв за ось ОХ меньшее основание трапеции,

а за ось ОУ ось симметрии трапеции.

Задача 8

Найти проекцию точки на прямую, проходящую через точку и отсекающую на осях координат равные отрезки.

Данное учебно - методическое пособие рекомендуется использовать при выполнении самостоятельной работы студента по модулю ЕН.01.М.02 Аналитическая геометрия на плоскости, учебный элемент 02.02 Линии первого порядка, а так же практической работы 4 Составление уравнений прямых на плоскости

Образцы решения типовых задач

Задача 1

Даны вершины треугольника: , , . Составить уравнение

медианы из вершины С и найти её длину.

Дано:

, , .

Составить уравнение медианы из вершины С и найти её длину.

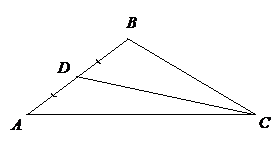
Рис.1

Решение

1 Найдем координаты середины стороны АВ (рис.1):

,

,

.

2 Составим уравнение медианы

Воспользуемся уравнением прямой проходящей через две точки:

, , .

Упростим, полученное уравнение и запишем в общем виде:

,

,

3 Найдем длину медианы

Для вычисления воспользуемся формулой вычисления расстояния между двумя точками:

Ответ: , .

Задача 2

Даны стороны треугольника: , ,

. Составить уравнение высоты, проведенной из вершины В

и найти её длину

Дано:

,

,

Составить уравнение высоты, проведенной из вершины В и найти её длину.

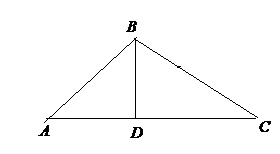
Рис.2

Решение

1 Найдем точку В

Точку В треугольника АВС (рис. 2) найдем как точку пересечения прямых АВ и ВС.

Решим совместно уравнения прямых:

получим ,

2 Составим уравнение высоты (рис. 2)

Так как (условие перпендикулярности прямых).

Угловой коэффициент прямой ( ) найдем из общего уравнения

по формуле , , .

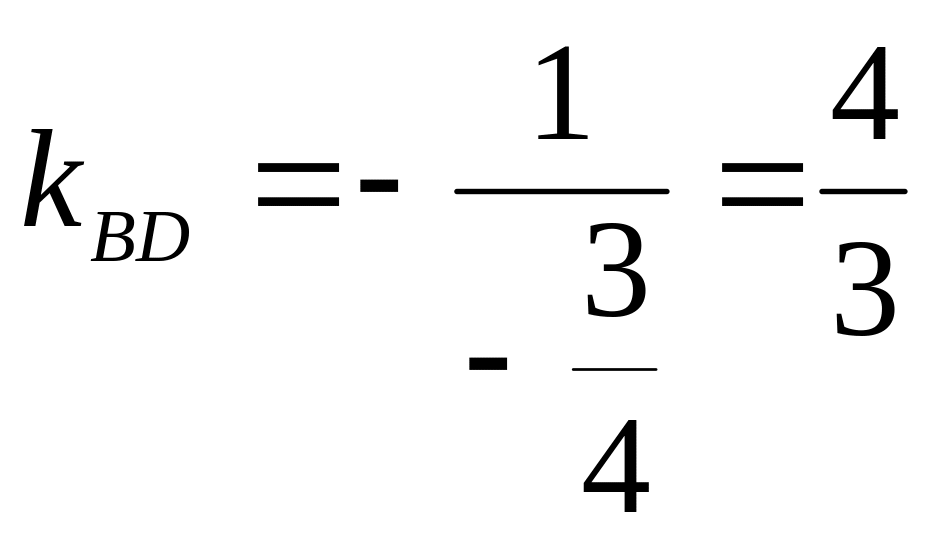Воспользуемся уравнением «пучка» прямых: , .

Упростим, полученное уравнение:

,

3 Найдем длину высоты как расстояние от точки В до прямой ,

по формуле вычисления расстояние от точки до прямой:

.

Ответ: ,

Задача 3

Даны вершины треугольника: , , . Составить уравнение

биссектрисы, проведенной из угла А

Дано:

, , .

Составить уравнение биссектрисы, проведенной из угла А.

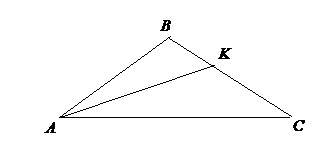
Рис.3

Решение

1 Пусть К – точка пересечения биссектрисы со стороной ВС (рис.3). По свойству

биссектрисы внутреннего угла треугольника следует, что .

Найдем длины сторон и :

Следовательно, .

2 Найдем координаты точки К

Так как известно отношение, в котором точка К делит отрезок СВ, то координаты точки

К определяются по формулам:

,

,

.

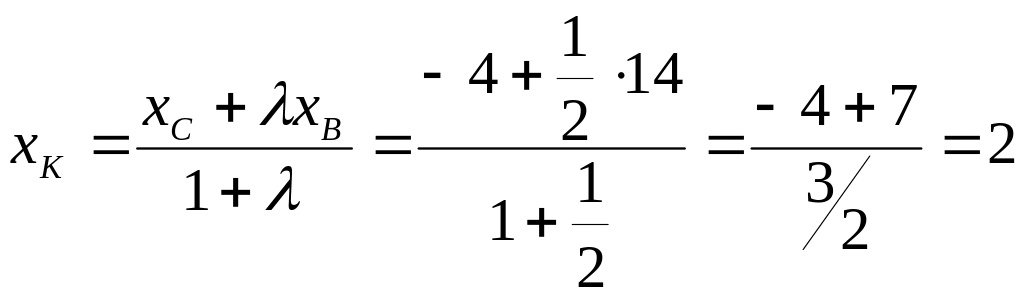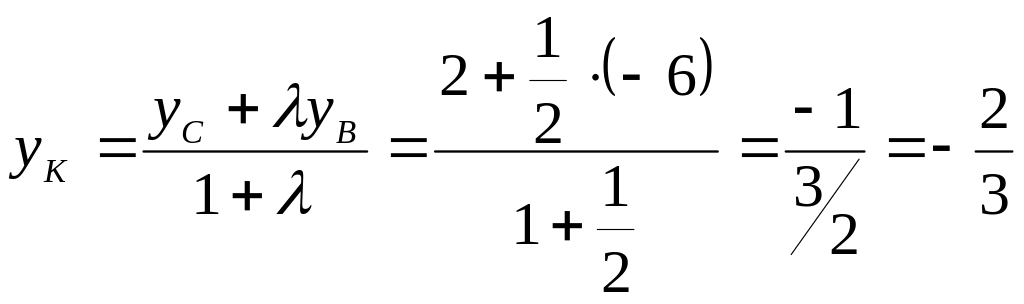3 Составим уравнение биссектрисы АК

Воспользуемся уравнением прямой проходящей через две точки:

, ,

,

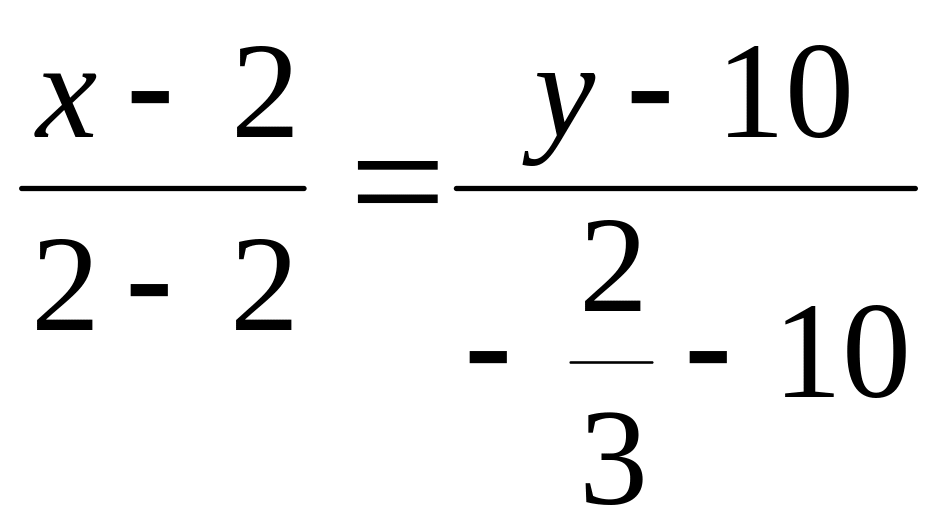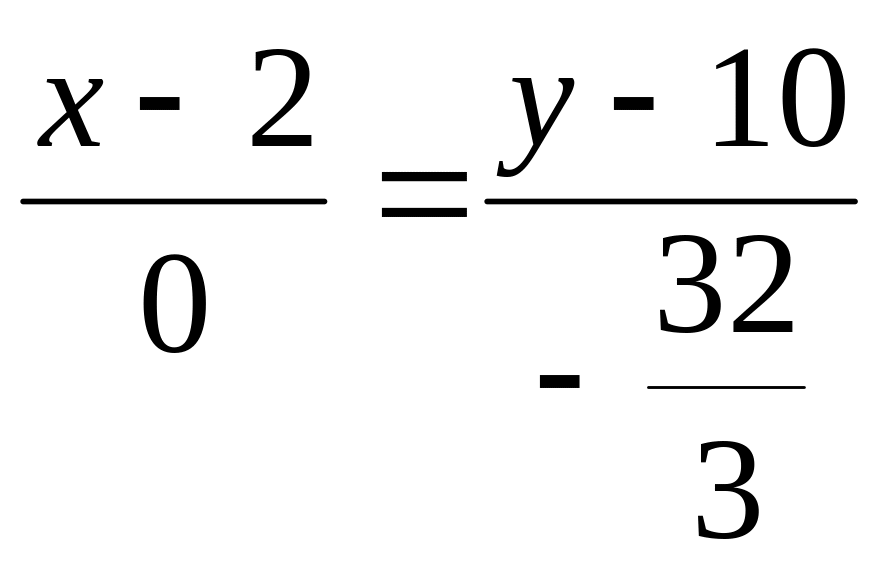
(прямая АК параллельна оси ординат)

Ответ:

Задача 4

Даны три последовательные вершины параллелограмма: , , .

Составить уравнения сторон параллелограмма

Дано:

АВСD – параллелограмм

, , .

Составить уравнения сторон параллелограмма.

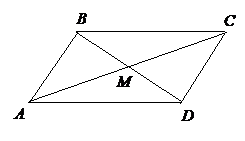
Рис.4

Решение

1 Составим уравнения сторон и (рис.4)

Воспользуемся уравнением прямой, проходящей через две точки:

: , ,

,

.

Аналогично составим уравнение ВС:

2 Найдем координаты точки :

Диагонали параллелограмма в точке пересечения делятся пополам, тогда

,

,

.

3 Найдем координаты точки :

, откуда ,

, откуда ,

.

4 Составим уравнения сторон и :

: , тогда

, , .

: , тогда

, , .

Ответ: : ; :

: ; : .

Задача 5

В ромбе уравнения двух сторон заданы уравнениями: и

. Диагонали пересекаются в точке N (5;5). Составить уравнения

двух других сторон ромб . Найти площадь ромба

Дано:

-ромб

,

,

- точка пересечения диагоналей

Составить уравнения сторон, найти площадь.

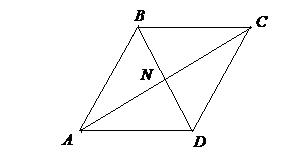
Рис.5

Решение

1 Найдем координаты точки

получим ,

2 Найдем координаты точки

Т.к диагонали ромба в точке пересечения уделяться пополам, то

, откуда ,

, откуда ,

.

3 Составим уравнение стороны АD:

Найдем из её общего уравнения : , тогда .

Воспользуемся уравнением «пучка»

4 Составим уравнение стороны СD:

Воспользуемся аналогичным алгоритмом, получим:

5 Найдем площадь ромба

Воспользуемся формулой (*)

5.1 Найдем длину диагонали ВD: ,

Воспользуемся формулой вычисления длины отрезка

5.2 Найдем координаты точек А и С:

получим ,

получим ,

5.3 Найдем длину АС

5.4 Найдем площадь ромба

Подставим длины АС и ВД в формулу (*)

(кв. ед)

Ответ: , , 24 кв.ед.

Задача 6

В прямоугольнике АВСD сторона CD задана уравнением , вершина

В (3;7), диагонали пересекаются в точке L(5;2). Найти площадь прямоугольника

Дано:

АВСD – прямоугольник,

CD: , В (3;7),

, L(5;2).

Найти площадь прямоугольника

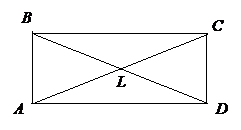
Рис.6

Решение

1 Составим уравнение ВС (рис.6)

Т.к по условию АВСD – прямоугольник, то .

Найдем из общего уравнения прямой CD - : ,тогда

Воспользуемся уравнением «пучка»:

2 Найдем точку D

Т.к диагонали прямоугольника в точке пересечения делятся пополам, то

3Найдем длины сторон

4 Найдем площадь прямоугольника:

Ответ: 42 кв.ед.

Задача 7

Равнобедренная трапеция с основаниями 10 и 4 единиц имеет острый угол 30⁰.

Написать уравнения сторон трапеции, приняв за ось ОХ меньшее основание трапеции,

а за ось ОУ ось симметрии трапеции

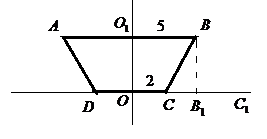
Рис.7

Замечание. К задаче 3 удобнее записать краткие условия после выполнения чертежа

Дано:

АВСD –равнобедренная трапеция,

DC – меньшее основание, ось ОУ – ось симметрии трапеции

Составить уравнения сторон

Решение

1Составим уравнение стороны DC (рис.7)

тогда DC определяется уравнением

2 Составим уравнение стороны СВ

Т.к по условию трапеция равнобедренная, то , тогда (рис.7)

(углы равны как внутренние на крест лежащие), следовательно .

По условию ОУ ось симметрии трапеции, тогда

Воспользуемся уравнением «пучка»

3 Составим уравнение стороны АD

По условию трапеция равнобедренная, то , тогда (рис.3), следовательно

По условию ОУ ось симметрии трапеции, тогда ,т.к. направление отрицательное.

Воспользуемся уравнением «пучка»

4 Составим уравнение стороны АВ

4.1 Найдем координаты точки В:

по условию ОУ ось симметрии трапеции, тогда проекция на ось ОХ

(рис.7) равна 5, тогда .

Точка В лежит на прямой СВ, её координаты удовлетворяют уравнению СВ:

4.2 Составим уравнение стороны АВ:

Воспользуемся уравнением «пучка»

Ответ:

Задача 8

Найти проекцию точки на прямую, проходящую через точку и отсекающую на осях координат равные отрезки.

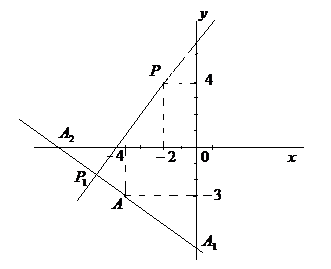
Рис.9

Решение

1 Составим уравнение прямой (рис.9)

Т.к. по условию прямая отсекает на осях координат равные отрезки,

воспользуемся уравнений прямой в «отрезках». Пусть , тогда

(*)

Точка А(-4;-3) лежит на прямой , значит её координаты удовлетворяют уравнению (*)

,

Откуда найдем:

Подставим в уравнение (*)

(**)

2 Составим уравнение (рис.9)



Из уравнения (**) имеем: , тогда

Воспользуемся уравнением «пучка»

3 Найдем

Ответ:

Приложение А

Основные уравнения прямой на плоскости