4 Средние индексы

Наряду с агрегатными индексами в статистике применяются средневзвешенные индексы. Их исчисляют в случаях, когда имеющаяся информация не позволяет рассчитать общий агрегатный индекс.

Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов. Агрегатный индекс является основной формой общего индекса, поэтому средний индекс должен быть тождественен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.

Например, при наличии данных о стоимости проданной продукции в отчетном периоде и индивидуальных индексах цен на продукцию общий индекс цен может быть рассчитан по формуле среднего гармонического индекса цен:

,

(8.7)

где .

Данное тождество получается в результате преобразования, заключающегося в том, что в значение p₀q₁ вместо p₀ подставляется p₁ на основе формулы расчета индивидуального индекса цен:

p₁ : i_p=p₀

Таким образом, общий индекс цен в среднегармонической форме тождественен общему индексу цен в агрегатной форме, т.е.

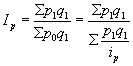
Формулы для расчета средних индексов отдельных показателей приведены в табл. 8.1., гр. 4.

Для иллюстрации расчета среднего гармонического индекса используем данные, приведенные в таблице 8.3.

Таблица 8.3 - Данные о реализации и ценах по товарной группе

Товар	Реализовано в отчетном периоде, тыс. руб.	Изменение цен в отчетном периоде по сравнению с базисным, %
А	662,5	40
Б	221,0	20
В	748,5	Без изменения

Данные последней графы таблицы отражают изменение индивидуальных индексов цен, которые по товарам А, Б, В соответственно равны 1.4, 1.2, 1.0

и т.д.

С учетом этого получим:

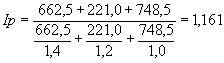или 161,1%

Цены по данной товарной группе в среднем возросли на 16,1%.

При наличии данных о стоимости продукции в базисном периоде и индивидуальных индексах физического объема товарооборота общий индекс физического объема товарооборота может быть исчислен по формуле среднего арифметического индекса:

,

(8.8)

где i_qq₀p₀= q₁p₀.

Данное тождество получается в результате преобразования, заключающегося в том, что в значение q₁p₀ вместо q₁ подставляется q₀ на основе формулы расчета индивидуального индекса физического объема продукции:

i_q·q₀=q₁

Таким образом, общий индекс физического объема продукции в среднеарифметической форме тождественен данному индексу в агрегатной форме, т.е.

Рассмотрим на примере данных приведенных в таблице 8.4. расчет среднего арифметического индекса.

Таблица 8.4 - Данные о реализации товаров в натуральном и стоимостном выражениях

Товар	Реализовано в базисном периоде, тыс. руб.	Изменение физического объема реализации в отчетном периоде по сравнению с базисным, %
А	20	20
Б	70	-2
В	55	5

Индивидуальные индексы физического объема будут равны соответственно 1,2, 0,98, 1,05.

С учетом этого рассчитаем среднеарифметический индекс:

или 103,7%

Физический объем реализации данных товаров в среднем увеличился на 3,7%.
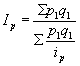