3.3.3. Регенерация теплоты в цикле гту. Многоступенчатое сжатие в компрессоре и ступенчатый подвод теплоты

Регенерация теплоты в ГТУ от газов выходящих из турбины осуществляется для подогрева воздуха подводимого в камеру сгорания, что позволяет обеспечить требуемую максимальную температуру цикла T_z. Схема ГТУ с подводом теплоты при р=const и регенерацией теплоты приведена на рис. 3.15.

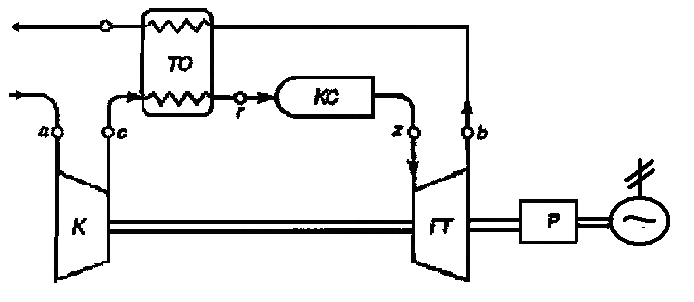
Рис. 3.15. Схема ГТД с регенерацией теплоты:

К – компрессор; ТО – теплообменник; КС – камера сгорания;

ГТ – газовая турбина; Р – редуктор

В эту схему вводится теплообменник (ТО), в котором выходящие из турбины газы подогревают воздух, поступающий из компрессора в камеру сгорания. Термодинамический цикл такой ГТУ показан на рис. 3.16.

а) б)

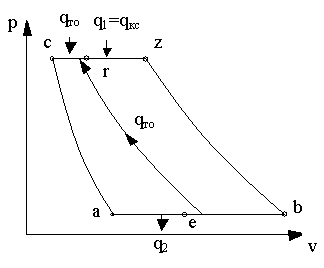
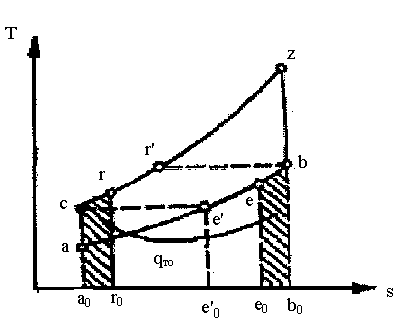
Рис. 3.16. Термодинамический цикл ГТД с регенерацией теплоты:

а – в координатах pv; b – в координатах Ts

Цикл образует следующие процессы: а-с – адиабатное сжатие; c-r – изобарный подвод теплоты q_то в теплообменнике, r-z – изобарный подвод теплоты q₁ в камере сгорания, z-b – адиабатное расширение в турбине, b-e –изобарный отвод теплоты q_то от продуктов сгорания в теплообменнике, e-a – изобарный отвод теплоты q₂ в окружающую среду.

Количество теплоты, отдаваемое газом в теплообменнике и получаемое воздухом, соответствует площадям e₀-e-b-b₀-e₀ = a₀-c-r-r₀-a₀ и определяется по формулам

. (3.27)

Для оценки эффекта регенерации вводится степень регенерации, представляющей отношение значений действительного повышения температуры воздуха в теплообменнике (T_r – T_c) к максимально возможному

. (3.28)

С целью увеличения термодинамического КПД и достижения степени регенерации теплоты близкого к единице ( ) применяется регенеративный цикл с многоступенчатым сжатием воздуха и многоступенчатым расширением газа в турбинах.

Вопросы для самопроверки

1. Изобразите принципиальную схему ГТУ без регенерации и с регенерацией теплоты.

2. Какими методами можно повысить термический КПД ГТУ?

3. Покажите графически в координатах T, s, что использование регенерации теплоты, ступенчатого сжатия и подвода теплоты приближает термический КПД цикла ГТУ к термическому КПД цикла Карно в том же интервале температур.

4. Почему в идеальном цикле ГТУ отвод теплоты принимается изобарным?

3.4. Циклы реактивных двигателей

Схема, цикл и термический КПД прямоточного

И турбореактивного двигателей

По теме не предусмотрены контрольные работы и лабораторные работы.

После изучения теоретического материалы следует ответить на вопросы для самопроверки по этой теме. Ответы можно найти в учебниках [1,3].

Реактивными называются двигатели, развивающие силу тяги за счет реакции потока газообразных продуктов сгорания, вытекающих с большой скоростью из сопла в окружающую среду. Эти двигатели применяются на летательных аппаратах и подразделяются на воздушно-реактивные двигатели, у которых окислителем топлива является кислород атмосферного воздуха, жидкостные реактивные двигатели, у которых окислителем является жидкость, запасенная на борту летательного аппарата (жидкий кислород, перекись водорода, азотная кислота), и пороховые двигатели, в которых топливом служит твердое топливо – порох, содержащий в своем составе необходимый для горения кислород.

Топливом для воздушно-реактивных двигателей служит обычно керосин, для жидкостных – водород и соединения его с углеродом, а также твердые металлы с малой атомной массой (литий, бор) и их соединения с водородом.

Наиболее просто устроен бескомпрессорный прямоточный воздушно-реактивный двигатель, который вообще не имеет движущихся частей (рис.3.17). Он состоит из диффузора 1, камеры сгорания 2 и реактивного сопла 3. При движении летательного аппарата справа налево поток набегающего воздуха тормозится в диффузоре и давление за счет снижения скорости повышается. С повышенным давлением воздух поступает в камеру сгорания, где сжигается топливо, впрыскиваемое через форсунки. Образующиеся газы выходят с большей скоростью наружу через сопло, вследствие чего образуется реактивная тяга, которая и приводит аппарат в движение.

Рис. 3.17 Рис. 3.18

Идеальный цикл такого двигателя (рис. 3.18) аналогичен циклу газотурбинной установки с подводом теплоты при p=const: адиабата 1-2 соответствует сжатию воздуха в диффузоре, изобара 2-3 – горению топлива в камере сгорания, адиабата 3-4 – расширению газов в реактивном сопле, а изобара 4-1 условно замыкает цикл.

Как уже было показано, термический КПД такого цикла определяется по формуле (3.22) при условии, что в диффузоре скорость набегающего потока w снижается до нуля (w₂=0), т.е. происходит полное адиабатное торможение. Проанализируем этот процесс в соответствии с первым законом термодинамики для потока (2.36).

.

В рассматриваемом случае ( ), при предположении, что , , последнее уравнение приобретает вид:

.

Берем интеграл с обеих частей этого уравнения

откуда получаем:

, (3.29)

где Т₁ и Т₂ –соответственно температура потока при входе в диффузор и после адиабатного торможения

Далее

; . (3.30)

Тогда формула для термического КПД примет вид:

откуда, разделив числитель и знаменатель на , получим окончательно:

. (3.31)

Полученная формула показывает, что термический КПД цикла зависит от скорости полета. Легко показать, что при из-за малой степени сжатия он получается незначительным ( 0,12). Таким образом, применение бескомпрессорных прямоточных реактивных двигателей становится целесообразным только при сверхвысоких скоростях (3000 4000 км/ч), когда степень сжатия получается достаточно большой и доходит до 0,55 - 0,65.

Чтобы повысить степень сжатия, а следовательно, и термический КПД прямоточного воздушно-реактивного двигателя при скоростях полета , характерных для современной авиации, его снабжают дополнительно турбокомпрессором, который устанавливается за диффузором и приводится в действие газовой турбиной, установленной перед реактивным соплом двигателя. Схема такого турбокомпрессорного воздушно-реактивного двигателя представлена на рис. 3.19. Она включает в себя диффузор 1, турбокомпрессор 2, камеру сгорания 3, газовую турбину 4 и реактивное сопло 5.

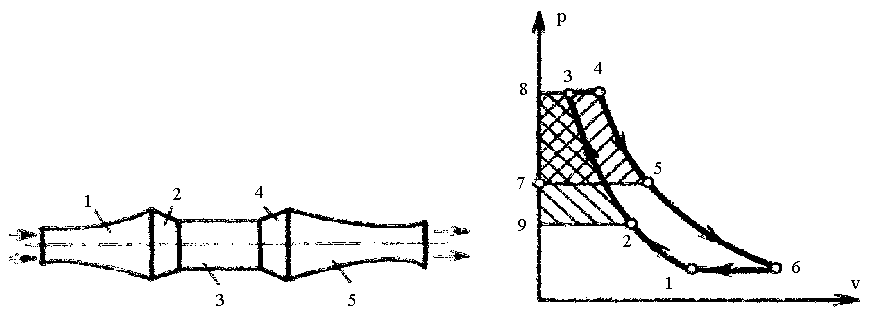
Рис. 3.19 Рис. 3.20

Идеальный цикл такого двигателя (рис. 3.20) состоит из адиабаты 1-2, соответствующей сжатию воздуха в диффузоре 1, продолжающей ее адиабаты 2-3, соответствующей дополнительному сжатию воздуха в компрессоре 2, изобары 3-4, соответствующей сгоранию топлива в камере сгорания 3, адиабата 4-5, соответствующей расширению газов в турбине 4, продолжающей ее адиабаты 5-6, соответствующей расширению газов в реактивном сопле 5, и, наконец, изобары 6-1, условно замыкающей цикл.

Работа газовой турбины l_T=h₄ – h₅ изображается площадью 4-5-7-8-4 и теоретически равна работе компрессора l_k=h₃ – h₂, изображаемой площадью 2-3-8-9-2.

Сочетание реактивного двигателя с турбокомпрессором позволяет осуществлять двигатели мощностью в 3000 л.с. и более, являющиеся основным типом двигателей в современной авиации.

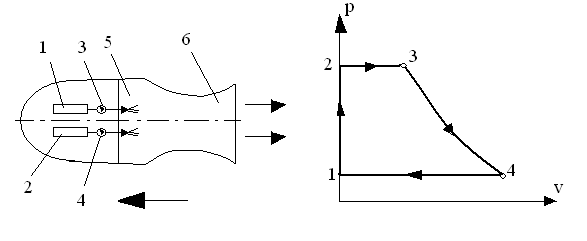
Рис. 3.21 Рис. 3.22

Жидкостные реактивные двигатели (ЖРД) в общих чертах устроены следующим образом (рис. 3.21). Топливо и жидкий окислитель подаются из баков 1 и 2 насосами 3 и 4 в камеру сгорания 5, где происходит сгорание при p=const. Газообразные продукты сгорания вытекают в окружающую среду через реактивное сопло 6, и создаваемая ими реактивная тяга толкает двигатель вперед.

Повышение давления топлива и окислителя от р₁ до р₂ осуществляется насосами, а так как жидкости практически несжимаемы, то, как показано на рис. 3.22, процесс идет по изохоре 1-2, совпадающей с осью ординат (поскольку удельный объем жидкостей очень мал и им можно пренебречь). Горению топлива соответствует изобара 2-3, расширению газов в реактивном сопле – адиабата 3-4, а смена отработавших газов топливом и окислителем – изобара 4-1, условно замыкающая цикл.

Тепло, подводимое в процессе 2-3, составляет: .

А тепло, отводимое в процессе 4-1,

следовательно,

. (3.32)

Разность энтальпии равна работе насосов, которая очень мала из-за малого удельного объема жидкостей. Поэтому величиной можно пренебречь. Тогда

. (3.33)

Вместе с тем согласно первому закону термодинамики для потока (2.36)

,

где w – скорость истечения газов из сопла. Тогда

.

Таким образом, термический КПД ЖРД возрастает пропорционально квадрату скорости газового потока, а следовательно, и квадрату скорости самого двигателя.

Жидкостные реактивные двигатели широко используются в ракетной, а в ряде случаев и в авиационной технике.

Цикл пороховых реактивных двигателей аналогичен рассмотренному и его термический КПД выражается той же формулой.