Обратимые равновесные процессы в идеальных газах

Для вывода универсальной зависимости, связывающей параметры состояния в термодинамических процессах, воспользуемся следующими уравнениями (1.27, 1.28) первого закона термодинамики и с учетом выражений (1.1, 1.9, 1.29, 1.30) напишем их в виде:

c×dT=c_v× dT + p×dv, (а) (1.31)

c× dT=c_p× dT - v×dp. (б) (1.32)

Разделив уравнение (б) на уравнение (а), найдем

. (1.33)

Введем обозначение . После интегрирования (1.33) и ряда несложных алгебраических преобразований, получаем

p·vⁿ=const. (1.34)

Последнее уравнение является уравнением политропного процесса, где n- называется показателем политропы, который меняется в пределах -¥ < n < ¥. Политропным называется процесс, в котором происходит изменение всех термодинамических функций состояния, за исключением удельной теплоемкости, которая остается постоянной величиной в течение данного процесса.

Решая зависимость относительно с, находим выражение для удельной теплоемкости политропного процесса

, (1.35)

- показатель адиабаты.

Из выражения (1.35) следует, что теплоемкость ТДС (рабочего тела) зависит от характера протекающего термодинамического процесса (на что указывает показатель политропы n) и от физических свойств рабочего тела через коэффициент показателя адиабаты k)

Рассматривая формулу (1.34) совместно с уравнением состояния p×v=R_г×T, можно представить ее еще в следующих эквивалентных формах:

T× v^n-1=const; Tⁿ× p^1-n =const. (1.36)

Изопараметрические процессы

Большое значение для теоретических исследований и решения практических задач имеют так называемые изопараметрические процессы, протекающие при постоянном (фиксированном) значении одного из параметров состояния и адиабатный процесс, который протекает без теплообмена с окружающей средой.

Термодинамические процессы удобно иллюстрировать в виде соответствующих линий (кривых) процесса на двумерных фазовых диаграммах. Широкое распространение имеют pv-, Ts-, hs-диаграммы, которые условно показаны на рис. 1.2.

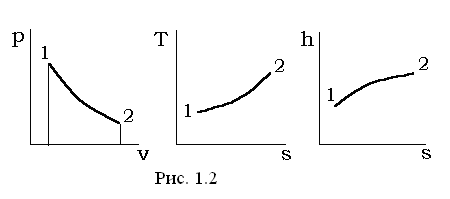
В общем случае расчет любого термодинамического процесса 1-2 при заданных начальных параметрах (p₁, v₁, T₁) должен сводиться к определению конечных параметров (p₂, v₂, T₂) состояний газа (рабочего тела) и вычислению участвующей в процессе теплоты q_1-2, изменению внутренней энергии Δu=u₂-u₁, энтальпие Δh=h₂-h₁, энтропие Δs=s₂-s₁ и работе деформации объема рабочего тела l_1-2. Таким образом, рассматриваемый процесс однозначно характеризуется значениями следующих функций процесса, параметров состояния и функций состояния:

(p₁, v₁, T₁, p₂, v₂, T₂, Δu, Δh, Δs, q_1-2, l_1-2). (1.37)

Очевидно, что перечисленный спектр величин должен быть дополнен сведениями о физической природе рабочего тела (c_p, c_v, μ_г и т.д.).

Следует отметить, что на pv-диаграмме линии процесса описываются уравнением p·vⁿ=const. (Каждому термодинамическому процессу соответствует свое значение показателя политропы n).

Определим уравнение, описывающее линии процесса на Ts-диаграмме.

Для этого рассмотрим совместно следующие выражения (1.9) и (1.2):

δq=сdT,

δq=Tds.

Учитывая равенство левых частей этих выражений, приравниваем их правые части:

сdT= Tds.

В полученном дифференциальном уравнении производим разделение переменных и осуществляем интегрирование

dT/T=ds/c , (1.38)

где T₁, s₁ – соответствуют началу процесса; с – теплоемкость рассматриваемого процесса.

Ниже приведены математические зависимости и фазовые диаграммы, необходимые для анализа и осуществления соответствующих расчетов при исследовании конкретных изопараметрических процессов.

При анализе каждого из изопараметрических процессов необходимо определить значения показателя политропы, теплоемкости процесса и изменения функций состояния, а также величину теплоты, принимающей участие в данном процессе и работу расширения, совершаемый ТДС при протекании рассматриваемого процесса.

I. Изохорный процесс v=const, dv=0.

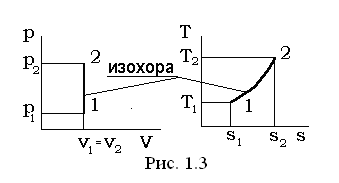
В уравнении линии процесса p×vⁿ=const, (p^1/n v=const) условие v=const удовлетворяется при n=¥, а теплоемкость изохорного процесса в соответствии с выражением равна .

Из уравнения состояния идеального газа p×v=R_г×T (при условии v=const) следует

const .

Перечень величин, представленных в выражении (1.37) в изохорном процессе, взаимосвязан следующими соотношениями:

p₁×T₂ = p₂ ×T₁; (1.39)

l_1-2= 0, v₁= v₂; (1.40)

q_1-2= u₂ - u₁; (1.41)

Δu=u₂ - u₁= c_v× (T₂ -T₁); (1.42)

Δh=h₂ - h₁=c_p× (T₂ -T₁); (1.43)

; (1.44)

. (1.45)

II. Изобарный процесс p=const, dp=0

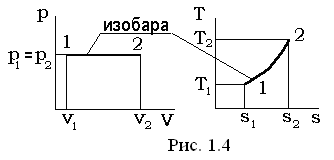
В уравнении политропного процесса p×vⁿ=const, условие р = const удовлетворяется при n = 0; теплоемкость равна .

Из уравнения состояния p×v=R_г×T (при условии p=const) следует const, .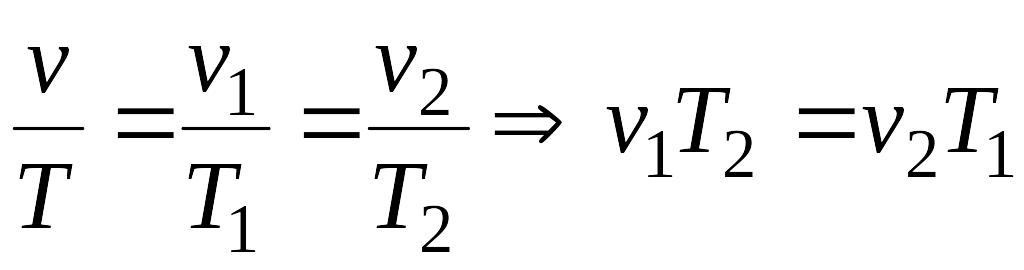

Соотношения между величинами, представленными в перечне (1.37), определяются путем интегрирования соответствующих выражений, как это производилось при рассмотрении изохорного процесса и имеют окончательный вид:

v₁×T₂= v₂× T₁; (1.46)

q_1-2= h₂ - h₁; (1.47)

l_1-2= p₁× (v₂ - v₁) = p₂× (v₂ - v₁); (1.48)

Δu=u₂ - u₁= c_v× (T₂ -T₁); (1.49)

Δh=h₂ - h₁=c_p× (T₂ -T₁); (1.50)

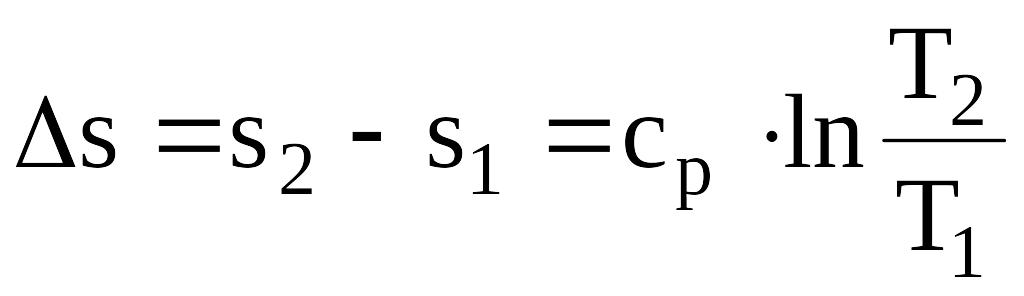. (1.51)

III. Изотермический процесс Т=const, dТ=0.

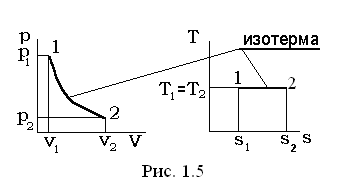
В уравнении политропного процесса T×v^n-1=const, условие Т=const удовлетворяется при n = 1, а теплоемкость для этого случая определяется из выражения .

Из уравнения состояния p×v=R_г×T (при условии T=const) следует p×v=R_г×T = const, pv = p₁ v₁ = p₂ v₂Þ p₁ v₁= p₂ v₂.

Перечень величин (1.37) в изотермическом процессе взаимосвязан следующими соотношениями:

p₁× v₁ = p₂×v₂; (1.52)

; (1.53)

q_1-2= l_1-2; (1.54)

Δu=u₂ - u₁= 0; (1.55)

Δh=h₂ - h₁=0; (1.56)

; (1.57)

T₂=T₁. (1.58)