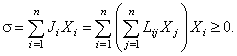22. Активный транспорт (электрогенный транспорт ионов – опыт Уссинга и ).

Активный транспорт Принцип работы АТФ-азных-насосов основан на конформационных перестройках белковой макромолекулы при взаимодействии с транспортируемым ионом.

1. Na+ - K+-насос осуществляется за счет противоградиентного переноса через мембрану трех ионов натрия из клетки и накачивающий два иона калия внутрь клетки.

1. Основные этапы Na+ - K+-насоса : образование комплекса фермента с АТФ на внутренней поверхности мембраны (эта реакция активируется ионами магния)

2. связывание комплексом трех ионов натрия

3. фосфолирирование фермента с образованием аденозинтрифосфата

4. переворот фермента внутри мембраны

5. реакция ионного обмена натрия на калий, происходящая на внешней поверхности мембраны

6. обратный переворот ферментного комплекса с переносом ионов калия внутрь клетки

7. возращение фермента в исходное состояние с освобождением ионов калия и неорганического фосфата

2. Активный транспорт ионов кальция осуществляется через мембрану саркоплазмотического ретикулума.

Ca2+ - насос идет за счет энергии гидролиза АТФ и переноса двух ионов кальция из клетки в межклеточное пространство.

• Первый этап: связывание Са2+ с комплексом Mg-АТФазы на наружной поверхности саркоплазматической мембраны.

• Второй этап: гидролиз АТФ с образованием фермент-фосфатного комплекса.

• Третий этап: переход связанного Са2+ через мембрану в клетку.

• Четвертый этап: переход кальцийсвязывающих центров на наружную поверхность мембраны

Перенос веществ через сложные мембраны можно рассмотреть на примере опыта Уссинга. Камера, заполненная нормальным раствором Рингера, разделена на две части свежеизолированной кожей лягушки. Слева - наружная поверхность кожи, справа - внутренняя серозная. Поток ионов Na+ через кожу идет от наружной к внутренней поверхности и наоборот. На коже лягушки возникает разность потенциалов: внешняя сторона имеет отрицательный заряд, внутренняя сторона имеет положительный заряд.

Уравнение Уссинга Направление и скорость диффузии зависит от концентрации градиентов. Где

Мск - поток вещества из

среды в клетку

Мкс - поток вещества из

клетки в среду

С к – концентрация

вещества в клетке

Сс – концентрация

вещества в среде

23. Понятие обобщенных сил и потоков. Соотношение взаимности Онзагера. Теорема Пригожина.

Обобщенные потоки и термодинамические силы могут быть связаны так называемыми соотношениями Онзагера. Эта связь ограничивается принципом Кюри, запрещающим взаимную связь явлений различной тензорной размерности. Обобщенные потоки У ( зависят от обобщенных сил, и наоборот - скорость химической реакции зависит от сродства, поток тепловой энергии - от разности температур. Обычно обобщенные потоки определяются предыдущей историей образца. Координаты обобщенных потоков и обобщенных термодинамических сил связаны между собой с помощью феноменологических коэффициентов. Структура обобщенных потоков является границей некоторого g с малой нормой. Если заданы обобщенные потоки через каждое отверстие, то grad ср определяется однозначно. Если заданы обобщенные потоки через каждое отверстие, то gradcp определяется однозначно. Наконец, обобщенные потоки, принадлежащие плотному замыканию класса полигональных потоков, будем называть плотными потоками, а границу такого плотного потока будем называть плотной границей. Обозначим через Q пространство плотных границ. Любой такой обобщенный поток является риссовой мерой на А, и его можно рассматривать как риссову меру на Л с носителем в А. Таким образом, g p есть замкнутый обобщенный поток в - пространстве, a g - его ограничение на множество А. Ввиду утверждения ( i) и леммы (89.3), g p является смесью единичных течений, a g - смесью их ограничений на А. Определенный подобным образом обобщенный поток является величиной, единственным образом связанной с данным отверстием. Определенный подобным образом обобщенный поток является величиной, единственным образом связанной с данным отверстием. Для того чтобы обобщенный поток gg обладал симплициальной границей Р0, необходимо и достаточно, чтобы он был пределом полигональных потоков с той же границей. Назовем сг-полигональным потоком обобщенный поток, который можно представить в виде счетной смеси отрезков. Используемое нами понятие обобщенного потока наиболее близко к эйлерову описанию движения жидкости. Однако классическая гидромеханика требует, чтобы выполнялось еще дополнительное условие, известное под названием уравнения неразрывности. В нашем случае ему соответствует ограничение, налагаемое на границу. С какими же обобщенными потоками и обобщенными силами приходится иметь дело в случае биологических открытых систем - клеток и организмов. Мы рассматриваем эти системы как химические, находящиеся при постоянной температуре. В них протекают химические реакции и происходит транспорт вещества. Допустим, что все обобщенные потоки и обобщенные силы, входящие в выражения для производства энтропии или для диссипативной функции, обращаются в нуль при достижении системой состояния с нулевым производством энтропии. Этому условию отвечает либо подлинно внутреннее равновесное состояние системы, либо такое ее стационарное состояние при наличии внешнего поля, когда перенос всех обобщенных координат прекращается, хотя система и остается неоднородной. До сих пор, изучая обобщенные потоки и их границы, мы пользовались только штрих-метрикой, которая эквивалентна слабой сходимости. Выражения для обобщенных сил и обобщенных потоков приведены в табл. 10.1. Выводы этих выражений даны ниже. Решение уравнений балансов одного типа обобщенных потоков ХТС получают в виде соотношений между базисными и свободными потоками, просуммировав в этой матрице элементы строк подматрицы [ Е ], умноженные на соответствующие свободные потоки ХТС. Теорема, ( i) Каждый замкнутый обобщенный поток является смесью единичных течений, ( и) Каждый обобщенный поток с симплициальной границей является смесью ограниченных течений, ( in) Каждый обобщенный поток с плотной границей является смесью ограниченных прерывистых течений. Наличие или отсутствие таких связей между обобщенными потоками определяется не только природой последних, но и характером линейных преобразований исходных потоков и сил к их базисам. На основе рассмотренного алгоритма расчета балансов одного-типа обобщенных потоков при решении задач первой группы пог лучают ациклический или оптимальный циклический информационный граф системы уравнений и вычисления проводят без итерационных процедур или с минимальным числом итерационных процедур. При решении задач второй группы необходимо составить. Совпадение нижних граней для полигональных и для обобщенных потоков с одинаковой симплициальной границей р можно выразить в виде теоремы замыкания, которая показывает, что такое граничное условие налагает существенные ограничения на обобщенный поток. Равенство (13.2) показывает, что в односвязном теле обобщенный поток через любой контур равен нулю. ХТС; W n - / - ый обобщенный поток, соответствующий некоторому параметру физического потока, входящего в i-ый элемент; W i - ; - ый обобщенный поток, отвечающий параметру фиктивного потока, имеющего источник в г - ом элементе; W j - / - ый обобщенный поток, соответствующий некоторому параметру выходящего из г - го элемента физического потока; W J - / - ый обобщенный поток, который отвечает параметру фиктивного потока, имеющего сток внутри г-го элемента ХТС. Интуиция подсказывает, что аналогичным способом можно описать произвольный обобщенный поток g; этого можно достичь, заменив в (66.6) а переменной точкой х, a ga - переменным обобщенным линейным элементом, проходящим через эту точку. Однако для того, чтобы получить подобное представление из риссовского, потребуется такая форма теоремы Фубини, которая редко встречается в учебниках анализа1, и поэтому мы не будем этого делать. На основе предложенного алгоритма расчета балансов одного типа обобщенных потоков при решении задач первой группы получают ациклический или оптимальный циклический информационный граф системы уравнений и вычисления проводят без итерационных процедур или с минимальным их числом. При решении задач второй группы необходимо составить дополнительные уравнения функциональных связей, которые устанавливают соотношения между неизвестными коэффициентами указанных связей, заданными значениями регламентированных потоков и внутренними потоками ХТС в зависимости от типа и параметров элементов системы. В настоящее время установлено, что требование линейной зависимости обобщенных потоков от обобщенных сил для процессов переноса не является слишком жестким. Последнее обстоятельство свидетельствует о слабой зависимости производной dJi / dXj от обобщенных сил. В противоположность этому линейные связи между плотностями скоростей wr ( V) химических реакций и их средствами Ат имеют место лишь при очень малых значениях Аг. В общем случае зависимости wr ( V) от Аг нелинейны. Подробно этот вопрос рассмотрен в гл. В настоящее время установлено, что требование линейной зависимости обобщенных потоков от обобщенных сил для процессов переноса не является слишком жестким. Последнее обстоятельство свидетельствует о слабой зависимости производной dJjdXj от обобщенных сил. В противоположность этому линейные связи между плотностями скоростей wr ( V) химических реакций и их средствами Ат имеют место лишь при очень малых значениях Аг. В общем случае зависимости wr ( v) от Аг нелинейны. Подробно этот вопрос рассмотрен в гл. Теперь распространим эту аналогию с движением жидкости и газа на произвольные обобщенные потоки. Поэтому на более высокий уровень иерархии по системе связи передается некоторый обобщенный поток информации. Исполнительными системами объекта, к которым направляется поток управляющих воздействий, могут быть различные виды автоматических устройств и систем, роботы, а также технический персонал объекта. Ясно, что такое представление может существовать только в том случае, когда обобщенный поток g по меньшей мере замкнут. Для определения материальных и тепловых нагрузок на элементы ХТС систему уравнений балансов одного вида обобщенных потоков ( IX, 1 6) дополняют уравнениями функционал ь-ныхсвязей. В приведенной записи (4.2.63) скалярные величины Jk и Xk следует рассматривать как компоненты нескольких векторов обобщенных потоков и соответствующих им векторов обобщенных термодинамических сил. Функцию с в (4.2.63) называют диссипативной. Судя по характеру сделанных приближений, коэффициенты а не зависят от обобщенных сил Xj и обобщенных потоков Jt, однако они являются, вообще говоря, функциями плотностей обобщенных координат и, следовательно, функциями обобщенных потенциалов в той или иной точке системы. Имея в виду последнее равенство, говорят, что локальная диссипа-тивная функция инвариантна относительно линейных преобразований обобщенных потоков и сил. Понятие смеги и теорему нужного нам типа для начала удобно проиллюстрировать на одном простом частном случае обобщенного потока. Кроме того, результаты, относящиеся к этому частному случаю, понадобятся нам, прежде чем мы сможем произвести дальнейшее расширение класса допустимых кривых в задачах вариационного исчисления, о котором было сказано ранее. Имея в виду последнее равенство, говорят, что локальная диссипа-тивная функция инвариантна относительно линейных преобразований обобщенных потоков и сил. Судя по характеру сделанных приближений, коэффициенты а / не зависят от обобщенных сил Xj и обобщенных потоков Jit однако они являются, вообще говоря, функциями плотностей обобщенных координат и, следовательно, функциями обобщенных потенциалов в той или иной точке системы. Теорема, ( i) Каждый замкнутый обобщенный поток является смесью единичных течений, ( и) Каждый обобщенный поток с симплициальной границей является смесью ограниченных течений, ( in) Каждый обобщенный поток с плотной границей является смесью ограниченных прерывистых течений. Эту норму назовем плотнойх) и отметим, что соответствующее понятие предела совместимо как со слабым пределом длу обобщенных потоков ( эквивалентным сходимости в штрих-метрике), так и с пределом по норме для их границ. Плотными назовем также соответствующие метрику, топологию, предел и замыкание. Уравнение ( 11 70) является основой предложенного формального метода составления и расчета систем уравнений балансов одного типа обобщенных потоков ХТС. Рассмотрим общий вид уравнений функциональных связей, которые при расчете материальных и тепловых балансов ХТС дополняют системы уравнений балансов обобщенных потоков. За основу при описании явления электропроводности возьмем выражение для плотности диссипативной функции системы (4.11.11), которое предопределяет энергетический вариант выбора обобщенных потоков и сил. Уравнение ( 11 70) является основой предложенного фор - - мального метода составления и расчета систем уравнений балансов одного типа обобщенных потоков ХТС. В состоянии полного равновесия системы ( напомним, что система находится в полном равновесии, если она термодинамически равновесна и неподвижна) все обобщенные потоки и все обобщенные силы равняются нулю. При описании процессов переноса обобщенных координат с помощью феноменологических законов (1.28.5) следует иметь в виду, что линейные зависимости могут быть и между обобщенными потоками, и между обобщенными силами. Так, согласно равенству (1.8.19), поток электрического заряда всегда является линейной комбинацией потоков масс или чисел молей компонентов системы.

В термодинамике необратимых процессов Ларс Онзагер сформулировал следующее положение: при небольших отклонениях от равновесия термодинамический поток можно представить в виде линейной комбинации термодинамических движущих сил:

(4.1)

Здесь   - движущая сила, сопряжённая с потоком  ; она определяет прямой эффект.   - движущие силы, сопряжённые с другими потоками; они характеризуют в (4.1)перекрёстные эффекты по отношению к процессу i. Коэффициенты L называют феноменологическими коэффициентами:   - при прямом эффекте,   - при перекрёстных эффектах, причём влияние прямого эффекта существенно превышает влияние перекрёстных эффектов:

     Соотношения типа (4.1) для систем, близких к равновесию, называют соотношениями взаимности Онзагера или линейными соотношениями.       С учётом (4.1) производство энтропии системы можно представить в виде квадратичной формы:

Данная квадратичная форма является положительно определённой (доказательство приводится в разделе "Характеристика производства энтропии").       Л. Онзагер также определил, что в линейных соотношениях (4.1) недиагональные коэффициенты равны [9]:

(4.2)

т.е. матрица феноменологических коэффициентов должна быть симметричной. Иными словами, если на поток  , соответствующий необратимому процессу i, действует сила  необратимого процесса j, то сила   действует на поток   с тем же коэффициентом  . Соотношения (4.2) называют принципом симметрии феноменологических коэффициентов.

Теорема Пригожина — теорема термодинамики неравновесных процессов. Согласно этой теореме, стационарному состоянию системы (в условиях, препятствующих достижению равновесного состояния) соответствует минимальное производство энтропии. Если таких препятствий нет, то производство энтропии достигает своего абсолютного минимума — нуля. Доказана И. Р. Пригожиным в 1947 из соотношений взаимности Онсагера. Теорема Пригожина справедлива, если кинетические коэффициенты в соотношениях Онсагера постоянны; для реальных систем она справедлива лишь приближённо, поэтому минимальность производства энтропии для стационарного состояния не является столь общим принципом, как максимальность энтропии для равновесного состояния.

Формулировка теоремы: В стационарном состоянии продукция энтропии внутри термодинамической системы при неизменных внешних параметрах является минимальной и константной. Если система не находится в стационарном состоянии, то она будет изменяться до тех пор, пока скорость продукции энтропии, или, иначе, диссипативная функция системы не примет наименьшего значения.