2. Модель Вольтерра
В качестве второго примера рассмотрим классическую модель взаимодействия видов, которая впервые была предложена В. Вольтерра в тридцатые годы XX века для объяснения периодических изменений числа особей, так называемую вольтерровскую модель «хищник-жертва». Более подробно модели взаимодействия видов мы рассмотрим в Лекции 9.
Пусть в некотором замкнутом районе живут хищники и жертвы, например, зайцы и волки. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Обозначим число зайцев (жертв) x, а число волков (хищников) – y. Так как количество пищи у зайцев неограниченно, мы можем предположить, что они размножаются со скоростью, пропорциональной их числу:
(5.16)
Если рождаемость зайцев превышает их смертность, 0. Выражение (5.16) соответствует автокаталитической реакции первого порядка.
Пусть убыль зайцев пропорциональна вероятности встречи зайца с волком, т.е. пропорциональна произведению численностей xy. Можно предположить по аналогии с бимолекулярными реакциями, где вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, что и количество волков нарастает тем быстрее, чем чаще происходят их встречи с зайцами, а именно, пропорционально xy.
Кроме того, имеет место процесс естественной смертности волков, причем скорость смертности пропорциональна их количеству.
Эти рассуждения приводят к системе уравнений для изменений численности зайцев-жертв x и волков-хищников y.
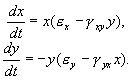(5.17)
Покажем,
что система уравнений (5.17) имеет на
фазовой плоскости переменных xy ненулевую
особую точку типа центр. Координаты
этой особой точки
легко
найти, приравняв правые части уравнений
системы (5.17) нулю. Это дает стационарные
ненулевые значения:
.
Так
как все параметры 
положительны,
точка
расположена
в положительном квадранте фазовой
плоскости. Линеаризация системы вблизи
этой точки дает:
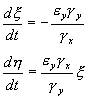(5.18)
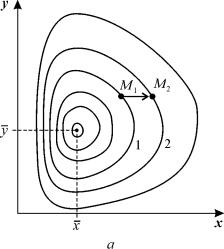
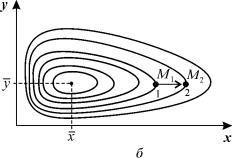
Рис. 5.3. Фазовый портрет системы 5.17. Особая точка типа «центр».
а – параметры системы: x = 4, xy = 0,3, y = yx = 0,4
б – параметры системы: x =2, xy = 0,3, y = yx = 0,4
Здесь , - отклонения численностей от их стационарных значений:
Характеристическое уравнение системы (5.18):
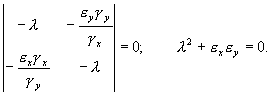
Корни этого уравнения чисто мнимые:
.
Таким образом, исследование системы показывает, что траектории вблизи особой точки являются концентрическими эллипсами, а сама особая точка – центром. Расcматриваемая модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной, и определяется параметрами системы (рис. 5.3).
Изменения численности жертвы и хищника во времени представляют собой колебания, причем колебания численности хищника отстают по фазе от колебаний жертв.
Как мы уже отмечали в Лекции 4, особая точка типа центр устойчива по Ляпунову, но не асимптотически. Покажем на данном примере, в чем это проявляется. Пусть колебания x(t) и y(t) происходят таким образом, что изображающая точка движется по фазовой траектории 1 (рис 5.3).
В момент, когда точка находится в положении М1, в систему добавляется извне некоторое число особей y такое, что изображающая точка переходит скачком из точки M1 в точку M2 . Если после этого систему предоставить самой себе, колебания x(t), y(t) уже будут происходить с большими амплитудами, чем прежде, и изображающая точка будет двигаться по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии.
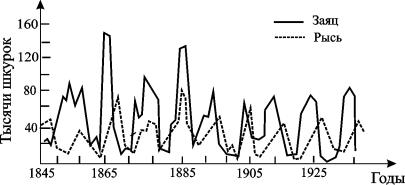
Рис. 5.4. Кривые численности зайца и рыси в Канаде