1. Кинетические уравнения Лотки (a.J. Lotka. Elements of Physical Biology, 1925)

Лоткой была исследована гипотетическая химическая реакция:

 

 

Модель очень простая и служит хорошей иллюстрацией применения исследования устойчивости стационарного состояния системы методом линеаризации.

Пусть в некотором объеме находится в избытке вещество А. Молекулы А с некоторой постоянной скоростью   превращаются в молекулы вещества X (реакция нулевого порядка). Вещество Xможет превращаться в вещество Y, причем скорость этой реакции тем больше, чем больше концентрация вещества Y – реакция второго порядка. В схеме это отражено обратной стрелкой над символом Y. Молекулы Y в свою очередь необратимо распадаются, в результате образуется вещество B (реакция первого порядка).

Запишем систему уравнений, описывающих реакцию:

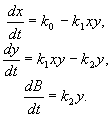                                           (5.13)

Здесь x, y, B - концентрации химических компонентов. Первые два уравнения этой системы не зависят от B, поэтому их можно рассматривать отдельно. Рассмотрим стационарное решение системы:

Из этих условий получим систему алгебраических уравнений, связывающих равновесные концентрации :

                                         (5.14)

Координаты особой точки:

.

Исследуем устойчивость этого стационарного состояния методом Ляпунова. Введем новые переменные , , характеризующие отклонения переменных от равновесных концентраций :

.

Линеаризованная система в новых переменных имеет вид:

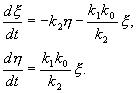                                     (5.15)

Отметим, что величины отклонений от стационарных значений переменных ,  могут менять знак, в то время как исходные переменные x, y, являющиеся концентрациями, могут быть только положительными.

Запишем характеристическое уравнение системы (4.3):

 

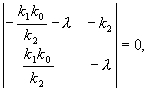
или

.

Корни характеристического уравнения:

.

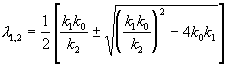Фазовый портрет системы (5.13) изображен на рис. 5.1.

 

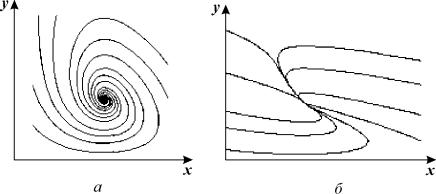
Рис. 5.1. Фазовый портрет системы 5.13.

а – устойчивый фокус, 

б – устойчивый узел. 

 

При   подкоренное выражение отрицательно, и особая точка – фокус, при обратном соотношении – узел. И в том и в другом случае особая точка устойчива, так как действительная часть обоих корней характеристического уравнения отрицательна.

Таким образом, в описанной выше химической реакции возможны разные режимы изменения переменных в зависимости от соотношения величин констант скоростей. Если  , имеют место затухающие колебания концентраций компонентов, при   – бесколебательное приближение концентраций к стационарным.

 

 

Рис. 5.2 Плоскость параметров для системы 5.14. а – область устойчивого фокуса; б– область устойчивого узла

 

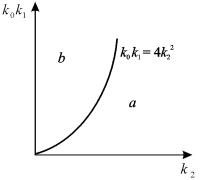
Соотношение параметров   соответствует изменению типа особой точки системы уравнений (5.13).

Рассмотрим плоскость параметров, где по оси абсцисс отложены значения константы k₂, а по оси ординат – произведение k₀ k₁. Парабола k₀ k₁ = 4 k²₂ делит изображенную на рис. 5.2 плоскость параметров на две области – устойчивых узлов и устойчивых фокусов. Задавая те или иные значения параметров, можно получить колебательный и бесколебательный режимы изменения концентраций веществ x и y, и фазовый портрет системы, соответственно, будет собой представлять фокус (а) или узел (б), изображенные соответственно на рис 5.1а, и 5.1б.

Если в системе установятся стационарные концентрации веществ x и y, это приведет к установлению постоянной скорости прироста концентрации вещества В в третьем уравнении системы (5.13):

.

Ясно, что в действительности такая система реализоваться не может, так как в ней при t    концентрация вещества В стремится к бесконечности. Однако система, подобная системе реакций Лотки, может представлять собой фрагмент более сложной химической системы. Исследованные нами уравнения правильно описывают поведение компонентов x и y, если приток вещества x (скорость его постоянна и равна k₀) осуществляется из большого «резервуара», а отток вещества y – в большой «резервуар» (значение В очень велико). При этих предположениях на малых промежутках времени (по сравнению с временем существенного изменения заполненности емкости B) наше рассмотрение является вполне правомерным.