Движение частицы в однородном электрическом поле

При движении сферической частицы из состояния покоя под действием постоянных внешних сил при Re < 0,5 уравнение движения запишется в виде:

, (2.30)

где F = Eq + mg  внешние силы, определяемые воздействием электрического и гравитационного полей.

Если заряд частицы и напряженность поля неизменны, то решение уравнения имеет вид:

,

где _уст= F/(6a)  установившаяся скорость движения частицы;  = m/(6a)  постоянная времени, определяющая характерное время изменения скорости частицы.

Постоянная времени связана с длиной инерционного пробега частицы  l_и. Если частица имеет начальную скорость ₀, то при отсутствии воздействия внешних сил до полной остановки своего движения она пройдет путь, равный:

.

Чем больше проявляется влияние инерционных свойств частицы, тем больше длина инерционного пробега.

Для расчета движения частиц при Re  0,5 можно воспользоваться линейной аппроксимацией силы сопротивления среды в виде (2.29). Тогда реше­ние записывается по аналогии с решением уравнения (2.30). Более сложный для расчета случай имеет место, когда заряд частиц и напряженность поля в про­цессе движения изменяются. Аналитическое решение для этого случая отсутст­вует.

Более просто решается задача, если силами инерции при расчете можно пренебречь. Возможность такого упрощения определяется числом Стокса.

Число Стокса представляет собой отношение длины инерционного пробега частицы при скорости _x к характерному размеру l  расстоянию, на кото­ром действующая на частицу внешняя сила претерпевает изменение, соизмери­мое с ее средним значением:

(2.31)

Под характерной скоростью понимается скорость, определяемая действием внешних сил без учета сил инерции.

Таким образом, число Стокса определяет влияние сил инерции на движение частицы под действием переменной внешней силы. Если St << 1, то движе­ние частицы можно считать безынерционным.

По аналогии с понятием подвижности ионов можно ввести понятие подвижности частицы:

, (2.32)

здесь .

Таким образом, подвижность частицы, обладающей зарядом q, представляет собой установившуюся скорость движения в поле единичной напряженно­сти.

Для случая, когда частица приобретает заряд в поле коронного разряда, можно построить зависимость подвижности от размера частиц (рис. 2.9).

Рис. 2.9. Зависимость подвижности B_q от радиуса частиц

1  Е = 1кВ/см; 2  Е = 3 кВ/см

Подвижность имеет минимум при размере частиц 2а равном 0,3  0,5 мкм. Возрастание подвижности для частиц очень малого размера объясняется уменьшением силы сопротивления среды из-за того, что размер час­тиц становиться соизмеримым с длиной свободного пробега молекул воздуха (поправка Кенингема).

Возрастание подвижности для частиц 2а  1мкм объясняется тем, что начинает работать механизм «ударной» зарядки и имеет место квадратичный ха­рактер зависимости заряда от размера частиц. Тогда в соответствии с (2.31) подвижность растет пропорционально размеру частиц.

Для расчета силы сопротивления среды движению частиц несферической формы используется замена на эллипсоид, эквивалентный частице по объему и соотношению осей. В литературе имеются данные по коэффициенту сопротивления для эллипсоидов.

При движении, начиная с переходного значения Re, частицы приобре­тают определенную ориентацию (за счет гидродинамического взаимодействия с окружающей средой). Ориентация такова, что частица при движении испытывает максимальное сопротивление. Например, на цилиндрическую удлиненную частицу при движении в воздушной среде в электрическом поле действуют два вращающих момента (рис. 2.10).

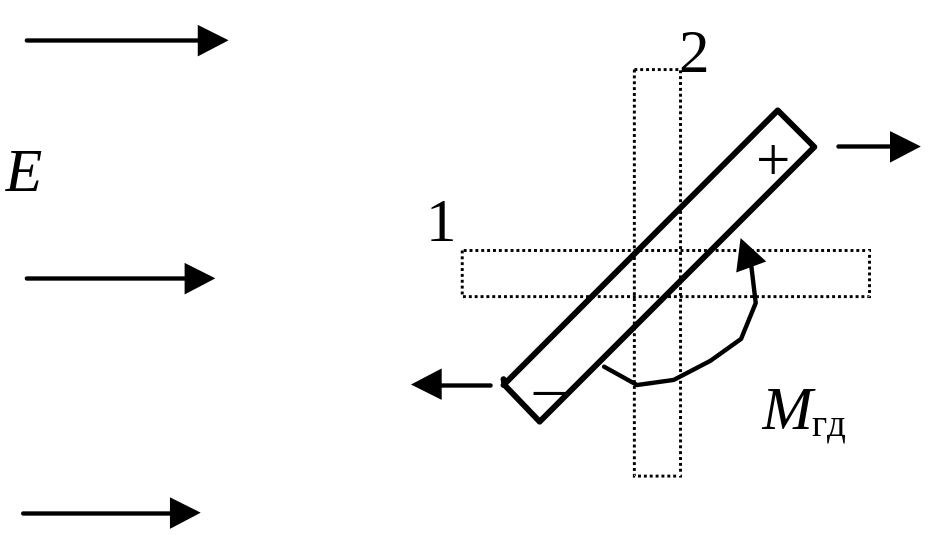
Рис.2.10. Силы, действующие на частицу

несферичной формы

С одной стороны электрическое поле стремится развернуть поляризованную частицу таким образом, чтобы она расположилась своей большой осью вдоль силовых линий электрического поля (положение 1). С другой стороны гидродинамические силы сопротивления среды движению частицы  М_гд  стремится развернуть ее таким образом, чтобы лобовое сопротивление было максимальным из всех возможных положений частицы, то есть перпендику­лярно направлению движения частицы под действием сил электрического поля. В результате может устанавливаться некоторая промежуточная ориентация частицы в электрическом поле, как показано на рис. 2.10.