Методические указания по обработке результатов измерений

Результат измерения Х состоит из действительного значения из­меряемой величины Х_Д и погрешности измерения Δ:

Х = Х_Д + Δ

В общем случае Δ состоит из систематической Δcис и случайной Δ_СЛ составляющих погрешности.

При обработке результатов измерений различают прямые и косвенные, однократные и многократные измерения.

Обработка результатов прямых однократных измерении

Однократные измерения проводятся только при отсутствии случайной составляющей погрешности, поэтому при однократных измерениях оцени­вается только систематическая погрешность Δcис .

Систематическая погрешность измерения складывается из трех соста­вляющих: основной инструментальной Δ_ОСН, дополнительной инструмен­тальной Δ_ДОП и методической погрешности Δ_М.

Определение основной инструментальной погрешности.

Основная инструментальная погрешность определяется по классу точности прибора.

Если класс точности представлен в виде предела приведенной погреш­ности (обозначен на приборе десятичным числом с точкой) как:

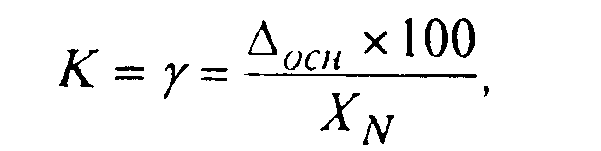где К - класс точности прибора,

Х_N - нормирующее значение, то

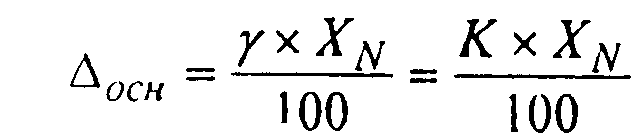(2.1)

Если класс точности прибора представлен в виде отношения c/d , то в относительном виде основную инструментальную погрешность измерения

_осн можно определить по выражению:

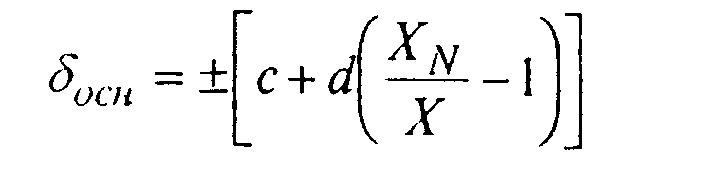(2.2)

где Х _N - конечное значение диапазона измерения прибора,

Х - измеряемое значение.

В абсолютном виде основную инструментальную погрешность Δ_осн можно определить по выражению:

Δ_осн = (2.3)

Определение дополнительной инструментальной погрешности Дополнительная инструментальная погрешность также связана с клас­сом точности прибора и выражается в той же форме, что и основная погрешность.

Измерение показаний электроизмерительного прибора класса точности, вызванное γ изменением температуры окружающей среды, не должно выходить за пределы γ % на каждые 10° С изменения температуры в пределах рабочего интервала температур (для расчета дополнительной инструментальной погрешности).

Например, изменение показаний электроизмерительного прибора класса 0,5, вызванное изменением температуры окружающей среды, не дол­жно выходить за пределы 0,5% на каждые 10°С изменения температуры в пределах рабочего интервала температур,

Конкретная связь дополнительной погрешности с классом точности раскрывается в частных стандартах на средства измерения.

Для цифровых приборов (класс точности которых задается в виде c/d) дополнительная инструментальная погрешность _доп, вызванная изменением температуры на Δt градусов относительно нормальной (20⁰ С) и выраженная в процентах, не превышает значения:

, (2.4)

а абсолютная не превышает значения:

.

Определение методической погрешности

Методическая погрешность возникает из-за несовершенства метода измерения, из-за влияния средств измерения на объект, свойство которого

измеряется, т.е. в каждом конкретном случае методическая погрешность оценивается по-своему.

Так при измерении тока в цепи амперметром, включаемым в цепь во время измерения, методическая погрешность возникает из-за изменения тока

при включении амперметра с внутренним сопротивлением R_А в цепь с сопротивлением R за счет изменения общего сопротивления.

Для приведенного примера действительный ток, протекающий в цепи без амперметра I₀= U/R , при наличии амперметра измеряется ток:

I = U/(R+R_A)

Абсолютная методическая погрешность:

относительная методическая погрешность:

(2.5)

Возникающая погрешность - методическая - при правильно поставленном измерении должна быть незначительной. В приведенном примере методическая погрешность тем меньше, чем меньше внутреннее сопротивление амперметра R_А по сравнению с сопротивлением цепи R.

Суммирование погрешностей.

Согласно ГОСТ 8.207-76 суммарная систематическая погрешность измерения определяется по выражению:

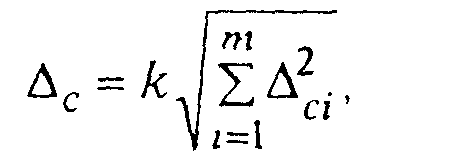(2.6)

где Δ _ci - i-я составляющая систематической погрешности,

т- число составляющих систематической погрешности,

k- коэффициент, зависящий от заданной доверительной вероятности Р.

При доверительной вероятности Р = 0,95 коэффициент k принимают равным 1.1.

Запись результата измерения

Результат измерения представляется в виде: Хд =Х + Δ _c , Р = 0,95.

Обработка результатов прямых многократных измерений

Многократные измерения проводятся при наличии как систематической, так и случайной составляющей погрешности и при возможности получения результата с грубыми погрешностями (промахами). При обработке многократных наблюдений исключаются грубые погрешности и уменьшается в раз случайная погрешность Δ_сл измерения ( n-число измерений).

Обработка результатов многократных измерений складывается из

следующих этапов:

- оценивание систематической составляющей погрешности;

- исключение из ряда измерений результатов с грубыми погрешностями

- оценивание случайной составляющей погрешности;

- определение результата измерения и его суммарной погрешности;

Оценивание систематической составляющей погрешности.

Значение систематической составляющей погрешности не зависит от числа проведенных измерений и определяется аналогично как и при прямых однократных измерениях.

Исключение из ряда измерений результатов с грубыми погрешностями

Выделить грубые ошибки (промахи) из результатов многократных измерений Х₁ Х_2, … Хn можно с помощью критерия Груббса-Смирнова. Порядок проверки с помощью этого критерия следующий:

1. Определить по результатам измерения среднее значение и оценку среднего квадратичного отклонения (дисперсии):

= (2.7) ; , при n 20; (2.8)

2. Выделить из результатов измерения минимальное X_min максимальное X_max значения и вычислить отношения V₁ и V₂

V₁=(X_max - )/ ; (2.9) V₂=( - X_min)/ . (2.10)

3. По таблице 2 приложения (Распределение случайных величин Груббса-Смирнова) найти граничное значение β_гр по вероятности Р=0.95 и объему выборки n .

4. Проверить выполнение неравенств

; (2.11) ( 2.12)

Если неравенства (2.11) и (2.12) выполняются, то нет оснований считать X_min и X_max резко выделяющимися наблюдениями. Если не выполняется неравенство (11), то X_max нужно исключить из дальнейшего рассмотрения; если не

выполняется неравенство (12), то нужно исключить X_min.

При исключении из рассмотрения хотя бы одного результата измерения проверку повторить без исключенного значения Хi.