Приклади перевірки сумісності сукупності тверджень

Розглянемо таку сукупність тверджень.

Якщо єдиноріг – міфічна тварина, то він безсмертний, а якщо не міфічна, то він – смертний ссавець. Якщо єдиноріг або безсмертний, або є ссавцем, то він озброєний рогом. Єдиноріг є міфічною твариною, якщо він озброєний рогом.

Перевіримо сумісність цих тверджень, тобто перевіримо, чи можуть ці твердження бути одночасно істинними. Використаємо для цього формальні методи, описані вище.

Для перекладу речень на мову логіки висловлень уведемо наступні літери:

А – єдиноріг є міфічною твариною;

В – єдиноріг – безсмертний;

С – єдиноріг є смертним ссавцем;

D – єдиноріг озброєний рогом.

Отже, подаємо дані твердження у вигляді формул:

A  B, A  C, (B  C)  D, D  A.

Сукупність тверджень буде сумісною, якщо ці формули мають спільну модель, або формула F= (A  B)  (A  C)  ((B  C)  D)  ( D  A) має хоча б одну модель, тобто є несуперечливою. Отже, застосувавши описані вище методи для перевірки суперечності формули F, дістанемо відповідь.

Перевіримо суперечність формули F за допомогою таблиць істинності. Будуватимемо інтерпретації формули F й обчислюватимемо істинносне значення формули F при кожній інтерпретації. Якщо знайдеться інтерпретація, при якій F приймає значення 1, то F несуперечна, а тоді можна зробити висновок, що подана сукупність тверджень сумісна. Інтерпретації й результати обчислень подамо у вигляді таблиці.

A	B	C	D	AB	AC	(BC)D	DA	F
0 0 0 0 0 0 0 0 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0	0 1 0 1 0 1 0 1 0 1 0 1 0 1	1 1 1 1 1 1 1 1 0 0 0 0 1 1	0 0 1 1 0 0 1 1 1 1 1 1 1 1	1 1 0 1 0 1 0 1 1 1 0 1 0 1	1 0 1 0 1 0 1 0 1 1 1 1 1 1	0 0 0 0 0 0 0 0 0 0 0 0 0 1

Таким чином, знайдено інтерпретацію І (І(A)=I(B)=I(D)=1, I(C)=0), при якій формула F приймає значення 1, отже, F несуперечна, а подана сукупність тверджень сумісна.

Розглянемо далі, як перевірити несуперечність F шляхом побудови ДНФ. Побудову ДНФ будемо здійснювати, використовуючи наведені вище співвідношення.

Маємо:

F = (A  B)  (A  C)  ((B  C)  D)  ( D  A).

Вилучимо входження зв’язки  (за допомогою тотожності F₁F₂=F₁F₂):

F = (A  B)  (A  C)  ( (B  C)  D)  (D  A).

Зменшимо область дії заперечення (за допомогою тотожності Ø(F₁F₂)= ØF₁ØF₂):

F = (A  B)  (A  C)  ((B  C)  D)  (D  A).

Застосуємо закони комутативності та асоціативності:

F = (A  B)  ((B  C)  D)  ((A  C) (A  D)).

До підформули ((A  C) (A  D)) застосуємо закон дистрибутивності:

F = (A  B)  ((B  C)  D)  (A  (C  D)).

Застосуємо закон дистрибутивності (F₁  (F₂  F₃) = (F₁  F₂)  (F₁  F₃)) до ((B  C)  D)  (A  (C  D)) (тут F₁=(B  C)  D, F₂ = А, F₃= C  D):

F = (A  B)  ((B  C)  D)  A)  ((B  C)  D)  (C  D).

Розглянемо підформулу ((B  C)  D)  A). За законом дистрибутивності

((B  C)  D)  A) = (B  C  A)  (D  A).

Розглянемо підформулу ((BC)D)(CD). За законом дистрибутивності

((B  C)  D)  (C  D) = (B  C  C  D)  (D  C  D).

Застосуємо послідовно тотожності F₁F₁=0 та F₁0=0. Маємо:

B  C  C  D = B  (C  C)  D = B  0  D = 0,

D  C  D = C  (D  D) =С  0 = 0.

Отже,

F = (A  B)  ((B  C  A)  (D  A))  (0  0)).

Застосуємо двічі тотожність F₁0= F₁. Маємо:

F = (A  B)  ((B  C  A)  (D  A)).

За законом дистрибутивності (F₁  (F₂  F₃)=(F₁  F₂)  (F₁  F₃)), де F₁=AB, F₂=B  C  A, F₃= D  A, маємо:

F = ((A  B)  (B  C  A))  ((A  B)  (D  A)).

Знову застосуємо закон дистрибутивності (до підформули ((A  B)  (B  C  A)) та до підформули ((A  B)  (D  A))). Маємо:

F = (A  (B  C  A))  (B  (B  C  A)) (A  (D  A))  (B  (D  A)).

Виконаємо спрощення АА=0, ВВ=0, а потім застосуємо F₁0=0:

F = 0  0 0  (B  (D  A)).

Застосувавши тотожність F₁0=F₁, маємо:

F = B  D  A.

Отже, побудовано ДНФ формули (A  B)(A  C)((B  C)  D)( D  A).

Зауважимо, що побудова ДНФ формули F може бути здійснена не єдиним чином. Розглянемо інший спосіб приведення F до диз’юнктивної нормальної форми.

Отже, маємо: F = (A  B)  (A  C)  ((B  C)  D)  ( D  A).

Вилучаємо входження імплікацій:

F = (A  B)  (A  C)  ( (B  C)  D)  (D  A).

Вносимо заперечення у дужки:

F = (A  B)  (A  C)  ((B  C)  D)  (D  A).

До підформули ((B  C)  D) застосуємо закон дистрибутивності:

F = (A  B)  (A  C)  (B  D)  (C  D)  (D  A).

За законами комутативності та асоціативності маємо:

F = (A  B)  (B  D)  (C  D)  ((A  C)  (D  A)).

Застосуємо закон дистрибутивності, де F₁ = (A  C), F₂ = D, F₃=А:

F = (A  B)  (B  D)  (C  D)  (((A  C)  D)  ((A  C)  A)).

За правилом поглинання (A  C)  A = А, а також за законом дистрибутивності (A  C)  D = (A  D)  (C  D) тому

F = (A  B)  (B  D)  (C  D)  ((A  D)  (C  D)  A).

Застосувавши правило поглинання (A  D)  A = А, отримаємо

F = (A  B)  (B  D)  (C  D)  ((C  D)  A).

Застосуємо закон дистрибутивності до підформули (C  D)  ((C  D)  A):

F = (A  B)  (B  D)  (((C  D)  (C  D))  ((C  D)  A)).

Перетворимо формулу (C  D) за законом F₁F₂=(F₁F₂):

F = (A  B)  (B  D)  (((C  D)  (C  D))  ((C  D)  A)).

Згідно правила F  F = 0 маємо: (C  D)  (C  D)=0. Застосуємо тотожність F₁  0 = F₁. Маємо:

F = (A  B)  (B  D)  (C  D)  A.

За законами комутативності та асоціативності маємо:

F = ((A  B)  A)  (B  D)  (C  D).

До ((A  B)  A) застосуємо закон дистрибутивності:

F = ((A  A)  (A  B))  (B  D)  (C  D).

Виконаємо спрощення (A  A) = 0, 0  (A  B) = (A  B). Тому

F = A  B  (B  D)  (C  D).

До підформули B  (B  D) застосуємо закон дистрибутивності:

F = A  ((B  B)  (B  D))  (C  D).

Оскільки (В  В) = 0, а 0  (B  D) = (B  D), то:

F = A  B  D  (C  D).

За правилом поглинання D  (C  D) = D, тому

F = A  B  D.

Остання формула є ДНФ, яка складається з одного кон’юнкта. Можна побачити, що існують дві моделі даної формули:

A=1, B=1, D=1, C=0;

A=1, B=1, D=1, C=1.

Таким чином, формула F має моделі. Отже, можна зробити висновок, що подана сукупність тверджень сумісна.

Перевіримо суперечність формули (AB)(AC)((BC)D)(DA) методом Девіса й Патнема. Для цього спочатку приведемо цю формулу до КНФ. Маємо:

F = (A  B)  (A  C)  ((B  C)  D)  (D  A).

Вилучимо входження зв’язки  (за допомогою тотожності F₁F₂=F₁F₂):

F = (A  B)  (A  C)  ( (B  C)  D)  (D  A).

Зменшимо область дії заперечення (за допомогою тотожності Ø(F₁F₂)= ØF₁ØF₂):

F = (A  B)  (A  C)  ((B  C)  D)  (D  A).

До підформули ((B  C)  D) застосуємо закон дистрибутивності:

F = (A  B)  (A  C)  (B  D)  (C  D)  (D  A).

Отже, формула F подана у КНФ. Запишемо F у вигляді множини диз’юнктів:

S = {A  B, A  C, B  D, C  D, D  A}.

У множині S немає тавтологічних диз’юнктів (отже, не застосовне правило тавтології), немає однолітерних диз’юнктів (не застосовне правило однолітерного диз’юнкту), немає чистих літер (не застосовне правило чистих літер). Єдиним застосовним до S правилом є правило розщеплення. Застосуємо це правило (вибравши за L літеру А). Маємо:

S₁={B, BD, CD}, S₂={D, C, BD, CD}.

Перевіримо суперечність множини S₁. Правило тавтології до S₁ не застосовне. Але застосовне правило однолітерного диз’юнкту (S₁ містить однолітерний диз’юнкт В). В результаті маємо множину S₃={D, CD}, до якої застосовне правило однолітерного диз’юнкту. Маємо: S₄=. Таким чином, множина диз’юнктів S₄ несуперечна, отже, й S несуперечна. А це означає, що формула F має модель. Але тоді подана сукупність тверджень сумісна.

Перевіримо суперечність формули F=(AB)(AC)((BC)D)(DA) методом резолюцій. Використаємо подання F у вигляді множини диз’юнктів S:

S = {A  B, A  C, B  D, C  D, D  A}.

Далі для зручності будемо писати диз’юнкти у стовпчик, нумеруючи їх.

1. A  B,

2. A  C,

3. B  D,

4. C  D,

5. D  A.

Побудуємо усі резольвенти диз’юнктів 1-5:

6. ВС (резольвента 1 та 2),

7. AD (резольвента 1 та 3),

8. BD (резольвента 1 та 5),

9. AD (резольвента 2 та 4),

10. BA (резольвента 3 та 5),

11. CA (резольвента 4 та 5).

Тепер побудуємо усі резольвенти диз’юнктів 1-11 (не застосовуючи, звичайно, правило резолюції до тих пар диз’юнктів, що складаються з диз’юнктів 1-5).

12. BD (резольвента 1 та 9),

13. BB (резольвента 1 та 10),

14. AA (резольвента 1 та 10),

15. BC (резольвента 1 та 11),

16. CD (резольвента 2 та 7),

17. A (резольвента 2 та 11),

18. DC (резольвента 3 та 6),

19. DD (резольвента 3 та 8),

20. BB (резольвента 3 та 8),

21. DB (резольвента 4 та 6),

22. CB (резольвента 4 та 8),

23. AA (резольвента 5 та 7),

24. DD (резольвента 5 та 7),

25. A (резольвента 5 та 9),

26. CA (резольвента 6 та 10),

27. BA (резольвента 6 та 11),

28. AB (резольвента 7 та 8),

29. D (резольвента 7 та 9),

30. DB (резольвента 7 та 10),

31. DC (резольвента 7 та 11),

32. BA (резольвента 8 та 9),

33. DA (резольвента 8 та 10).

Вилучимо тавтологічні диз’юнкти (13, 14, 19, 20, 23, 24) та ті диз’юнкти, що поглинаються іншими: диз’юнкт 17 поглинає диз’юнкти 2, 5, 9, 10, 11, 25, 26, 27, 32, 33; диз’юнкт 29 – диз’юнкти 3, 4, 7, 12, 16, 18, 21, 30, 31; диз’юнкт 28 – диз’юнкт 1; диз’юнкт 22 – диз’юнкт 15. Отже, залишаються такі диз’юнкти:

6. ВС,

8. BD,

17. A,

22. CB,

28. AB,

29. D.

Побудуємо резольвенти цих диз’юнктів.

34. В (резольвента 6 та 22),

35. В (резольвента 8 та 29),

36. В (резольвента 17 та 28).

Диз’юнкт 34 поглинає диз’юнкти 6, 8, 22, 28, 35 та 36. Отже, залишаються такі диз’юнкти:

17. A,

29. D,

34. В.

Правило резолюції не застосовне до жодної пари цих диз’юнктів.

Таким чином, не існує виводу порожнього диз’юнкту з множини диз’юнктів S, отже, множина диз’юнктів S несуперечна, а це означає, що подана сукупність тверджень сумісна.

Перевіримо суперечність формули F=(AB)(AC)((BC)D)(DA) шляхом побудови приведеної упорядкованої двійкової діаграми рішень.

Виберемо лінійний порядок на множині атомів, що входять у F. Нехай він буде таким: A<B<D<C. Розгалужуємо формулу F по А:

F=AF₁,F₀, де F₁=F[1/A], F₀=F[0/A], тобто:

F₁=(1B)(1C)((BC)D)(D1)=(1B)(0C)((BC)D)1=(1B)1((BC)D)=(1B)((BC)D),

F₀=(0B)(0C)((BC)D)(D0)=1(1C)((BC)D)(D0)=(1C) ((BC)D)(D0).

Отже, F₁=(1B)((BC)D), F₀=(1C)((BC)D)(D0).

Далі розгалужуємо формули F₁ та F₀ по В.

F₁=BF₁₁, F₁₀, де F₁₁=F₁[1/B], F₁₀=F₁[0/B], тобто:

F₁₁=(11)((1C)D)=1(1D)=1D, F₁₀=(10)((0C)D)=0(CD)=0.

F₀=BF₀₁, F₀₀, де F₀₁=F₀[1/B], F₀₀=F₀[0/B], тобто:

F₀₁=(1C)((1C)D)(D0)=(1C)(1D)(D0), F₀₀=(1C)((0C)D)(D0)=(1C)(CD)(D0).

Розгалужуємо формули F₁₁, F₀₁ та F₀₀ по D.

F₁₁=DF₁₁₁, F₁₁₀, де F₁₁₁=F₁₁[1/D], F₁₁₀=F₁₁[0/D], тобто:

F₁₁₁=11=1, F₁₁₀=10=0.

F₀₁=DF₀₁₁, F₀₁₀, де F₀₁₁=F₀₁[1/D], F₀₁₀=F₀₁[0/D], тобто:

F₀₁₁=(1C)(11)(10)=(1C)10=0,

F₀₁₀=(1C)(10)(00)=(1C)01=0.

F₀₀=DF₀₀₁, F₀₀₀, де F₀₀₁=F₀₀[1/D], F₀₀₀=F₀₀[0/D], тобто:

F₀₀₁=(1C)(C1)(10)=(1C)10=0, F₀₀₀=(1C)(C0)(00)=

=(1C)(C0)1=(1C)(C0).

Розгалужуємо формулу F₀₀₀ по С.

F₀₀₀=СF₀₀₀₁, F₀₀₀₀, де F₀₀₀₁=F₀₀₀[1/C], F₀₀₀₀=F₀₀₀[0/C], тобто:

F₀₀₀₁=(11)(10)=10=0, F₀₀₀₀=(11)(10)=10=0.

Усі розгалуження виконано; побудуємо упорядковану ДДР формули F:

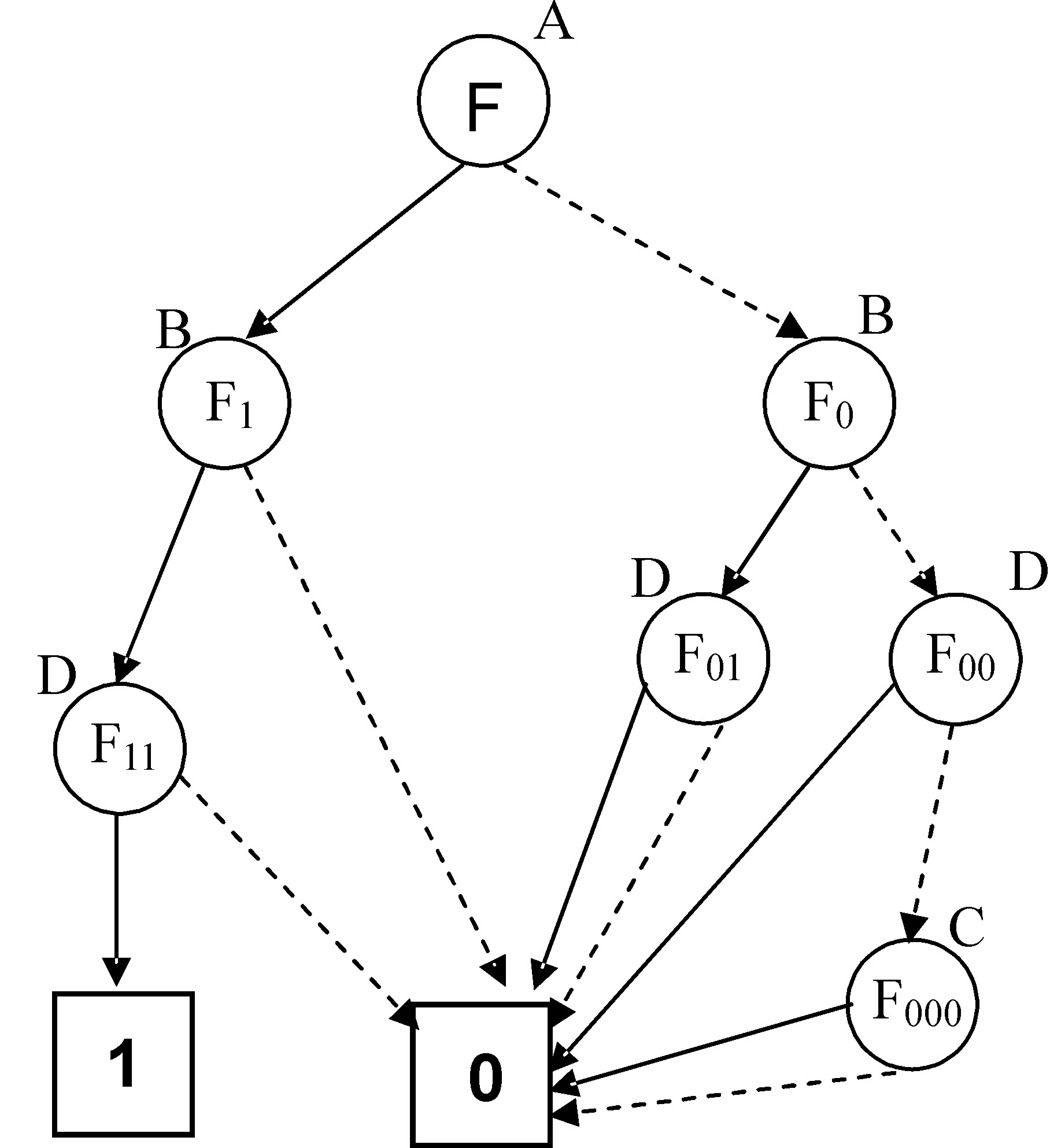
Дана ДДР не є приведеною. Після приведення маємо:

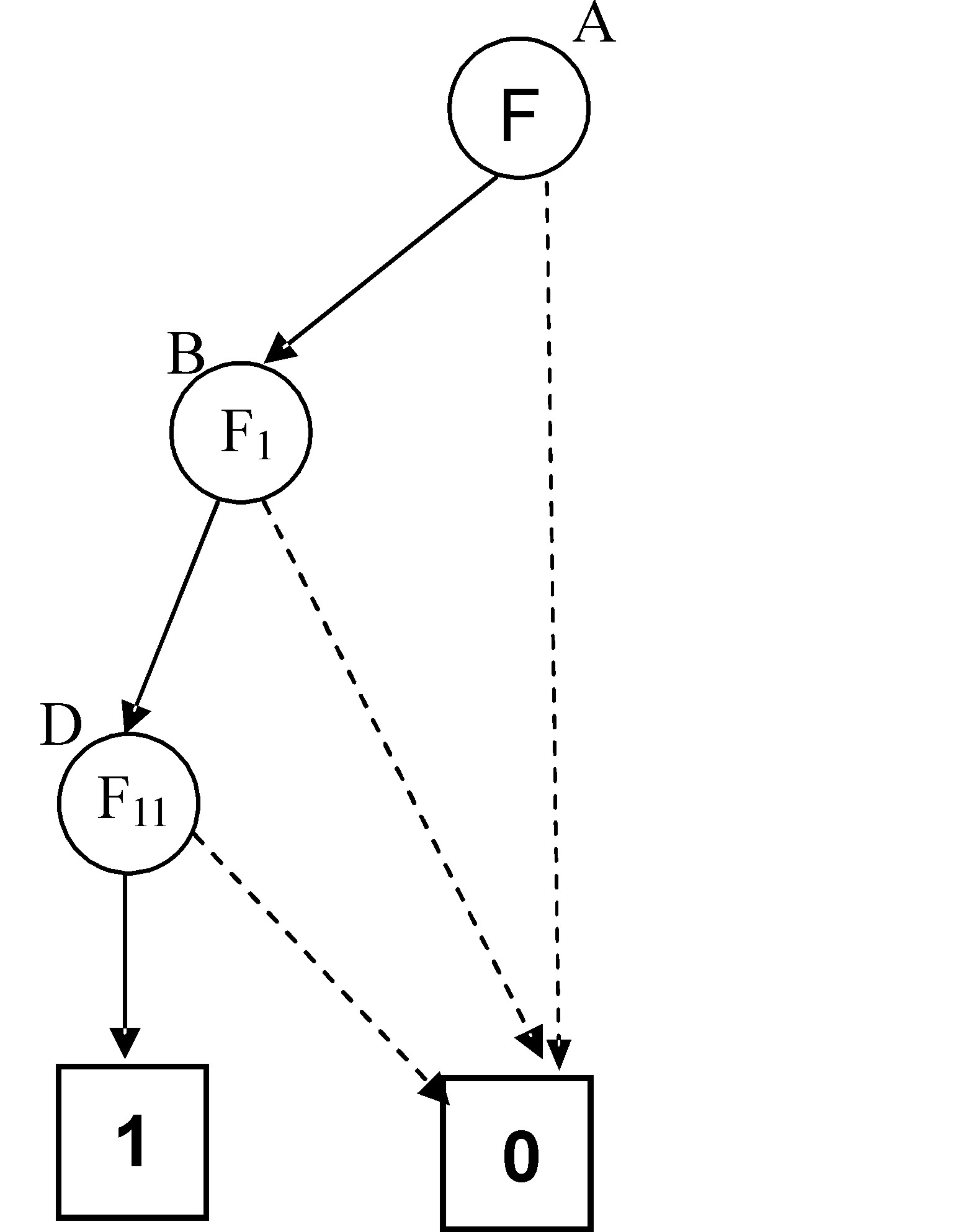
Бачимо, що у приведеній ДДР є кінцева вершина, що має позначку «1», отже, формула F має моделі, тобто не є суперечною. Таким чином, можна зробити висновок, що подана сукупність тверджень є сумісною.

23