Перевірка правильності міркування методом резолюцій

Даний метод дає змогу перевірити суперечність формули, поданої у вигляді множини диз’юнктів.

Розглянемо міркування з першого прикладу й скористаємося побудованими форулами, а також множиною диз’юнктів з попереднього прикладу. Початкова множина диз’юнктів має вигляд: S={AB, ACD, BE, E, C, D}.

Далі для зручності будемо писати диз’юнкти у стовпчик, нумеруючи їх. Також, під час застосування методу резолюцій, деякі диз’юнкти будуть поглинатися іншими диз’юнктами згідно правила: F₁  (F₁  F₂)= F₁. Такі диз’юнкти в подальшому використовуватися не будуть.

Отже, спочатку маємо множину диз’юнктів:

1. AB,

2. ACD,

3. BE,

4. E,

5. C,

6. D.

Оскільки диз’юнкти 3 та 4 містять контрарні літери (Е та Е), до них застосовне правило резолюції. Побудуємо резольвенту диз’юнктів 3 та 4 й занесемо її у множину диз’юнктів під номером 7.

7. B (резольвента диз’юнктів 3 та 4).

Диз’юнкт під номером 3 поглинається диз’юнктом 7, оскільки B  (BE)= B. Отже, диз’юнкт 3 далі можна не розглядати. Множина диз’юнктів буде мати вигляд:

1. AB,

2. ACD,

3. BE (поглинається 7),

4. E,

5. C,

6. D,

7. B (резольвента диз’юнктів 3 та 4).

Далі можна застосувати правило резолюцій до диз’юнктів 2 та 5. Отримаємо такий диз’юнкт:

8. A D (резольвента диз’юнктів 2 та 5).

Оскільки (A D)  (ACD)= A D, то диз’юнкт 2 далі можна не розглядати, й множина диз’юнктів набуває вигляду:

1. AB,

2. ACD (поглинається 8),

3. BE (поглинається 7),

4. E,

5. C,

6. D,

7. B (резольвента диз’юнктів 3 та 4),

8. A D (резольвента диз’юнктів 2 й 5).

Застосувавши правило резолюцій до диз’юнктів 6 та 8, будемо мати:

9. A (резольвента диз’юнктів 6 й 8),

а множина диз’юнктів прийме вигляд:

1. AB,

2. ACD (поглинається 8),

3. BE (поглинається 7),

4. E,

5. C,

6. D,

7. B (резольвента диз’юнктів 3 та 4),

8. A D (резольвента диз’юнктів 2 та 5),

9. A (резольвента диз’юнктів 6 та 8).

Побудуємо резольвенту диз’юнктів 1 та 9:

10. B (резольвента диз’юнктів 1 та 9).

За правилом поглинання В  (AB) = В. Тому перший диз’юнкт далі можна не враховувати, й множина диз’юнктів буде такою:

1. AB (поглинається 10),

2. ACD (поглинається 8),

3. BE (поглинається 7),

4. E,

5. C,

6. D,

7. B (резольвента диз’юнктів 3 та 4),

8. A D (резольвента диз’юнктів 2 та 5),

9. A (резольвента диз’юнктів 6 та 8),

10. B (резольвента диз’юнктів 1 та 9).

Далі, якщо побудувати резольвенту диз’юнктів 7 та 10, отримаємо пустий диз’юнкт .

11.  (резольвента диз’юнктів 7 та 10).

Оскільки існує виведення пустого диз’юнкту з S за допомогою правила резолюції, то початкова множина S є суперечною, а значить, формула (E  C)  D є логічним наслідком формул A  B, (A  C)  D, B  E. Таким чином, задане міркування є логічно правильним.

Перевірка правильності міркування шляхом побудови двійкових діаграм рішень

Розглянемо міркування й задачу про логічне слідування з першого прикладу. Формула (E  C)  D є логічним наслідком формул A  B, (A  C)  D, B  E, якщо формула F = (A  B)  ((A  C)  D)  (B  E)  ((E  C)  D) є суперечністю. Якщо формула F є суперечністю, то упорядкована приведена ДДР, побудована за цією формулою, буде мати вигляд:

Отже, побудуємо упорядковану приведену ДДР формули F й за її виглядом визначимо, чи є F суперечністю.

Спочатку виберемо лінійний порядок на множині атомів, що входять у F. Нехай він буде таким: B<E<A<C<D. Розгалужуємо формулу F по В:

F=В F₁, F₀, де F₁=F[1/В], F₀=F[0/В], тобто

F₁=(A  1)  ((A  C)  D)  (1  E)  ((E  C)  D) = 1  ((A  C)  D)  (1  E)  ((E  C)  D) = ((A  C)  D)  (1  E)  ((E  C)  D);

F₀=(A  0)  ((A  C)  D)  (0  E)  ((E  C)  D) = (A  0)  ((A  C)  D)  1  ((E  C)  D) = (A  0)  ((A  C)  D)  ((E  C)  D).

Далі розгалужуємо формулу F₁ по Е:

F₁=Е F₁₁, F₁₀, де F₁₁=F₁[1/Е], F₁₀=F₁[0/Е], тобто

F₁₁=((A  C)  D)  (1  0)  ((1  C)  D) = ((A  C)  D)  0  (C  D)=0;

F₁₀=((A  C)  D)  (1  1)  ((0  C)  D) = ((A  C)  D)  1  (0  D) = ((A  C)  D)  0 = 0.

Розгалужуємо формулу F₀ по Е:

F₀=Е F₀₁, F₀₀, де F₀₁=F₀[1/Е], F₀₀=F₀[0/Е], тобто

F₀₁ = (A  0)  ((A  C)  D)  ((1  C)  D) = (A  0)  ((A  C)  D)  (C  D);

F₀₀ = (A  0)  ((A  C)  D)  ((0  C)  D) = (A  0)  ((A  C)  D)  (0  D) = (A  0)  ((A  C)  D)  0 = 0.

Розгалужуємо формулу F₀₁ по А:

F₀₁=А F₀₁₁, F₀₁₀, де F₀₁₁=F₀₁[1/А], F₀₁₀=F₀₁[0/А], тобто

F₀₁₁ = (0  0)  ((1  C)  D)  (C  D) = 1  (C  D)  (C  D) = 1  0 = 0;

F₀₁₀ = (1  0)  ((0  C)  D)  (C  D) = 0  (0  D)  (C  D) = 0.

Побудуємо ДДР:

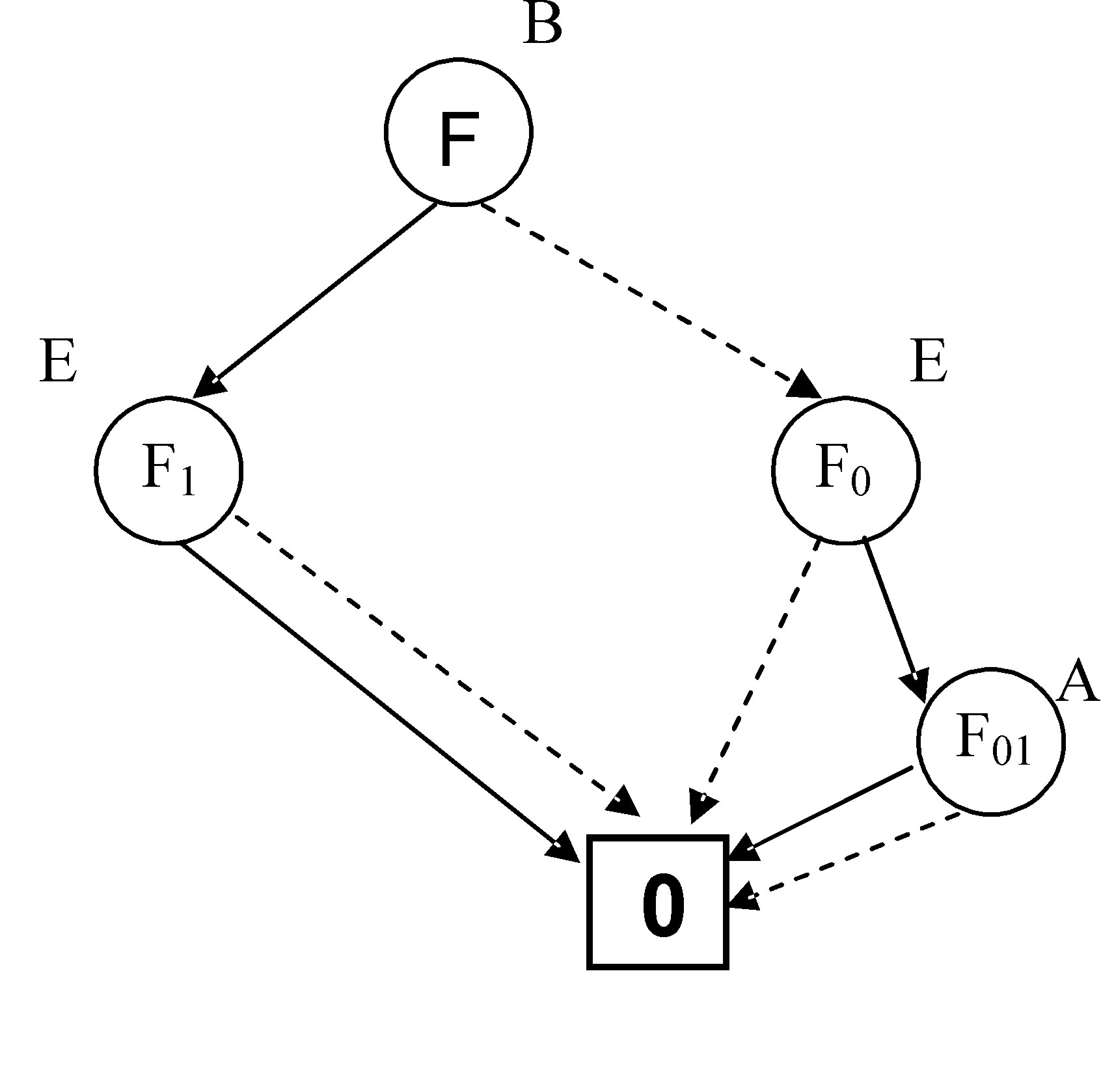
Дана ДДР не є приведеною, оскільки містить вершини виду

Послідовно вилучивши такі вершини, отримаємо:

Отже, формула F є суперечною й формула (E  C)  D є логічним наслідком формул A  B, (A  C)  D, B  E. Таким чином, задане міркування є логічно правильним.