What is the base for obtaining continuity equation?
One of the fundamental principles used in the analysis of uniform flow is known as the Continuity of Flow. This principle is derived from the fact that mass is always conserved in fluid systems regardless of the pipeline complexity or direction of flow. When a fluid is in motion, it must move in such a way that mass is conserved. To see how mass conservation places restrictions on the velocity field, consider the steady flow of fluid through a duct (that is, the inlet and outlet flows do not vary with time). The inflow and outflow are one-dimensional, so that the velocity V and density \rho are constant over the area A (figure 14).
|
|
Figure 14. One-dimensional duct showing control volume. |
Now we apply the principle of mass conservation. Since there is no flow through the side walls of the duct, what mass comes in over A_1 goes out of A_2, (the flow is steady so that there is no mass accumulation). Over a short time interval \Delta t,
Or
Where:
Q = the volumetric flow rate
A = the cross sectional area of flow
V = the mean velocity
This is a statement of the principle of mass conservation for a steady, one-dimensional flow, with one inlet and one outlet. This equation is called the continuity equation for steady one-dimensional flow. For a steady flow through a control volume with many inlets and outlets, the net mass flow must be zero, where inflows are negative and outflows are positive.
69Write integral form of continuity equation and call its members.
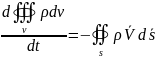
or
where
S is a surface as described above - except this time it has to be a closed surface that encloses a volume V,
denotes
a surface
integral over
a closed surface,
denotes
a volume
integral over V.
is
the total amount of ρ in
the volume V;
is
the total generation (negative in the case of removal) per unit time
by the sources and sinks in the volume V,
Write differential form of continuity equation and call its members.
The differential form for a general continuity equation is (using the same q, ρ and j as above):
Where
∇• is divergence,
t is time,
σ is the generation of q per unit volume per unit time. Terms that generate (σ > 0) or remove (σ < 0) q are referred to as a "sources" and "sinks" respectively.
This general equation may be used to derive any continuity equation, ranging from as simple as the volume continuity equation to as complicated as the Navier–Stokes equations. This equation also generalizes the advection equation. Other equations in physics, such as Gauss's law of the electric field and Gauss's law for gravity, have a similar mathematical form to the continuity equation, but are not usually called by the term "continuity equation", because j in those cases does not represent the flow of a real physical quantity.
In the case that q is a conserved quantity that cannot be created or destroyed (such as energy), this translates to σ = 0, and the continuity equation is:
