58 What is the condition of shock wave detaching from body surface?
-These shocks are curved, and form a small distance in front of the body. Directly in front of the body, they stand at 90 degrees to the oncoming flow, and then curve around the body. Detached shocks allow the same type of analytic calculations as for the attached shock, for the flow near the shock. They are a topic of continuing interest, because the rules governing the shock's distance ahead of the blunt body are complicated, and are a function of the body's shape. Additionally, the shock standoff distance varies drastically with the temperature for a non-ideal gas, causing large differences in the heat transfer to the thermal protection system of the vehicle.
- shock occurs when the maximum deflection angle is exceeded. A detached shock is commonly seen on blunt bodies, but may also be seen on sharp bodies at low Mach numbers.
- Examples: Space return vehicles , bullets, the boundary (Bow shock) of a magnetosphere. The name "bow shock" comes from the example of a bow wave, the detached shock formed at the bow (front) of a ship or boat moving through water, whose slow surface wave speed is easily exceeded
What is coefficient of total pressure lost in normal shock wave . What does it characterize? Write the formula for it calculation.
The shock is a thin boundary across which heat transfer and viscous heating make the flow subsonic. The isentropic relations above are not applicable across a shock wave. The total temperature across a shock (normal to the shock surface) remains constant but the total pressure is lost. The loss depends on the incident Mach number. A higher incident Mach number will transition to a smaller downstream subsonic Mach number.
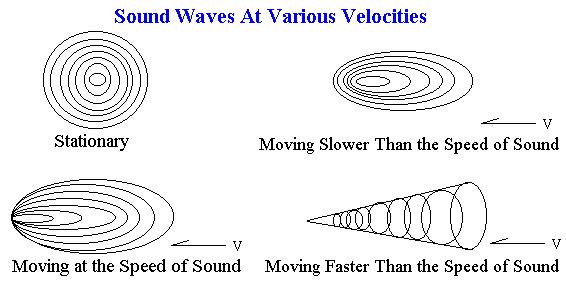
Draw schemes of sound oscillations propagations for follow cases: 1) the source of sound oscillations is fixed; 2) 3) the source of sound oscillations moves with velocity equal speed of sound; 4) the source of sound oscillations moves with velocity grater then speed of sound.
Write the formula presents relation between Mach number and the value of half of cone angle when the velocity of source of sound is supersonic
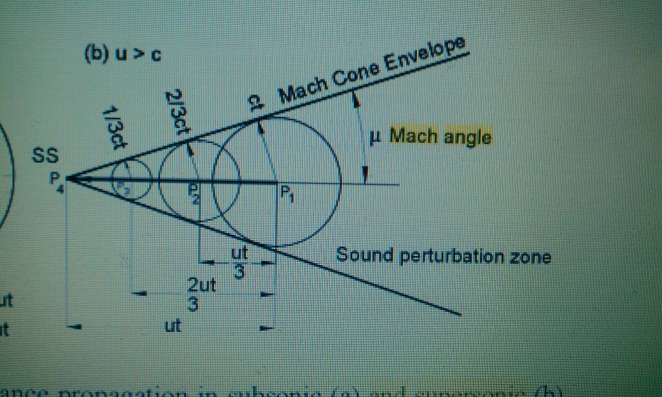
After
the period of time t, the speshial front oh the pressure distribution
has research the radious
.
The sound source moving with supersonic speed form a conical envelop,
The Mach cone, whose angle is calculated
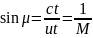. The figure shows that the sound waves reaches the observer within
the Mach cone described by the Mach angle
62 Draw schemes of supersonic flows about convex and concave angles
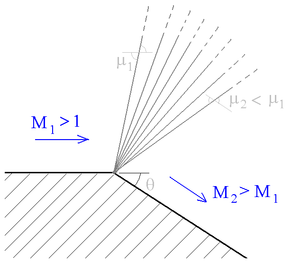
concave angles convex angle
When a supersonic flow encounters a convex corner, it forms an expansion fan, which consists of an infinite number of expansion waves centered at the corner.
63 Give the definition of the shock wave. What is condition for it appearance?
A shock wave is a type of propagating disturbance. A large-amplitude compression wave, as that produced by an explosion or by supersonic motion of a body in a medium.
Like an ordinary wave, it carries energy and can propagate through a medium (solid, liquid, gas or plasma) or in some cases in the absence of a material medium, through a field such as theelectromagnetic field. Shock waves are characterized by an abrupt, nearly discontinuous change in the characteristics of the medium. Across a shock there is always an extremely rapid rise in pressure, temperature and density of the flow. In supersonic flows, expansion is achieved through anexpansion fan. A shock wave travels through most media at a higher speed than an ordinary wave.
Whenever a stream of traffic flowing under certain stream conditions (say, speed = uA , density = kA, and flow = qA) meets another stream flowing under different conditions (say, speed =uB , density = kB, and flow = qB) a shock wave is started. The shock wave is basically the movement of the point that demarcates the two stream conditions. This demarcation point may move forward or backward or stay at the same place with respect to the road. The rate at which this demarcation point moves (the direction of motion of the vehicles is taken as the positive direction) is referred to as the speed of the shock wave.