Give the definition of the stream line, write its differential equation.
Streamline is
a curve that
is instantaneously tangent to
the velocity vector
of the flow. These show the direction a fluid element will travel in
at any point in time.
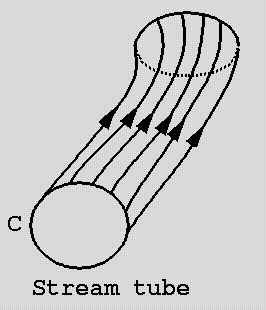
Give the definition of the stream surface, infinitesimal stream tube.
Stream surface is the union of all streamlines seeded densely on a curve. Like a streamline, a stream surface is used to visualize flow.
Infinitesimal stream tube – close surface created by the set of stream lines, whose cross-section is a curve of infinitesimal dimensions.
Essence of Eulers method for investigation of fluid motion .
a)Euler's method focus on the space points, each point in space trying to describe the fluid motion on the change in status over time. The movement of the fluid particle velocity vector can be v=v(x,t) that, where x, t is called Euler variables.
b) The fluid motion is given by completely prescribing the necessary properties as functions of space and time. From this method, we obtain information about the flow in terms of what happens at fixed pointsin space as the fluid flows past those points
Essence of Lagrange method for investigation of fluid motion .
Lagrangian method: is a way of looking at fluid motion where the observer follows an individual fluid parcels as it moves through space and determining how the fluid properties associated with these
particles change as a function of time
Accordance between path line, streamline, Eulers and Lagrange methods for investigation of fluid motion
A fluid flow may be described in two different ways: the Lagrangian approach, and the Eulerian approach. In the Lagrangian approach, one particle is chosen and is followed as it moves through space with time. The line traced out by that one particle is called a particle pathline. A Eulerian approach is used to obtain a clearer idea of the airflow at one particular instant. One can look at a "photograph" of the flow of, for instance, surface ocean currents at a particular fixed time. The entire flow field is easily visualized. The lines comprising this flow field are called streamlines. Thus, a pathline (the Lagrangian point of view) refers to the trace of a single particle in time and space whereas a streamline presents the line of motion of many particles at a fixed time.
Formulate Couchy-Helmholtz theorem.
Motion of liquid element consists of rotational, translational and distortion motions
Write expressions for calculations fluid particle angular velocity projections as functions of derivatives of linear velocity projections, call their members.
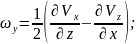
Write expressions for calculations velocity of change of particle angles as functions of derivatives of linear velocity projections, call their members.
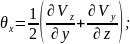
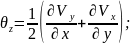
Write fluid particle linear distortion velocity projections calculation formulas, call their members.
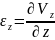
Vx,
Vy,
Vz
– projection center forward speed liquid particles. The values
characterize strain rate tensile (compressive) liquid particles, and
– velocity of change of particles angles.
, etc. – projection velocity of particles around the instantaneous
axis passing through its center. This rotary motuon of a particle
called the vortex, and the projection of the angular velocity of
rotation
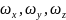components
of the vortex
Write condition of existing irrotational motion of gas (liquid), call their members.
a)Irrotational
means that there is no vorticity (when
the vorticity 
has
the magnitude zero everywhere).
b)The flow
velocity 
of
a fluid is a vector field, and the vorticity
of
the flow can be defined by
If
is
irrotational, with
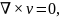then the flow is
said to be an irrotational
flow. The vorticity of
an irrotational flow is zero.
c) exist velocity potential function Q(x,y,z)
Write condition of existing rotational motion of gas (liquid), call their members.
If
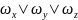is not equal to zero
Give definitions of one dimensional, two dimensional and three dimensional flows.
Term one, two or three dimensional flow refers to the number of space coordinated required to describe a flow. It appears that any physical flow is generally three-dimensional. But these are difficult to calculate and call for as much simplification as possible. This is achieved by ignoring changes to flow in any of the directions, thus reducing the complexity.
Flow is one dimensional if the flow parameters (such as velocity, pressure, depth etc.) at a given instant in time only vary in the direction of flow and not across the cross-section. The flow may be unsteady, in this case the parameter vary in time but still not across the cross-section. An example of one-dimensional flow is the flow in a pipe.
Flow is two-dimensional if it can be assumed that the flow parameters vary in the direction of flow and in one direction at right angles to this direction. Streamlines in two-dimensional flow are curved lines on a plane and are the same on all parallel planes.
In three-dimensional flow the hydrodynamic parameters are functions of three space coordinates and time. Fluid flow is three-dimensional in nature
Give definitions of the plane flow.
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of a gradient always being equal to zero.
U(x,y) – velocity potential function
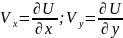
Give the definition of the vortex line, write its differential equation.
Vortex line – line in which point tangent is parallel to angular velocity.
– differential
equation of vortex line
Give the definition of the vortex surface, vortex tube, vortex infinitesimal tube
A vortex tube is the surface in the fluid formed by all vortex-lines passing through a given (reducible) closed curve in the fluid. Vortex surface is the union of all vortex lines seeded densely on a curve. An infinitesimal vortex tube ia a vortex tube whose cross-section is of infinitesimal dimensions.
Give the definition of the vortex filament. Write vortex filament strength calculation formula, call its members.
vortex filament is a vortex tube with infinite small cross section area. In this tube flow has vorticity, . (In the limit as a diameter of the tube is made small, but circulation, Г, is held fixed, this region of orticity is called a vortex filament).
– strength
of vortex filament
Give the definition of velocity circulation . Write the formula for velocity circulation calculation, call its members.
Velocity circulation is the line integral around a closed curve of the velocity field.
The circulation around a closed curve L is the line integral
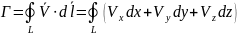
V is the fluid velocity on a small element of a defined curve, and dl is a vector representing the differential length of that small element, the contribution of that differential length to circulation is dΓ
Give the definition of the vortex. Write the formula for vortex strength calculation, call its members.
A vortex is a region within a fluid where the flow is mostly a spinning motion about an imaginary axis, straight or curved. That motion pattern is called a vortical flow
Formulate Stokes theorem.
a)Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Stokes' theorem says that the integral of a differential form ω over the boundary of some orientable manifold Ω is equal to the integral of its exterior derivative dω over the whole of Ω, i.e.
b)S- an oriented, piecewise-smooth surface
C - a simple, closed, piecewise-smooth curve that bounds S
F - a vector field whose components have continuous derivatives in an open region of R3 containing S
Stokes'
Theorem:
Formulate Helmholtz theorem.
Helmholtz's theorems describe the three-dimensional motion of fluid in the vicinity of vortex filaments. These theorems apply to inviscid flows and flows where the influence of viscous forces are small and can be ignored.
Helmholtz’s three theorems are as follows: Helmholtz’s first theorem: The strength of a vortex filament is constant along its length.
Helmholtz’s second theorem: A vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path.
Helmholtz’s third theorem: In the absence of rotational external forces, a fluid that is initially irrotational remains irrotational.
Helmholtz’s theorems apply to inviscid flows. In observations of vortices in real fluids the strength of the vortices always decays gradually due to the dissipative effect of viscous forces.
Alternative expressions of the three theorems are as follows: 1. The strength of a vortex tube does not vary with time. 2. Fluid elements lying on a vortex line at some instant continue to lie on that vortex line. More simply, vortex lines move with the fluid. Also vortex lines and tubes must appear as a closed loop, extend to infinity or start/end at solid boundaries. 3. Fluid elements initially free of vorticity remain free of vorticity.
Draw (or describe verbally) possible shapes of vortex.
1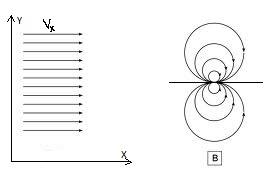
)Uniform
flow along x-axes:
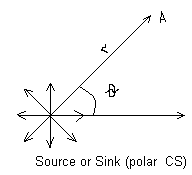
2) Sourcs or Sink (polar CS)
-
strength of the source
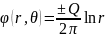
3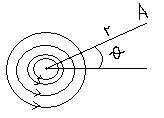
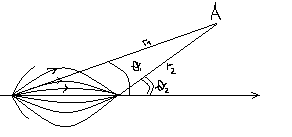)Point
vortex flow
4) Source/Sink
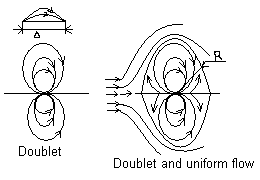
5) Doublet
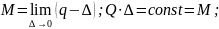
6)Doublet and uniform flow
W
rite
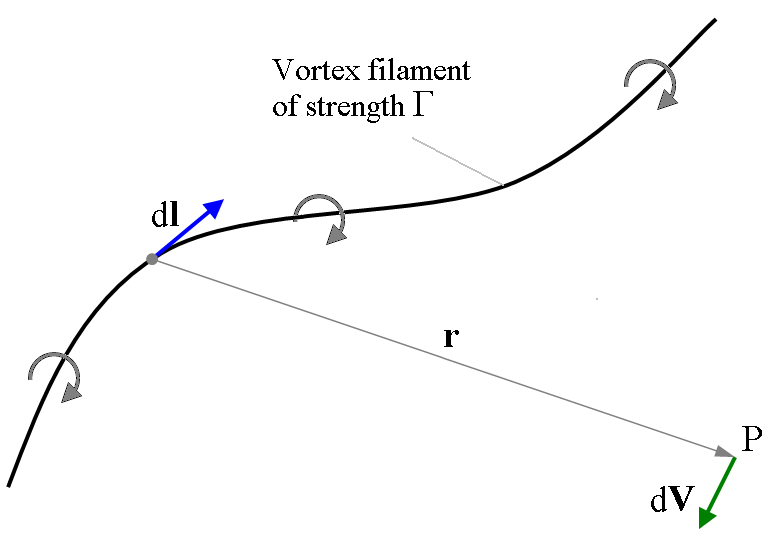
Biot-Savart law for calculation velocity induced by infinitesimal
segment of vortex (call members of these expression).
The
figure shows the velocity (
)
induced at a point P by an element of
vortex
filament
(
)
of strength 
.
r – dist from point P to the element of vortex
Write formula for calculation velocity induced by infinite straight line vortex (call members of these expression).
-
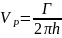
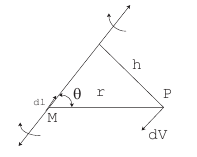
circulation of a vortex filament with; r – dist from point P to the
element of vortex;
-
velocity at point P induced by
infinite straight line vortex;
-
angle between r and dl;
Write formula for calculation velocity induced by half of infinite straight line vortex (call members of these expression).
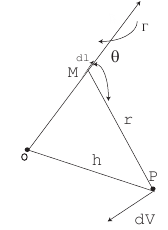
- circulation of a vortex filament with; r – dist from point P to the element of vortex; - velocity at point P induced by half of infinite straight line vortex; - angle between r and dl;
As a base for Euler’s equation obtaining is used (point right answer number): 1) Dalamberts principle; 2) I Newton law; 3) II Newton law; 3) III Newton law; 4) I thermodynamic principle; 5) II thermodynamic principle.
Anser#2 - first Newton law
Euler’s equation
does not take in to account (point right answer number): 1) Gas
viscosity; 2) Gas compressibility; 3) Gas barotropic; 4) Unsteady
flow; 5) Turbulent flow.
Answer #4 – unsteady flow
For Euler’s equation install correspondence between letters from it and physical values names:
- is , ρ
–
is
, p
- is ,
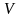- is , t
- is , grad
–
is (density, time, pressure, velocity, body force, mathematic
operator
)
-is
the fluid mass
density;
p – pressure; V –velocity, t- time, grad – mathematical
operator
For Euler’s equation point out dimensions of values, which are marked by letters: , ρ, p, V, t.
F
=N,
=
,
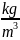p=Pa, V=
;
t=s;
Follow form of Euler’s equation
may be integrated in closed form in 5 cases from given 6: 1) along
streamline; 2) along vortex line; 3) for irrotational flow; 4) along
screw line; 5) isobar line; 6) absence of gas motion. Point these
cases.
Ніде нема, велика вірогідність що (1,3,4,5,6)
Write Zhukovsky formula. Call its members.
The
theorem refers to two-dimensional flow around a cylinder (or a
cylinder of infinite span)
and determines the lift generated by one unit of span. When the
circulation Г is
known, the lift L per
unit span (or L’)
of the cylinder can be calculated using the following equation:
where 
and 
are
the fluid density and the fluid velocity far upstream of the
cylinder, and 
is
the (anticlockwise positive) circulation defined as the line
integral,
around
a closed contour 
enclosing
the cylinder or airfoil and followed in the positive (anticlockwise)
direction. The
integrand 
is
the component of the local fluid velocity in the direction tangent to
the curve
and 
is
an infinitesimal length on the curve,
Value under differential sign in follow form of Euler’s equation
is
constant in 5 cases from given 6: 1) along streamline; 2) along
vortex line; 3) for irrotational flow; 4) along screw line; 5)
isobar line; 6) absence of gas motion. Point these cases.
Is const in 5 cases (1-stream line, 2-vortex line, 4 – screw, 3 – irrotational flow, 5 – isobar)
For Euler’s equation in follow form install correspondence between letters from it and physical values names:
U
– is potential force function, Π
–
is
notation for expression
V
– is velocity vector magnitude, ωx,
ωy,
ωz
- are angular velocity projections, Vx,
Vy,
Vz
-
are linear velocity projections
For Euler’s equation in follow form what value (U,Π,
,
)
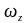corresponds expression
Answer:
Π
corresponds for
Euler’s equation is written in form corresponds the assumption that flow is: 1) unsteady; 2) incompressible; 3) steady; 4) potential; 5) barotropic. Point right assumption.
Answer:
4)potential
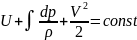
Bernoulli integral
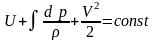is obtained from Euler’s equation
is
correct for in 5 cases from given 6:
1) along streamline;
2) along vortex line;
3) for irrotational flow;
4) along screw line;
6) absence of gas motion.
Bernoulli integral is obtained from Euler’s equation using assumption that potential force function U corresponds to conditions of: 2) arbitrary mass force field; (perecprocit)
37 There are four Bernoulli equation notations:
1)
;
incompressible gas case
2)
;
incompressible gas case
3)
;
compressible gas case
4)
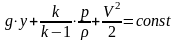.compressible
gas case
38
Bernoulli integral
is converted to Bernoulli equation for ; 3) inviscid flow; 4)
adiabatic compressible gas
Bernoulli equation is written in follow notations ????
does
not take into account: 1) gas compressibility; 2) actions of
potential mass forces; 3) actions of inertial mass forces; 4) gas
barotropic. Point right case (cases).
40
For follow Bernoulli equation notations
install
correspondence between letters from them and physical values names:
i
- enthalpy , p
–
pressure
, V
- velocity ,ρ-
density , T
-
temperature , R
– gas constant , a
– speed of sound