1. Give the definition of the stream line, write its differential equation.

Streamline is a curve that is instantaneously tangent to the velocity vector of the flow. These show the direction a fluid element will travel in at any point in time.

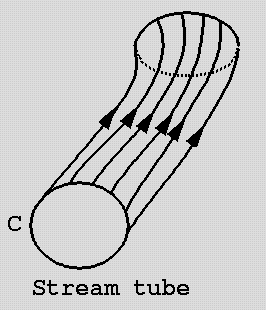
2. Give the definition of the stream surface, infinitesimal stream tube.

Stream surface is the union of all streamlines seeded densely on a curve. Like a streamline, a stream surface is used to visualize flow.

Infinitesimal stream tube – close surface created by the set of stream lines, whose cross-section is a curve of infinitesimal dimensions.

3. Essence of Eulers method for investigation of fluid motion .

a)Euler's method focus on the space points, each point in space trying to describe the fluid motion on the change in status over time. The movement of the fluid particle velocity vector can be v=v(x,t) that, where x, t is called Euler variables.

b) The fluid motion is given by completely prescribing the necessary properties as functions of space and time. From this method, we obtain information about the flow in terms of what happens at fixed pointsin space as the fluid flows past those points

4. Essence of Lagrange method for investigation of fluid motion .

Lagrangian method: is a way of looking at fluid motion where the observer follows an individual fluid parcels as it moves through space and determining how the fluid properties associated with these

particles change as a function of time

5. Accordance between path line, streamline, Eulers and Lagrange methods for investigation of fluid motion

A fluid flow may be described in two different ways: the Lagrangian approach, and the Eulerian approach. In the Lagrangian approach, one particle is chosen and is followed as it moves through space with time. The line traced out by that one particle is called a particle pathline. A Eulerian approach is used to obtain a clearer idea of the airflow at one particular instant. One can look at a "photograph" of the flow of, for instance, surface ocean currents at a particular fixed time. The entire flow field is easily visualized. The lines comprising this flow field are called streamlines. Thus, a pathline (the Lagrangian point of view) refers to the trace of a single particle in time and space whereas a streamline presents the line of motion of many particles at a fixed time.

6. Formulate Couchy-Helmholtz theorem.

7. Write expressions for calculations fluid particle angular velocity projections as functions of derivatives of linear velocity projections, call their members.

8. Write expressions for calculations velocity of change of particle angles as functions of derivatives of linear velocity projections, call their members.

9. Write fluid particle linear distortion velocity projections calculation formulas, call their members.

10. Write condition of existing irrotational motion of gas (liquid), call their members.

11. Write condition of existing rotational motion of gas (liquid), call their members.

12. Give definitions of one dimensional, two dimensional and three dimensional flows.

13. Give definitions of the plane flow.

14. Give the definition of the vortex line, write its differential equation.

15. Give the definition of the vortex surface, vortex tube, vortex infinitesimal tube

16. Give the definition of the vortex filament. Write vortex filament strength calculation formula, call its members.

17. Give the definition of velocity circulation . Write the formula for velocity circulation calculation, call its members.

18. Give the definition of the vortex. Write the formula for vortex strength calculation, call its members.

19. Formulate Stokes theorem.

20. Formulate Helmholtz theorem.

21. Draw (or describe verbally) possible shapes of vortex.

22. Write Biot-Savart law for calculation velocity induced by infinitesimal segment of vortex (call members of these expression).

23. Write formula for calculation velocity induced by infinite straight line vortex (call members of these expression).

24. Write formula for calculation velocity induced by half of infinite straight line vortex (call members of these expression).

25. As a base for Euler’s equation obtaining is used (point right answer number): 1) Dalamberts principle; 2) I Newton law; 3) II Newton law; 3) III Newton law; 4) I thermodynamic principle; 5) II thermodynamic principle.

26. Euler’s equation does not take in to account (point right answer number): 1) Gas viscosity; 2) Gas compressibility; 3) Gas barotropic; 4) Unsteady flow; 5) Turbulent flow.

27. For Euler’s equation install correspondence between letters from it and physical values names: - is , ρ – is , p - is , 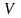- is , t - is , grad – is (density, time, pressure, velocity, body force, mathematic operator )

28. For Euler’s equation point out dimensions of values, which are marked by letters: , ρ, p, V, t.

29. Follow form of Euler’s equation may be integrated in closed form in 5 cases from given 6: 1) along streamline; 2) along vortex line; 3) for irrotational flow; 4) along screw line; 5) isobar line; 6) absence of gas motion. Point these cases.

30. Write Zhukovsky formula. Call its members.

31. Value under differential sign in follow form of Euler’s equation is constant in 5 cases from given 6: 1) along streamline; 2) along vortex line; 3) for irrotational flow; 4) along screw line; 5) isobar line; 6) absence of gas motion. Point these cases.

32. For Euler’s equation in follow form install correspondence between letters from it and physical values names: U - is , Π – is , V - is , ω_x, ω_y, ω_z - are , V_x, V_y, V_z - are (linear velocity projections, potential force function, velocity vector magnitude, angular velocity projections, notation for expression )

33. For Euler’s equation in follow form what value (U,Π, , ) corresponds expression

34. Euler’s equation is written in form corresponds the assumption that flow is: 1) unsteady; 2) incompressible; 3) steady; 4) potential; 5) barotropic. Point right assumption.

35. Bernoulli integral 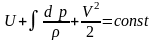is obtained from Euler’s equation is correct for in 5 cases from given 6: 1) along streamline; 2) along vortex line; 3) for irrotational flow; 4) along screw line; 5) isobar line; 6) absence of gas motion. Point these cases.

36. Bernoulli integral is obtained from Euler’s equation using assumption that potential force function U corresponds to conditions of: 1) earth gravity field; 2) arbitrary mass force field; 3) arbitrary inertial force field; 4) steady rotation inertial force field. Point correct assamption.

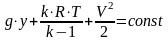37. There are four Bernoulli equation notations: 1) ; 2) ; 3) ; 4) . Part of them corresponds compressible gas case, another – incompressible. Write notation numbers for each case.

38. Bernoulli integral is converted to Bernoulli equation for 2 cases from 5 given: 1) incompressible gas; 2) potential flow; 3) inviscid flow; 4) adiabatic compressible gas; 5) laminar flow. Point right cases.

39. Bernoulli equation is written in follow notations does not take into account: 1) gas compressibility; 2) actions of potential mass forces; 3) actions of inertial mass forces; 4) gas barotropic. Point right case (cases).

40. For follow Bernoulli equation notations install correspondence between letters from them and physical values names: k - is , p – is , V - is ,ρ- is , T - is , R – is , a – is , i – is (velocity, density, temperature, pressure, gas constant, speed of sound, enthalpy)

41. What principle is a base for obtaining differential equation of inviscid gas motion? Name and formulate it.

42. Which forces act in flow and are taken into account during obtaining differential equation of inviscid gas motion?

43. Write vector form of Euler’s equation for inviscid gas motion and call equation members.

44. Call flow condition where Euler’s equation has closed form solution.

45. Write Euler’s equation solution, which is named Bernoulli’s integral. Call its members.