Formulate Helmholtz theorem.
Helmholtz's theorems describe the three-dimensional motion of fluid in the vicinity of vortex filaments. These theorems apply to inviscid flows and flows where the influence of viscous forces are small and can be ignored.
Helmholtz’s three theorems are as follows: Helmholtz’s first theorem: The strength of a vortex filament is constant along its length.
Helmholtz’s second theorem: A vortex filament cannot end in a fluid; it must extend to the boundaries of the fluid or form a closed path.
Helmholtz’s third theorem: In the absence of rotational external forces, a fluid that is initially irrotational remains irrotational.
Helmholtz’s theorems apply to inviscid flows. In observations of vortices in real fluids the strength of the vortices always decays gradually due to the dissipative effect of viscous forces.
Alternative expressions of the three theorems are as follows: 1. The strength of a vortex tube does not vary with time. 2. Fluid elements lying on a vortex line at some instant continue to lie on that vortex line. More simply, vortex lines move with the fluid. Also vortex lines and tubes must appear as a closed loop, extend to infinity or start/end at solid boundaries. 3. Fluid elements initially free of vorticity remain free of vorticity.
Draw (or describe verbally) possible shapes of vortex.
1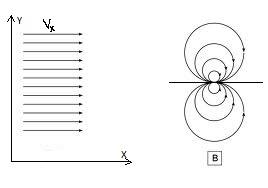
)Uniform
flow along x-axes:
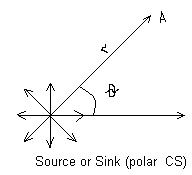
2) Sourcs or Sink (polar CS)
-
strength of the source
3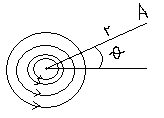
)Point
vortex flow
4) Source/Sink
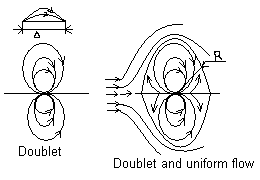
5) Doublet
6)Doublet and uniform flow
W
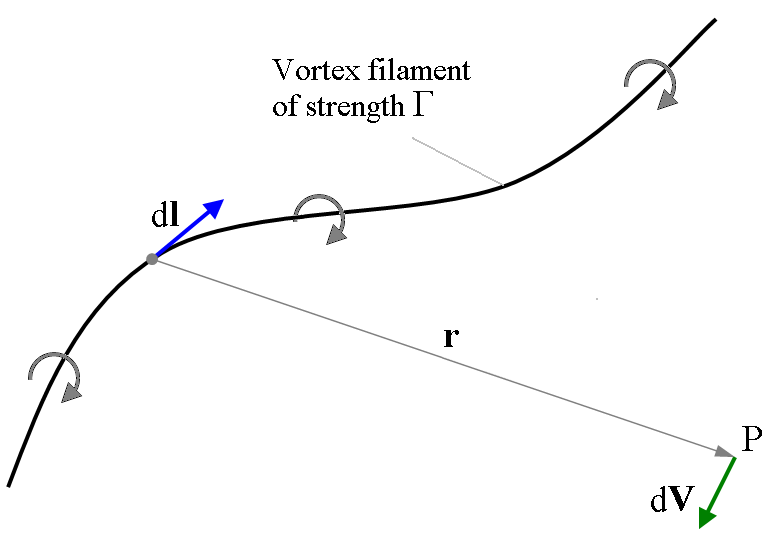rite
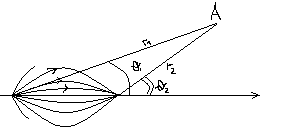
Biot-Savart law for calculation velocity induced by infinitesimal
segment of vortex (call members of these expression).
The
figure shows the velocity (
)
induced at a point P by an element of
vortex
filament
(
)
of strength 
.
r – dist from point P to the element of vortex
Write formula for calculation velocity induced by infinite straight line vortex (call members of these expression).
-
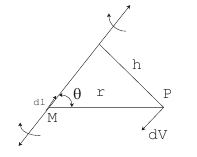
circulation of a vortex filament with; r – dist from point P to the
element of vortex;
-
velocity at point P induced by
infinite straight line vortex;
-
angle between r and dl;
Write formula for calculation velocity induced by half of infinite straight line vortex (call members of these expression).
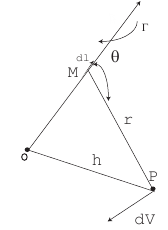
- circulation of a vortex filament with; r – dist from point P to the element of vortex; - velocity at point P induced by half of infinite straight line vortex; - angle between r and dl;
As a base for Euler’s equation obtaining is used (point right answer number): 1) Dalamberts principle; 2) I Newton law; 3) II Newton law; 3) III Newton law; 4) I thermodynamic principle; 5) II thermodynamic principle.
Anser#2 - first Newton law
Euler’s equation
does not take in to account (point right answer number): 1) Gas
viscosity; 2) Gas compressibility; 3) Gas barotropic; 4) Unsteady
flow; 5) Turbulent flow.
Answer #4 – unsteady flow
For Euler’s equation install correspondence between letters from it and physical values names:
- is , ρ
–
is
, p
- is ,
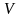- is , t
- is , grad
–
is (density, time, pressure, velocity, body force, mathematic
operator
)
-is
the fluid mass
density;
p – pressure; V –velocity, t- time, grad – mathematical
operator
For Euler’s equation point out dimensions of values, which are marked by letters: , ρ, p, V, t.
F
=N,
=
,
p=Pa, V=
;
t=s;
Follow form of Euler’s equation
may be integrated in closed form in 5 cases from given 6: 1) along
streamline; 2) along vortex line; 3) for irrotational flow; 4) along
screw line; 5) isobar line; 6) absence of gas motion. Point these
cases.
Ніде нема, велика вірогідність що (1,3,4,5,6)
Write Zhukovsky formula. Call its members.
The
theorem refers to two-dimensional flow around a cylinder (or a
cylinder of infinite span)
and determines the lift generated by one unit of span. When the
circulation Г is
known, the lift L per
unit span (or L’)
of the cylinder can be calculated using the following equation:
where 
and 
are
the fluid density and the fluid velocity far upstream of the
cylinder, and 
is
the (anticlockwise positive) circulation defined as the line
integral,
around
a closed contour 
enclosing
the cylinder or airfoil and followed in the positive (anticlockwise)
direction. The
integrand 
is
the component of the local fluid velocity in the direction tangent to
the curve
and 
is
an infinitesimal length on the curve,
Value under differential sign in follow form of Euler’s equation
is
constant in 5 cases from given 6: 1) along streamline; 2) along
vortex line; 3) for irrotational flow; 4) along screw line; 5)
isobar line; 6) absence of gas motion. Point these cases.
Is const in 5 cases (1-stream line, 2-vortex line, 4 – screw, 3 – irrotational flow, 5 – isobar)
For Euler’s equation in follow form install correspondence between letters from it and physical values names:
U
– is potential force function, Π
–
is
notation for expression
V
– is velocity vector magnitude, ωx,
ωy,
ωz
- are angular velocity projections, Vx,
Vy,
Vz
-
are linear velocity projections
For Euler’s equation in follow form what value (U,Π,
,
)
corresponds expression
Answer:
Π
corresponds
for
Euler’s equation is written in form corresponds the assumption that flow is: 1) unsteady; 2) incompressible; 3) steady; 4) potential; 5) barotropic. Point right assumption.
Answer:
4)potential
