1. Give the definition of the stream line, write its differential equation.

Streamline is a curve that is instantaneously tangent to the velocity vector of the flow. These show the direction a fluid element will travel in at any point in time.

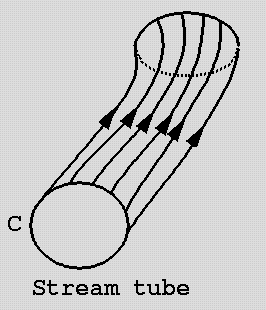
2. Give the definition of the stream surface, infinitesimal stream tube.

Stream surface is the union of all streamlines seeded densely on a curve. Like a streamline, a stream surface is used to visualize flow.

Infinitesimal stream tube – close surface created by the set of stream lines, whose cross-section is a curve of infinitesimal dimensions.

3. Essence of Eulers method for investigation of fluid motion .

a)Euler's method focus on the space points, each point in space trying to describe the fluid motion on the change in status over time. The movement of the fluid particle velocity vector can be v=v(x,t) that, where x, t is called Euler variables.

b) The fluid motion is given by completely prescribing the necessary properties as functions of space and time. From this method, we obtain information about the flow in terms of what happens at fixed pointsin space as the fluid flows past those points

4. Essence of Lagrange method for investigation of fluid motion .

Lagrangian method: is a way of looking at fluid motion where the observer follows an individual fluid parcels as it moves through space and determining how the fluid properties associated with these

particles change as a function of time

5. Accordance between path line, streamline, Eulers and Lagrange methods for investigation of fluid motion

A fluid flow may be described in two different ways: the Lagrangian approach, and the Eulerian approach. In the Lagrangian approach, one particle is chosen and is followed as it moves through space with time. The line traced out by that one particle is called a particle pathline. A Eulerian approach is used to obtain a clearer idea of the airflow at one particular instant. One can look at a "photograph" of the flow of, for instance, surface ocean currents at a particular fixed time. The entire flow field is easily visualized. The lines comprising this flow field are called streamlines. Thus, a pathline (the Lagrangian point of view) refers to the trace of a single particle in time and space whereas a streamline presents the line of motion of many particles at a fixed time.

6. Formulate Couchy-Helmholtz theorem.

Motion of liquid element consists of rotational, translational and distortion motions

7. Write expressions for calculations fluid particle angular velocity projections as functions of derivatives of linear velocity projections, call their members.

8. Write expressions for calculations velocity of change of particle angles as functions of derivatives of linear velocity projections, call their members.

9. Write fluid particle linear distortion velocity projections calculation formulas, call their members.

V_x, V_y, V_z – projection center forward speed liquid particles. The values characterize strain rate tensile (compressive) liquid particles, and – velocity of change of particles angles. , etc. – projection velocity of particles around the instantaneous axis passing through its center. This rotary motuon of a particle called the vortex, and the projection of the angular velocity of rotation components of the vortex