- •Тема: требования к математической модели
- •Общая схема построения уравнений движения
- •Требования к математической модели
- •Задание 1 Движение тела, брошенного под углом к горизонту.
- •3. Оценка учета изменения с высотой величины ускорения силы тяжести Земли.
- •Требования к выполнению задания
- •Примерная структура оформления результатов
- •Возможная расчетная схема вариантов
ЛАБОРАТОРНАЯ РАБОТА № 2
по курсу «Моделирование сложных систем»
Тема: требования к математической модели
Цель работы. Освоение методологии построения адекватных математических моделей объекта и исследований с их помощью параметров его движения.
Общая схема построения уравнений движения
Законы Ньютона.
Рассматривается система, модель которой может быть представлена как материальная точка.
Материальная точка - тело, размеры и форма которого несущественны в рассматриваемой задаче. Движение материальной точки полностью задано, если указан однозначный закон изменения во времени ее пространственных координат. Траектория – линия, описываемая движущейся точкой в пространстве.
Система материальных точек (механическая система) совокупность материальных точек, которая в общем случае взаимодействует как друг с другом, так и с другими телами, не включенными в систему.
Инерционные свойства механической системы выражаются первым и вторым законами Ньютона.
Под действием внешней силы точка приобретает конечное по величине ускорение, в отсутствие внешних воздействий – сохраняет состояние покоя или равномерного прямолинейного движения.
Количество движения материальной точки – вектор Кi, равный произведению массы точки mi на ее скорость vi: Кi = mi vi:
1-ый закон - если на материальную точку не действуют другие тела, то она находится в состоянии покоя или равномерного прямолинейного движения.
Этот закон называют законом инерции движения материальной точки, свободной от внешних воздействий – движением по инерции.
2-й закон - произведение массы тела на ускорение равно сумме всех действующих на тело сил ma = F.
Закон устанавливает связь между действующей силой и вызванным ею изменением состояния (ускорением): ускорение материальной точки прямо пропорционально действующей на нее силе F ~ a.
Отношение силы к приобретенному ускорению постоянно для данного тела. Это отношение называется массой.
Масса = Сила / Ускорение
Здесь масса характеризует инерционные свойства материальной точки и называется инертной массой материальной точки.
Или: первая производная по времени от импульса (количества движения) материальной точки (системы точек) равна главному вектору F всех внешних сил, приложенных к точке (элементарное изменение количества движения материальной точки равно элементарному импульсу действующей на нее силы):
![]() = Fi
или
= Fi
или
![]() (mivi)
= Fi
,
d (mivi)
= Fi
dt
(mivi)
= Fi
,
d (mivi)
= Fi
dt
так как mi = const, то аi = dvi / dt = Fi / mi, или ma = F.
Итак, второй закон Ньютона для материальной частицы m¨x = F.
Здесь m – масса частицы, x(t) = (x1(t), x2(t), x3(t)) – ее положение в момент времени t.
Частица движется в пространстве R3, x1(t), x2(t), x3(t) – ее координаты, F - действующая на частицу сила, может задаваться как функция времени F = F (t). Обычно сила задается как вектор-функция аргументов x R3, x˙ R3 и времени t. Тогда уравнение второго закона есть векторное дифференциальное уравнение второго порядка mx¨ = F(x, x˙, t).
Для того, чтобы описать движение материальной точки при помощи этого уравнения, недостаточно задать ее начальное положение, задание начальных условий должно включать и задание начальной скорости:
x(0) = x0, x˙ (0) = v0.
Здесь x0 – начальное положение точки x0(t) = (x01, x02, x03) R3, v0(t) = (v01, v02, v03) R3 – ее начальная скорость.
Таким образом, фазовое пространство данной системы есть R3 х R3, а состояние системы – есть пара (x, v), где x - положение материальной точки, v - ее скорость.
Согласно первому и второму законам Ньютона все изменения состояния движения вызываются силами – силы являются причинами любого изменения.
Ускорение возникает в направлении действия силы. Силы инерции направлены в противоположную сторону. Возникают только в системе отсчета, движущейся с ускорением – это кажущиеся силы.
3-ий закон - две материальные точки действуют друг на друга с силами, равными по величине и направленными в противоположные стороны вдоль прямой, соединяющей эти точки.
Fij = - Fji.
Fij - сила, действующая на i–ю точку со стороны j–ой точки.
Тяготение между телами осуществляется через гравитационное поле (поле тяготения.
Здесь масса материальной точки характеризует гравитационные свойства этой точки и называется гравитационной массой (массой тяжести).
Векторная характеристика гравитационного поля – его напряженность g, которая равна отношению силы тяготения, действующей на материальную точку, к его массе: g = Р/m.
Для всех тел отношение их инертных и гравитационных масс постоянно. Инертные и гравитационные массы равны и связаны с силой тяжести тела соотношением P = mg.
Вес тела – сила, с которой тело вследствие тяготения к центру притяжения действует на опору (или подвес), удерживающую тело от свободного падения. Невесомость – состояние системы, при котором на систему не действуют никакие внешние силы, кроме силы гравитационного поля. Свободным падением называется движение тела под действием единственной силы, равной его весу.
Вес тела Р равен векторной разности силы F тяготения тела к Земле и центростремительной силы Fц, обуславливающей участие тела во вращении Земли:
Р = F - Fц. Центростремительная сила Fц зависит от массы тела m, угловой скорости суточного вращения Земли ω, радиуса Земли R, географической широты места наблюдения φ:Fц = m ω2Rcos φ.
На географических полюсах (φ = 900) Fц = 0 и вес тела равен силе притяжения его к Земле. Вследствие того, что центростремительная сила зависит от широты, вес тела максимален на полюсах и минимален на экваторе, различие не превышает 0,55%.
Ускорение свободного падения одинаково для всех тел и, также как и вес, зависит от географической широты и высоты над уровнем моря.
Стандартное (нормальное) значение ускорения свободного падения на уровне моря составляет g0 = 9,81 м.сек2. Для определения ускорения при удалении от поверхности Земли на высоту h используется формула g = g0[R0/(R0 + h)]2, R0 = 6370 км - радиус Земли.
Закон всемирного тяготения: между любыми двумя материальными точками действуют силы взаимного притяжения
![]() ,
,
где f - гравитационная постоянная (сила взаимного притяжения между двумя точками одинаковой массы на расстоянии единицы длины).
Закон Архимеда – на погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости, вытесненной телом:
По закону Архимеда выталкивающая сила равна F = gVρ0.
Сила приложена в центре тяжести объема погруженной части тела.
Уравнения движения
Согласно законам Ньютона все изменения состояния движения вызываются силами.
Принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них сообщает точке ускорение, определяемое 2-м законом Ньютона так, как если бы других сил не было, результирующее ускорение определяется действием результирующей силы.
Если какое либо предположение о движении не подчиняется этим законам, его следует из рассмотрения исключить.
Тело может находиться в равновесии, если сумма проекций приложенных к нему сил на любое направление равна нулю.
Пример проекции сил.
F При равновесии сумма проекций сил равна нулю: F1x + F2x + F3х = 0.
|
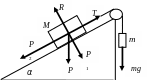
Действие трех сил на тело.
Действующие силы: тяжести P = Mg, натяжения нити Т = mg, реакции (ограничивают движение тела) R. P2 = Psinα = Mgsinα Равновесие обеспечивается при Т = Р2, R = Р1. Тогда условие равновесия: Mgsinα = mg, Msinα = m. |
Вращение тела вокруг жесткой оси.
Е сли
сила F
не проходит через ось вращения – на
тело действует сила вращения. Сила F1,
которая проходит через ось вращения
тела уравновешивается силой реакции
R = F2.
Вращение – только под действием силы
F1,
перпендикулярной линии, проходящей
через точку А
приложения силы и ось вращения О.
сли
сила F
не проходит через ось вращения – на
тело действует сила вращения. Сила F1,
которая проходит через ось вращения
тела уравновешивается силой реакции
R = F2.
Вращение – только под действием силы
F1,
перпендикулярной линии, проходящей
через точку А
приложения силы и ось вращения О.
Для равновесия тела, закрепленного на оси, существенен не сам модуль силы, а произведение модуля на расстояние (плечо) – момент силы относительно оси: M = F1r. Если момент равен нулю – сила не вызывает вращения.
Уравнение движения материальной точки (системы точек) определяет связь ускорения ai и силы Fi и записывается в соответствии со вторым законом Ньютона:
mi![]() ,
i
= 1,. . ., N,
,
i
= 1,. . ., N,
где
mi
- масса материальной точки, t
>
0 – время,
![]() - ее радиус-вектор,
- ее радиус-вектор,
![]() i
- результирующая всех действующих на
нее сил. Через
обозначено множество координат всех
точек системы.
i
- результирующая всех действующих на
нее сил. Через
обозначено множество координат всех
точек системы.
Величины i считаются заданными и могут зависеть как от времени, так и от пространственных координат и скоростей всех рассматриваемых точек.
Силу, как и любой вектор, можно спроектировать на любую ось. Проекция вектора на ось равна разности координат начала и конца отрезка:
m![]() ,
m
,
m![]() ,
m
,
m![]() .
.
Различают два вида движения: поступательное и вращательное.
Динамика поступательного движения.
При рассмотрении поступательного движения твердого тела его можно заменить материальной точкой, совпадающей с центром инерции тела, обладающей всей его массой и движущегося под действием главного вектора внешних сил, приложенных к телу..
Основной закон динамики поступательного движения: производная по времени от количества движения К материальной точки или системы точек относительно неподвижной (инерциальной) системы отсчета равна главному вектору всех внешних сил, приложенных к системе: dK/dt = F, или mас = F, где ас – ускорение центра инерции системы, - m ее масса.
В прямоугольных декартовых координатах уравнение движения имеет вид:
dKx/dt = Fх, dKy/dt = Fy, dKz/dt = Fz.
или
mi![]() = Fiх,
mi
= Fiх,
mi![]() = Fiу,
mi
= Fiу,
mi
![]() = Fiz.
= Fiz.
Простейшие случаи поступательного движения твердого тела.
а )
Движение по инерции (F
= 0) – равномерно поступательное движение
(с постоянной скоростью):
)
Движение по инерции (F
= 0) – равномерно поступательное движение
(с постоянной скоростью):
mv = const, а = 0. v = const, S = vt.
б) Движение под действием постоянной силы – равномерно ускоренное движение (с постоянным ускорением):
![]()
 (mv) = F = const,
mv = F
t + mv0,
(mv) = F = const,
mv = F
t + mv0,
где mv0 - количество движения тела в начальный момент времени t = 0.
Ускорение a = ∆v/∆t – отношение изменения скорости к потребовавшемуся для этого времени (время, за которое происходит изменение скорости).
Из состояния покоя изменение скорости к моменту t:
v
= at. Тогда S
= vt / 2 = at2/2,
v =
![]() .
.
Свободное
падение – частный случай равномерно
ускоренного движения без начальной
скорости. Ускорение этого движения
равно ускорению свободного падения a
= g.
Приняв s
= h, v
=
![]() .
.
Тело брошено вертикально вверх с начальной скоростью v0: hmax = v02/2g.
Работа = Сила х Перемещение.
П ри
F
= const
(в случае постоянной силы в процессе
перемещения) A
= F
s,
в случае переменной силы – интеграл от
силы по перемещению A
=
ри
F
= const
(в случае постоянной силы в процессе
перемещения) A
= F
s,
в случае переменной силы – интеграл от
силы по перемещению A
=
![]() .
.
Если тело движется в направлении действия силы тяжести, то над телом совершается работа A = mg h.
Чтобы поднять тело (увеличить расстояние от центра Земли), над ним следует совершить работу. Работа, совершаемая силой F при движении против силы тяжести (подъеме тела) на высоту h не зависит от пути – зависит только от того, насколько тело может опуститься до заданного уровня. Эта работа запасается в виде потенциальной энергии тела (энергии положения) A =Wп = mgh, равной работе, затраченной на подъем тела.
Это
не полная потенциальная энергия –
только приращение энергии при подъеме
тела на высоту (начало отсчета выбирается
произвольно). С учетом изменения
гравитационного поля по высоте Wп
= m![]() .
.
Потенциальной энергией называется энергия, зависящая только от взаимного расположения материальных точек (или тел).
Во всех физических явлениях важна не сама потенциальная энергия, а ее изменение, которым определяется совершаемая работа. Уровень отсчета изменений заранее оговаривается.
При подъеме на высоту накопилась потенциальная энергия Wп, при падении с этой высоты эта потенциальная энергия превратилась в кинетическую Wк. Wп = Wк = mgh = mv2/2.
Т ело
брошено горизонтально с начальной
скоростью v0
– комбинация двух
движений взаимно перпендикулярных друг
другу: горизонтального (равномерного
прямолинейного) и вертикального
(свободного падения).
ело
брошено горизонтально с начальной
скоростью v0
– комбинация двух
движений взаимно перпендикулярных друг
другу: горизонтального (равномерного
прямолинейного) и вертикального
(свободного падения).
Координаты каждой точки траектории:
- перемещение тела в горизонтальном направлении x = v0 t;
- перемещение тела в вертикальном направлении (равномерно ускоренное движение с ускорением g) y = gt2/2.
Из этих уравнений движения: t = x / v0 , y = gx2 / 2v0 – парабола.
в) Неравномерно ускоренное движение
dS
= Vdt.
S
=
![]() .
.
Математическая модель механического движения представляет собой систему дифференциальных уравнений относительно координат и скоростей движущегося объекта.
Процесс составления дифференциального уравнения по условию задачи (физической, технической) состоит в выражении на математическом языке связи между переменными величинами и их бесконечно малыми приращениями. Модели, описываемые обыкновенными дифференциальными уравнениями, в которых неизвестные функции зависят только от одной переменной - обыкновенные дифференциальные модели.
Ответы на вопросы, поставленные при построении дифференциальной модели, получают после интегрирования дифференциальных уравнений. С математической точки зрения задача свелась к задаче Коши для системы обыкновенных дифференциальных уравнений первого порядка с заданными начальными условиями. Задача Коши (задача с начальными условиями) – задача о нахождении частного решения, которое удовлетворяет n частным условиям y(x0) = y0, y’(x0) = y’0,…, y(n-1)(x0) = y(n-1) 0. Существование и единственность задачи Коши, методы ее решения известны из теории дифференциальных уравнений.
Тело, брошенное под углом к горизонту движется, как и в случае горизонтально брошенного тела, в результате комбинации двух движений: равномерного прямолинейного движения под углом к горизонту и свободного падения в вертикальном направлении (под действием только силы тяжести – без реакции опоры).
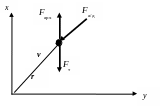 В
двумерной постановке тело, брошенное
под углом к горизонту, рассматривается
как материальная точка, движущаяся под
действием лишь одной силы - постоянной
силы его веса Р, направленной
вертикально вниз. Начало координат –
в точке приложения силы, обеспечившей
начальную скорость полета.
В
двумерной постановке тело, брошенное
под углом к горизонту, рассматривается
как материальная точка, движущаяся под
действием лишь одной силы - постоянной
силы его веса Р, направленной
вертикально вниз. Начало координат –
в точке приложения силы, обеспечившей
начальную скорость полета.
|
|
Тело массы m, брошенное под углом к горизонту, движется под действием постоянной силы веса Р = Fт, направленной вертикально вниз Р = mg.
Уравнения движения можно представить как в векторной, так и в координатной форме.
Для произвольной точки М (х,у) траектории тела:
mv = Р t + mv0, или v = gt + v0.
Проецируя векторные соотношения на оси координат, получим уравнения движения в координатной форме.
m dvx /dt = 0, vx = dx/dt,
m dvy /dt = - mg, vy = dy/dt
Необходимо найти зависимости x(t), y(t), vx(t), vy(t) из решения полученной системы дифференциальных уравнений при начальных условиях:
x(0) = x0, y (0) = y0, vx (0) = v0 cos Θ 0, vy (0) = v0 sin Θ 0.
Сопротивление воздуха
Cила сопротивления воздуха Fа/д (полная аэродинамическая сила) направлена противоположно вектору скорости тела прямо пропорциональна величине скоростного потока q и характерной площади тела S:
Fа/д = - CrqS, q = ρv2/2,
где Cr - коэффициент сопротивления, зависящий от свойств среды и тела, скорости потока, ρ [кг/м3] – плотность воздуха, зависит от высоты.
Коэффициент сопротивления определяется опытным путем, и для приближенных расчетов для тела в форме шара может быть принят независимым от скорости потока и равным 0,25 (плюс – минус 0,05 – в зависимости от скорости).
Тогда система уравнений запишется в виде:
dvx /dt = Cr qS cos Θ / m, vx = dx/dt,
dvy /dt = Cr qS sin Θ / m - g, vy = dy/dt
ρ = ρ (y), α = arctg vx / vy, q = ρv2/2
при начальных условиях:
x (0) = x0, y (0) = y0,
vx (0) = v0 cos Θ 0, vy (0) = v0 sin Θ 0.
Зависимость ρ = ρ (y) может быть задана в табличном или в аналитическом виде.
Задача не имеет аналитического решения и решается численным интегрированием. Определяется влияние шага интегрирования на точность решения задачи.
Изменение с высотой величины ускорения силы тяжести Земли
Ускорение свободного падения одинаково для всех тел и, также как и вес, зависит от географической широты и высоты над уровнем моря.
Стандартное (нормальное) значение ускорения свободного падения на уровне моря составляет g0 = 9,81 м/сек2. Для определения ускорения при удалении от поверхности Земли на высоту h используется формула g = g0[R0/(R0 + h)]2, R0 = 6370 км - радиус Земли. На географических полюсах (φ = 900) Fц = 0 и вес тела равен силе притяжения его к Земле. Вследствие того, что центростремительная сила зависит от широты, вес тела максимален на полюсах и минимален на экваторе, различие не превышает 0,55%.
Величина выталкивающей силы (закон Архимеда)
На тело действует выталкивающая сила воды в соответствии с законом Архимеда.
По закону Архимеда выталкивающая сила равна Fарх = g(y)Vρ0(y). Здесь Vρ0(y) – масса вытесненного воздуха, V – объем тела.
Величины присоединенной массы
Присоединенная масса может быть определена по формуле: m = 0,5 Vρ0.
Изменения плотности атмосферы с высотой
Гипотеза о постоянстве плотности атмосферы (ρ0 = 1,225 кг/м3) с высотой полета изменяется ρ = ρ (h), где h – высота над уровнем моря [м]: ρ = ρ0- 0, 00014h.
Кривизны Земли
Для учета кривизны Земли необходимо строить новую математическую модель - начало системы координат помещается в центр Земли. В этом случае сила притяжения направлена в начало координат (а не перпендикулярно оси координат), и тип кривой полета становится другим (эллипс, а не парабола).

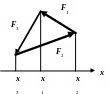 1x
= x1
– x2,
F2x
= x2
– x3,
F3х
= x3
– x1.
1x
= x1
– x2,
F2x
= x2
– x3,
F3х
= x3
– x1.