Завдання 5

Тема 5. Електромагнітна індукція.

Номер Вашого варіанта відповідає номеру Вашого прізвища в списку журналу групи (так варіанту 8 необхідно виконувати задачу 5.8, варіанту 11 – задачу 5.11 і т.д.).

5.1 Котушка має 100 витків дроту квадратного периметру із стороною квадрата 15 см, площа кожного з витків однакова і дорівнює площі квадратної рамки, загальний опір котушки рівний 1,5 Ом. Котушка знаходиться в однорідному магнітному полі, напрямленому перпендикулярно до площини котушки. Знайдіть значення індукованої в котушці е.р.с., якщо зовнішнє магнітне поле почне змінюватись лінійно від 0,1 до 0,6 Вб/м² за проміжок часу, рівний 1,5 с.

5.2 Плаский коловий виток дроту розміщений перпендикулярно до магнітного поля з індукцією В. Знайдіть закон зміни індукованої у витку е.р.с. Е з часом, якщо значення індукції магнітного поля змінюється з часом за законом В=В₀е^–at, де В₀= 9 мТл, а= 0,5 с^-1 і радіус витка r = 5 см. Чому дорівнює максимальне значення е.р.с. Е_m?

5.3 Закріплений з одного кінця (вісь обертання проходить через один з кінців стрижня), проводящий стрижень довжиною l = 0,5 м обертається із сталою кутовою швидкістю ω = 6,28 рад/с в однорідному магнітному полі з індукцією В = 0,2 Тл. Поле напрямлене перпендикулярно до площини обертання стрижня. Знайдіть е.р.с., індуковану між кінцями стрижня.

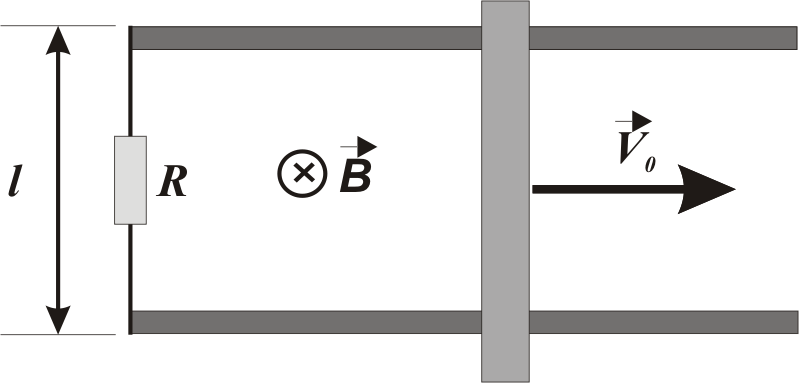
5.4-5.6 Перемичка масою m та довжиною l рухається без тертя по двом рейкам (Рис. 5.1) в однорідному магнітному полі з індукцією В, напрямленому за площину рисунка. Після надання перемичці початкової швидкості V₀ вправо її відпустили. Знайдіть швидкість перемички V(t), струм I(t) у колі та індуковану в колі е.р.с. E(t) як функції часу. Рис. 5.1

Таблиця 5.1

Варіанти	m, кг	l, м	R, oм	B, Тл	V0, м/c
4	0,4	0,6	4,0	0,5	6,0
5	0,5	0,7	5,0	1,0	5,0
6	0,6	0,8	6,0	1,5	4,0

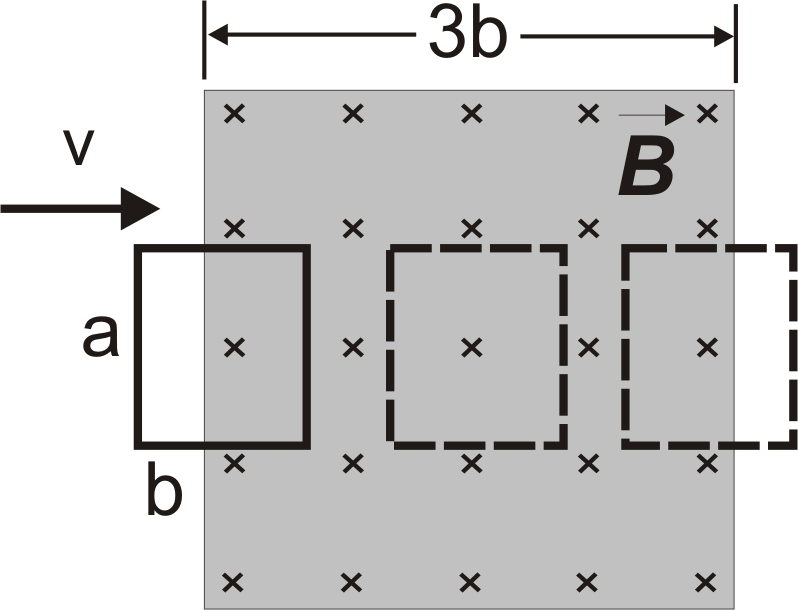
5.7 Прямокутна рамка із сторонами a та b і опором R рухається вправо (Рис. 5.2) із сталою швидкістю v. Рамка продовжує рухатись із цією швидкістю через область з однорідним магнітним полем з індукцією В, напрямленим за площину рисунку. Ширина області з однорідним магнітним полем дорівнює трьом сторонам рамки 3b. Побудуйте графіки залежності магнітного потоку Ф(х) через рамку в залежності від положення рамки, індукованої в рамці Е(х) е.р.с. в залежності від положення рамки, а також зовнішньої сили F_x(x), діючої на рамку в залежності від положення рамки. Вісь х вважати паралельною стороні b рамки та напрямленою також вправо. Рис. 5.2

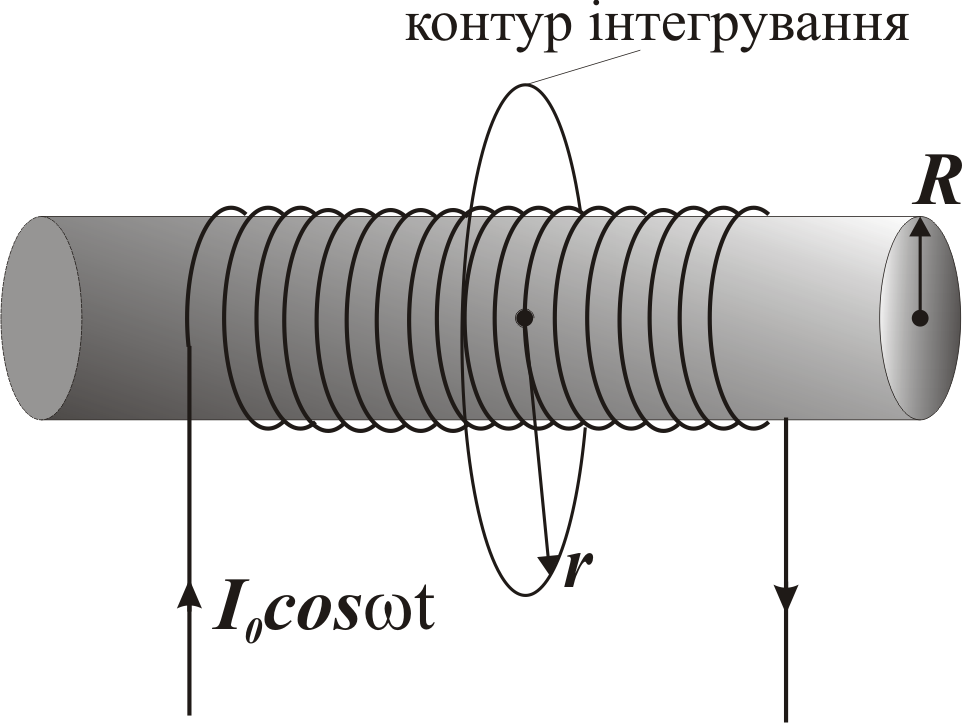
5.8-5.11 Довгий соленоїд (Рис. 5.3) радіусу R має n витків на одиницю довжини. По обмотці соленоїда тече змінний з часом синусоїдальний струм I = I₀ cosωt, де І₀ це максимальне значення струму і ω – циклічна частота джерела струму. Знайдіть електричне поле за межами (=1) соленоїда Е(r) на відстані r  R від його осі та всередині (1) соленоїда для значень 0  r  R. Побудуйте графік залежності Е(r) для моменту часу t=1 с для відстаней r = 0,0R; 0,3R; 0,6R; R; 1,1R; 1,2R; 1,4R; 1,6R; 1,9R; 2,5R; 4R. Таблиця 5.2 Рис. 5.3

Варіанти	І0, А	n, вит/м	R, см	ω, рад/с	
8	10,0	600	7,0	/6	700
9	13,0	570	8,0	/4	800
10	16,0	540	9,0	/3	900
11	20,0	500	10,0	/2	1000

5.12 Генератор змінного струму складається з N = 10 витків дроту кожен площею S= 0,1 м² та загальним опором R = 20 Ом, що обертаються в магнітному полі з індукцією В = 446 мТл із сталою частотою  = 50 Гц. Знайдіть максимальне значення індукованої е.р.с. Е_max та максимальне значення індукованого струму I_max. Запишіть закони зміни з часом індукованої е.р.с. Е(t) та індукованого струму I(t) для випадку коли на вихідні клемми під’єднаний провідник з малим опором.

5.13-5.15 По довгому соленоїду (Рис. 5.4), що має n витків на метр тече змінний з часом струм I = I₀(1 – e^-t). Всередині соленоїда (=1) коаксіально з ним розміщена котушка з радіусом R, що має N витків тонкого дроту. Яку е.р.с. індукує в котушці змінний струм? Рис. 5.4

Таблиця 5.3

Варіанти	n, вит/м	N, витків	I0, A	, с-1	R, cм
13	400	200	25	0,8	6,0
14	450	250	30	1,3	5,0
15	500	300	35	1,8	4,0

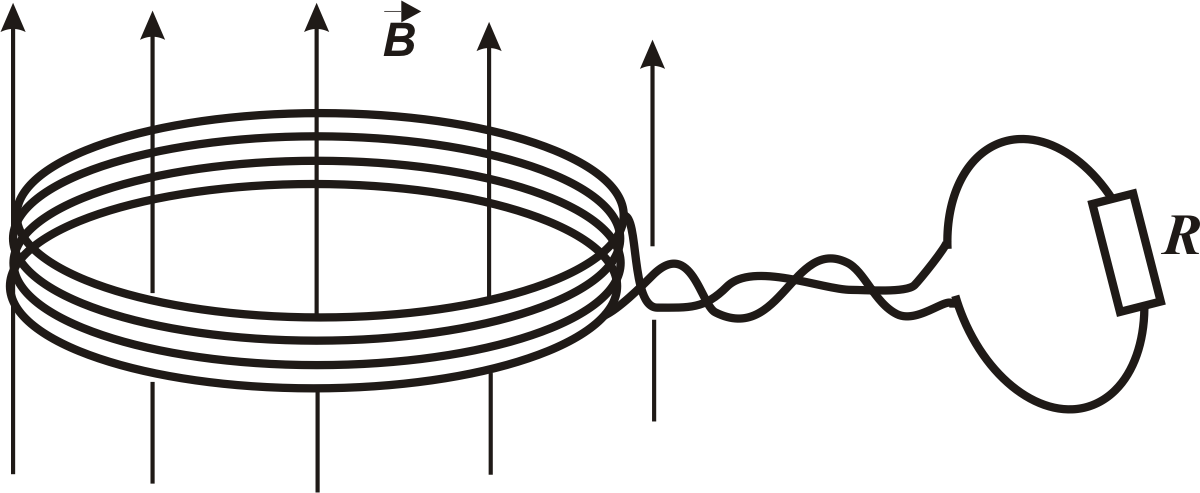
5.16-5.17 Колова котушка з площею витка рівною S виконана з N витків мідного дроту (Рис. 5.5) знаходиться в однорідному магнітному полі з індукцією В, напрямленому перпендикулярно (вгору) до площини котушки. Напрямок магнітного поля змінюють на зворотній. Знайдіть кількість електрики Q, що протікає через резистор з опором R, під’єднаний Рис. 5.5

до котушки, за час, на протязі якого напрямок магнітного поля змінюють на зворотній.

Таблиця 5.4

Варіанти	S, см2	N, витків	В, Тл	R, Ом
16	150	200	1,5	6,0
17	200	250	2,0	8,0

5.18-5.20 Квадратна котушка (Рис. 5.6) має N витків дроту і обертається навколо вертикальної осі, здійснюючи n обертів за хвилину. Горизонтальна складова магнітного поля Землі в околі котушки дорівнює 210^-5 Тл. Розрахуйте максимальне значення е.р.с. Е_max в котушці індуковане магнітним полем Землі.

Таблиця 5.5

Варіанти	n, об/хв	N, витків	а, cм
18	1000	200	10
19	1500	250	20
20	2000	300	30

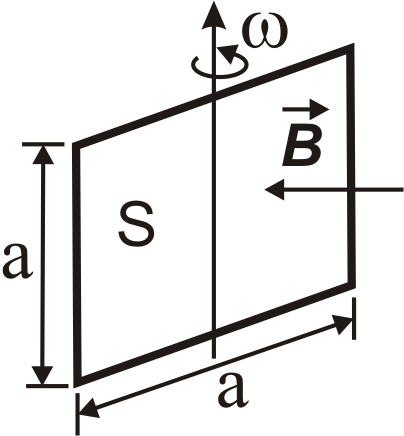Рис. 5.6

5.21-5.23 Перемичка масою m та довжиною l рухається без тертя по двом рейкам (Рис. 5.1) в однорідному магнітному полі з індукцією В, напрямленому за площину рисунка. Після надання перемичці початкової швидкості V₀ вправо її відпустили. Знайдіть швидкість перемички V(t), струм I(t) у колі та індуковану в колі е.р.с. E(t) як функції часу.

Таблиця 5.6

Варіанти	m, кг	l, м	R, oм	B, Тл	V0, м/c
21	0,5	0,7	5,0	0,6	4,0
22	0,6	0,8	6,0	1,1	3,0
23	0,7	0,9	7,0	1,6	2,0

5.24-5.27 Довгий соленоїд (Рис. 5.3) радіусу R має n витків на одиницю довжини. По обмотці соленоїда тече змінний з часом синусоїдальний струм I = I₀ cosωt, де І₀ це максимальне значення струму і ω – циклічна частота джерела струму. Знайдіть електричне поле за межами (=1) соленоїда Е(r) на відстані r  R від його осі та всередині (1) соленоїда для значень 0  r  R. Побудуйте графік залежності Е(r) для моменту часу t=1 с для відстаней r = 0,0R; 0,3R; 0,6R; R; 1,1R; 1,2R; 1,4R; 1,6R; 1,9R; 2,5R; 4R. Таблиця 5.7

Варіанти	І0, А	n, вит/м	R, см	ω, рад/с	
24	11,0	610	6,0	/6	750
25	14,0	580	7,0	/4	850
26	17,0	550	8,0	/3	950
27	21,0	510	9,0	/2	1000

5.28 Котушка має 200 витків дроту квадратного периметру із стороною квадрата 10 см, площа кожного з витків однакова і дорівнює площі квадратної рамки, загальний опір котушки рівний 2,5 Ом. Котушка знаходиться в однорідному магнітному полі, напрямленому перпендикулярно до площини котушки. Знайдіть значення індукованої в котушці е.р.с., якщо зовнішнє магнітне поле почне змінюватись лінійно від 0,1 до 0,6 Вб/м² за проміжок часу, рівний 1,5 с.

5.29 Плаский коловий виток дроту розміщений перпендикулярно до магнітного поля з індукцією В. Знайдіть закон зміни індукованої у витку е.р.с. Е з часом, якщо значення індукції магнітного поля змінюється з часом за законом В=В₀е^–at, де В₀= 9 мТл, а= 0,5 с^-1 і радіус витка r = 5 см. Чому дорівнює максимальне значення е.р.с. Е_m?

5.30 Закріплений з одного кінця (вісь обертання проходить через один з кінців стрижня), проводящий стрижень довжиною l = 0,5 м обертається із сталою кутовою швидкістю ω = 6,28 рад/с в однорідному магнітному полі з індукцією В = 0,2 Тл. Поле напрямлене перпендикулярно до площини обертання стрижня. Знайдіть е.р.с., індуковану між кінцями стрижня.

12