Завдання 4

Тема 4. Магнітне поле у вакуумі та середовищі.

Номер Вашого варіанта відповідає номеру Вашого прізвища в списку журналу групи (так варіанту 3 необхідно виконувати задачу 4.3, варіанту 12 – задачу 4.12 і т.д.).

4.1−4.3 По прямолінійному залізному проводу з відносною магнітною проникністю μ та радіусом R (див. Табл. 4.1) тече струм величиною І. Густина струму по всьому перерізу проводу однакова. Визначити напруженість та індукцію магнітного поля всередині проводу (0≤х≤R) та в зовнішньому просторі навколо нього (x>R) як функцію відстані х від осі проводу. Побудувати графік залежності В=В(х) для значень х = 0,00; 0,25; 0,50; 0,75; 1,00; 1,25; 1,50; 1,75; 2,00; 2,25; 2,50; 2,75; 3,00; 3,25; 3,50; 3,75; 4,00 мм.

Таблиця 4.1

Варіанти	μ	R, мм	І, А
1	150	1,5	0,15
2	200	2,0	0,20
3	250	2,5	0,25

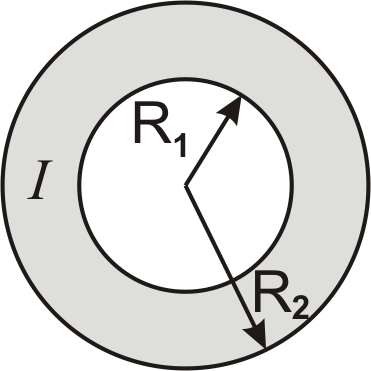
4.4−4.6 По прямолінійному проводу циліндричної форми (рис. 4.1) з відносною магнітною проникністю μ=1 та внутрішнім R₁ і зовнішнім R₂ радіусами тече сталий струм величиною І. Густина струму по всьому перерізу проводу однакова. Визначити напруженість магнітного поля всередині проводу (0≤х≤R₁; R₁≤х≤R₂ ) та в зовнішньому просторі навколо нього (x≥R₂) як функцію відстані х від осі проводу. Побудувати графік залежності Н=Н(х) для значень х = 0,00; 0,25; 0,50; 0,75; 1,00; 1,25; 1,50; 1,75; 2,00; 2,25; 2,50; 2,75; 3,00; 3,25; 3,50; 3,75; 4,00; 4,25; 4,50; 4,75; 5,00; 5,25; 5,50; 5,75; 6,00; 6,25 мм.

Варіанти	R1, мм	R2, мм	І, А
4	1,5	2,5	0,15
5	2,0	3,5	0,20
6	2,5	4,5	0,25

Таблиця 4.2 Рис. 4.1

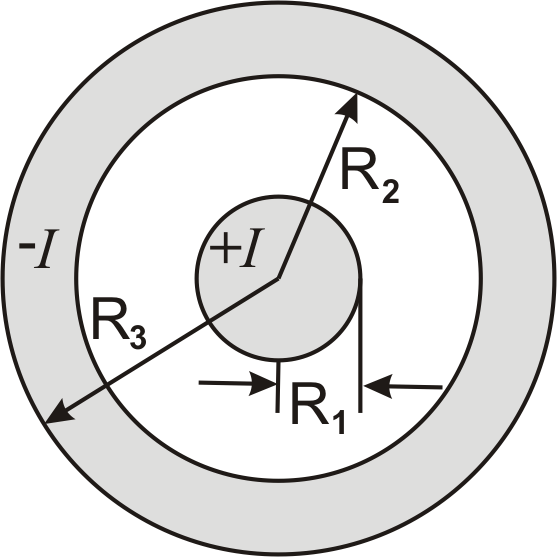4.7−4.10 На рис. 4.2 зображено переріз коаксіального кабелю по якому течуть струми −І та +І, густина струму по перерізу провідників однакова. Відносна магнітна проникність ізоляції і матеріалу провідників однакова і дорівнює 1. Розміри перерізу коаксіального кабелю та величина струму наведені в таблиці 4.3. Визначити напруженість магнітного поля всередині проводу (0≤х≤R₁; R₁≤х≤R₂; R₂≤х≤R₃) як функцію відстані х від осі проводу. Побудувати графік залежності Н=Н(х) для значень х = 0,00; 0,25; 0,50; 0,75; 1,00; 1,25; 1,50; 1,75; 2,00; 2,25; 2,50; 2,75; 3,00; 3,25; 3,50; 3,75; 4,00; 4,25; 4,50; 4,75; 5,00; 5,25; 5,50; 5,75; 6,00; 6,25 мм. Рис. 4.2 Таблиця 4.3

Варіанти	R1, мм	R2, мм	R3, мм	І, А
7	1,25	4,50	5,50	0,2
8	1,50	4,75	5,75	0,3
9	1,75	5,00	6,00	0,4
10	2,00	5,25	6,25	0,5

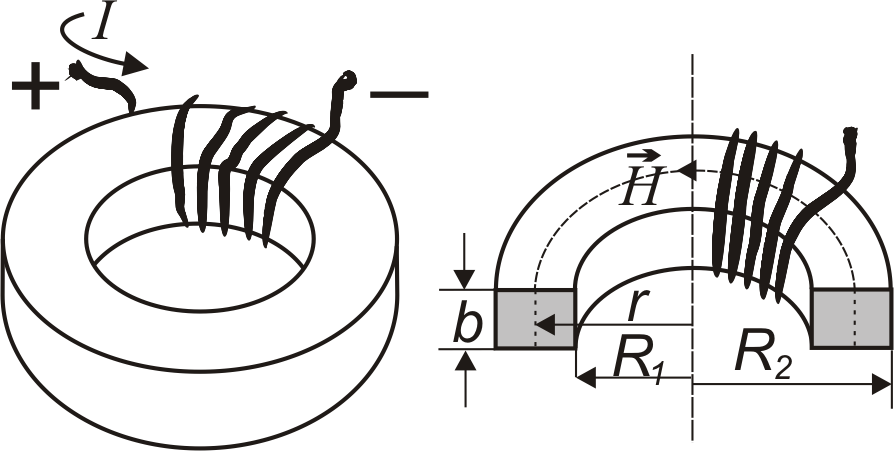4.11−4.15 Знайти індуктивність тороїда L, зображеного на рис. 4.3, якщо його магнітна проникність μ значно перевищує зовнішню. Геометричні розміри тороїда b, R₁, R₂, кількість витків n та значення відносної магнітної проникності μ надані в таблиці 4.4.

(Магнітний потік за заданої умови фактично зосереджений в тороїді).

Рис. 4.3

Таблиця 4.4

Варіанти	b, мм	R1, мм	R2, мм	n	μ
11	6	25	45	5	150
12	7	30	50	6	140
13	8	15	35	7	130
14	9	20	40	8	120
15	10	15	30	9	110

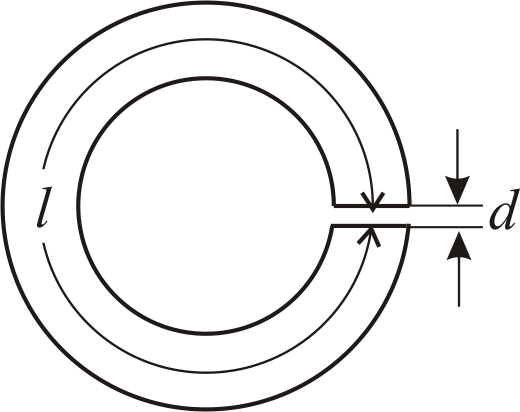
4.16−4.20 Визначити індуктивність тороїда (рис. 4.4), якщо в ньому зробили вузький проріз d. Магнітне поле вважати однорідним. Площа одного витка S, кількість витків n, відносна магнітна проникність тороїда μ, значення l та d наведені в таблиці 4.5.

Таблиця 4.5

Варіанти	S, см2	n	μ	l, см	d, мм
16	2,0	9	100	96	1,32
17	1,8	8	110	84	1,94
18	1,6	7	120	69	1,15
19	1,4	6	130	47	1,23
20	1,2	5	140	25	1,32

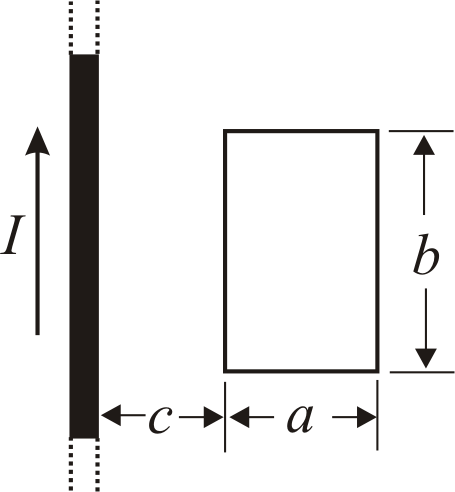Рис. 4.4

4.21−4.23 На рис. 4.5 зображений прямокутний контур шириною а та довжиною b, який знаходиться на відстані с від нескінченно довгого прямолінійного струму І і лежить з ним в одній площині. Сторона b контура паралельна до прямолінійного струму. Знайдіть повний магнітний потік через прямолінійний контур. Значення I, a, b та c наведені в таблиці 4.6.

Таблиця 4.6

Варіанти	І, А	a, см	b, см		с, см
21	0,5	2,0	4,0		2,0
		22		1,0		3,0		5,0	2,5
		23		1,5		4,0		6,0	3,0

Рис. 4.5

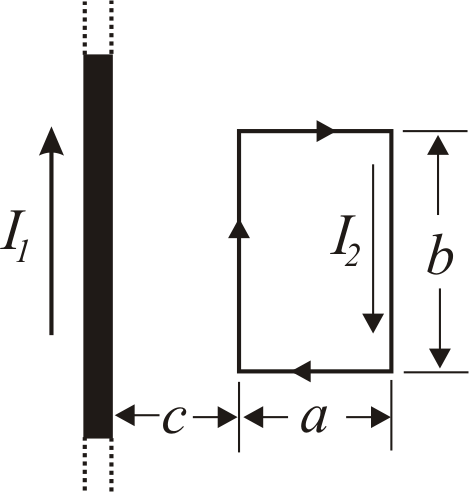4.24−4.26 Знайдіть магнітну силу F, що діє на верхню частину (сторона а із струмом зліва направо) прямокутного контура, зображеного на рис. 4.6. Прямокутний контур із струмом І_2, шириною а та довжиною b, який знаходиться на відстані с від нескінченно довгого прямолінійного струму І₁ і лежить з ним в одній площині, має сторону b контура паралельну до прямолінійного струму І₁. Значення I₁, I₂, a та c наведені в таблиці 4.7.

Таблиця 4.7

Варіанти	І1, А	І2, А	a, см	с, см
24	1,0	2,0	5,0	2,0
25	2,0	1,5	4,0	3,0
26	0,5	1,0	3,0	1,0

Рис. 4.6

4.27−4.30 Знайдіть результуючу магнітну силу F, що діє на прямокутну рамку із струмом І_2, що знаходиться в магнітному полі нескінченно довгого прямолінійного струму І₁ і лежить з ним в одній площині (рис 4.6). Значення I₁, I₂, a, b та c наведені в таблиці 4.8.

Таблиця 4.8

Варіанти	І1, А	І2, А	a, см	b, см	с, см
27	2,0	4,0	2,0	3,0	1,0
28	3,0	3,0	3,0	4,0	1,5
29	4,0	2,0	4,0	5,0	2,0
30	5,0	1,0	5,0	6,0	2,5