2.6 Аппроксимация моделью второго порядка

2.6.1 Аппроксимация двумя инерционными звеньями первого порядка с разными постоянными времени

Для данной аппроксимации можно выбрать передаточную функцию второго порядка с запаздыванием τ_м и различными постоянными времени.

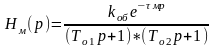, (2.6.1)

Постоянные времени Т_о1 и Т_о2 определяются по некоторым характерным точкам переходного процесса.

В большинстве случаев модель обеспечивает достаточную точность для практических расчетов, если принять Т_о1 /Т_о2 = 0,5 при этом постоянные времени Т_о1 и Т_о2 определяются следующим образом по ординате:

h(t₂) = 0,63·К_об, (2.6.2)

h(t₂) = 0,63·9;

h(t₂) = 5,67;

t₂ = 81.

Рассчитываем Т_о1 и Т_о2 , с:

Т_о2 = 0,64·t _, (2.6.3)

Т_о2 = 0,64·81= 51,84;

Т_о2 = 51,84;

Т_о1 = 0,5·Т_о , (2.6.4)

Т_о1 = 0,5·51,84= 25,92;

Т_о1 = 25,92;

Полученные значения Т_о1 и Т_о2 задаются в программе ТАУ-3 Linsys. Полученный переходный процесс оцифровывается по тому же принципу, что и исходная кривая разгона. Полученный переходный процесс представлен на рисунке 2.11.

Ряд 1-переходный процесс объекта,

Ряд 2-аппроксимация объекта.

Рисунок 2.6.1 - Аппроксимация переходной характеристика реального объекта моделью второго порядка с разными постоянными времени

2.6.2 Аппроксимация двумя инерционными звеньями первого порядка с одинаковыми постоянными времени

Модель второго порядка с одинаковыми постоянными времени и запаздыванием имеет вид:

. (2.6.5)

Т_оi = T_об /2,72 , (2.6.6)

Т_оi = 82/2,72= 30,14706;

Т_оi = 30,14706.

Полученные значения Т_оi задаются в программе ТАУ-3 Linsys. Полученный переходный процесс оцифровывается по тому же принципу, что и исходная кривая разгона. Полученный переходный процесс представлен на рисунке 2.6.2.

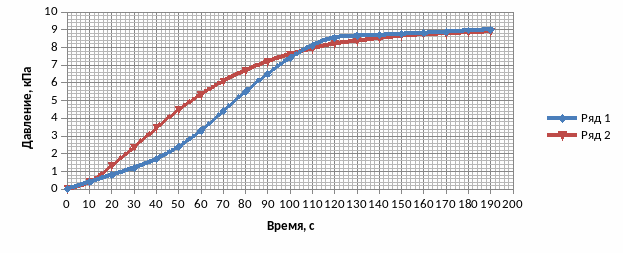
Ряд 1-переходный процесс объекта,

Ряд 2-аппроксимация объекта.

Рисунок 2.6.2- Аппроксимация переходной характеристики двумя моделями первого порядка с одинаковыми постоянными времени

2.7 Определение оптимальной передаточной функции

Критерием выбора выбирается квадратичный интегральный критерий качества, характеризующий суммарную площадь, ограниченную кривой переходного процесса. Графики для сравнения переходных процессов представлены на рисунке 2.7.1.

Таблица 2.7-определение интегральной квадратичной ошибки для различных моделей аппроксимации

Время	Переходные функции обьектов и моделей				Вычисление ошибки
	Исходная	1 пор.	2 п. разл. Т	2 п. один Т		1 пор.		2 п.разл.Т		2 п. один Т
0	0	0	0	0		0		0		0
10	0,4	0	0,29	0,4		0,16		0,0121		0
20	0,8	0	0,91	1,31		0,64		0,0121		0,2601
30	1,2	0,143941627	1,71	2,36		1,115259286		0,2601		1,3456
40	1,7	1,429134744	2,6	3,44		0,073367987		0,81		3,0276
50	2,4	2,527820356	3,44	4,47		0,016338043		1,0816		4,2849
60	3,3	3,467064473	4,24	5,33		0,027910538		0,8836		4,1209
70	4,4	4,270005279	4,93	6,09		0,016898627		0,2809		2,8561
80	5,5	4,956423142	5,58	6,69		0,295475801		0,0064		1,4161
90	6,5	5,543227894	6,09	7,2		0,915412862		0,1681		0,49
100	7,4	6,044875414	6,58	7,6		1,836362644		0,6724		0,04
110	8,1	6,473723736	6,96	7,93		2,644774486		1,2996		0,0289
120	8,55	6,840337497	7,31	8,2		2,922945874		1,5376		0,1225
130	8,65	7,153748189	7,58	8,36		2,238769482		1,1449		0,0841
140	8,69	7,421676653	7,82	8,51		1,608644112		0,7569		0,0324
150	8,75	7,65072328	8,04	8,64		1,208409306		0,5041		0,0121
160	8,81	7,846530611	8,2	8,73		0,928273263		0,3721		0,0064
170	8,87	8,01392234	8,33	8,78		0,73286896		0,2916		0,0081
180	8,95	8,157022144	8,44	8,84		0,62881388		0,2601		0,0121
190	9	8,279355274	8,56	8,89		0,519328821		0,1936		0,0121
Ошибка					σ1		σ2р		σ2о
						18,52985397		10,5478		18,16

Интегральная квадратичная ошибка вычисляется по формуле:

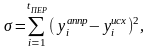(2.7.1)

Для данной системы регулирования выбирается аппроксимация двумя инерционными звеньями первого порядка с разными постоянными времени, так как у неё наименьшая квадратичная ошибка.

Ряд 1- реальный переходный процесс

Ряд 2-аппроксимация моделью первого порядка

Ряд 3-аппроксимация двумя инерционными звеньями первого порядка с разными постоянными времени

Ряд 4- аппроксимация двумя инерционными звеньями первого порядка с одинаковыми постоянными

Рисунок 2.7.1 - Графики сравнения переходных процессов