1.5. Квадратичные формырегулярнойповерхности
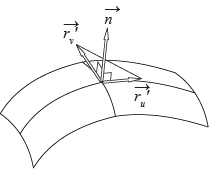
Положение касательной плоскости удобно характеризовать с помощью единичного вектора
перпендикулярного к этой плоскости.
При этом вектор
называют нормалью регулярной поверхности.
Первой квадратичной формой регулярной поверхности называют квадрат полного дифференциала векторной функции, определяющей поверхность:
Первая квадратичная форма регулярной поверхности определяется особыми коэффициентами:
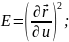
Если регулярная поверхность задана графиком
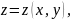
то
Определим длину регулярной кривой
на регулярной поверхности:
Говорят, что первая квадратичная форма задает метрику регулярной поверхности.
Направлением
в заданной точке регулярной поверхности
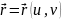
называется направление вектора
Угол между направлениями
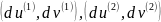
называется угол между соответствующими векторами
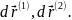
Определим этот угол:
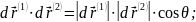
Направление регулярной кривой на регулярной поверхности в заданной точке – это направление вектора, касательного к кривой в точке.
Угол между регулярными кривыми на регулярной поверхности в заданной точке – это угол между направлениями кривых в точке.
Угол между координатными линиями регулярной поверхности
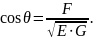
Координатная сеть на регулярной поверхности будет ортогональна, если
Площадьрегулярнойповерхности
Второй квадратичной формой регулярной поверхности называется взятое со знаком «-» скалярное произведение полного дифференциала векторной функции, определяющей поверхность, на полный дифференциал нормали поверхности:
Вторая квадратичная форма регулярной поверхности определяется своими коэффициентами:
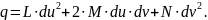
Другой способ определения коэффициентов второй квадратичной формы:
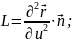
Если регулярная поверхность задана графиком
то
1.6. Нормальная кривизна регулярнойповерхности
Если пересечь регулярную поверхность плоскостью, проходящей через нормаль в заданной точке, то в достаточно малой окрестности точки получим плоскую регулярную кривую пересечения. Кривизна этой кривой пересечения называется нормальной кривизной регулярной поверхности в заданной точке в направлении кривой пересечения.
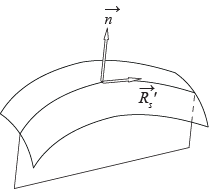
Теорема Менье: произведение кривизны регулярной кривой регулярной поверхности в заданной точке на косинус угла между главной нормалью кривой и нормалью поверхности есть нормальная кривизна поверхности в направлении кривой:
Доказательство.
Пусть
‑этонормальповерхности, а
‑ это главная нормаль кривой, тогда в соответствии с первой формулой Френе имеем:
Приэтом
С другой стороны
Правая часть зависит только от направления кривой и является кривизной соответствующего нормального сечения. Действительно, если
т. е. векторы
коллинеарны, то
Теорема доказана.
Следствие из теоремы:
Для изучения регулярной поверхности в малой окрестности заданной точки совместим с точкой начало отсчета декартовой системы координат. Ось
направим по нормали поверхности, а оси
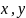
расположим в касательной плоскости.
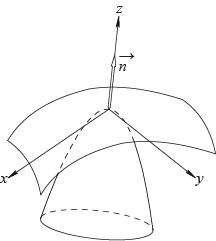
При этом саму поверхность в заданной малой окрестности представим графиком
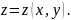
Разложим эту функцию в ряд Тейлора, пренебрегая бесконечно малой частью разложения:
График получившейся функции представляет собой параболоид, который называется соприкасающимся в заданной точке.
Надлежащим поворотом осей
вокруг оси
приводим уравнение соприкасающегося параболоида к виду
При этом направления осей
называются главными направлениями в заданной точке.
Нормальные сечения в этих направлениях называются главными нормальными сечениями, а кривизны этих сечений – главными нормальными кривизнами. Главные нормальные сечения представляют собой параболы с кривизнами
равными соответствующим главным нормальным кривизнам.
Если
то главная нормаль параболы совпадает с нормалью соприкасающегося параболоида, если же
то угол между этими нормалями равен 180°.
Теорема Эйлера: нормальная кривизна регулярной поверхности в заданной точке в направлении, составляющем угол
с первым главным направлением, равна
Доказательство.
Определяем коэффициенты первой и второй квадратичных форм:
Отсюда
Проведем нормальное сечение, составляющее с первым главным направлением угол
Приэтом
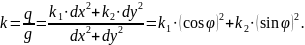
Теорема доказана.
Теорема: главные направления в заданной точке регулярной поверхности – это те направления, в которых нормальные кривизны достигают экстремумов.
Доказательство.
Пусть
Тогда
Отсюда
Ясно, что наибольшее значение
достигается при
а наименьшее при
следовательно экстремумы нормальных кривизн достигаются в главных направлениях и они равны соответственно
Если
то
В этом случае все направления главные.
Теорема доказана.
Следствия из теоремы:
1) если в заданной точке существуют два различных главных направления, то в такой точке главные нормальные кривизны не равны между собой;
2) если в заданной точке все направления главные, то в такой точке главные нормальные кривизны равны между собой.