2.11.4. Формообразованиеэвольвентного профиля долбяком

Рассмотрим передачу внешнего зацепления, составленную из эвольвентного цилиндрического колеса и инструмента в виде долбяка.

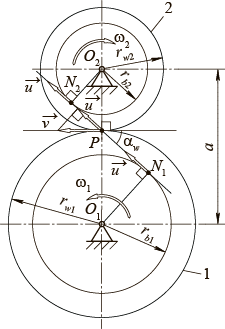
Колесо вращается с угловой скоростью

а долбяк‑ с угловой скоростью

Линия зацепления

в процессе обработки не изменяет своего положения, т. к. проходит через две неподвижные точки: полюс зацепления и точку касания с основной окружностью радиуса

Таким образом, угол зацепления, т. е. угол под которым линия зацепления пересекает касательную к начальным окружностям в полюсе зацепления,

Линия зацепления также касается окружности радиуса

которая жестко связана с долбяком. Данная окружность называется основной окружностью долбяка. В процессе обработки начальные окружности радиусами

обкатываются без проскальзывания. Скорость полюса

Учитывая, что

получаем

где

‑ это скорость линии зацепления, которая движется поступательно вдоль самой себя.Линия зацепления и основная окружность колесаобкатываются без проскальзывания. Это же справедливо и для пары линия зацепления - основная окружность долбяка.Движение линии зацепления относительно колеса, т. е. перекатывание без проскальзывания линии зацепления по мысленно остановленной основной окружности колеса, очевидно, приводит к образованию заданной эвольвенты определенной точкойлинии зацепления – точкой контакта профилей колеса и долбяка, взятой в определенный момент времени.

Но то же самое можно утверждать касательно долбяка. Следовательно, профиль долбяка представляет собой эвольвенту.

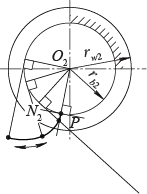
При изготовлении долбяка обеспечивают стандартное значение угла профиля на его делительной окружности:

При этом такое же значение угла профиля получается на делительной окружности колеса. Действительно, на соответствующих начальных окружностях шаги зубьев долбяка и колеса одинаковы и равны

откуда следует, что шаги зубьев долбяка и колесаодинаковы также и на соответствующих основных окружностях:

откуда, в свою очередь, следует, что

Угол зацепления находится следующим образом. Межосевое расстояние в станочном зацеплении колеса и долбяка

В итоге получаем

При этом межосевое расстояние может быть определено следующим образом:

где

‑ это радиус впадин обрабатываемого колеса, а

‑ радиус выступов долбяка.

Угол зацепления может быть найден другим способом. Шаг зубьев и долбяка, и колеса на соответствующих начальных окружностях равен

где

‑ это толщина зуба колеса на его начальной окружности, а

‑ толщина зуба долбяка на его начальной окружности.

При этом подразумевается т. н. беззазорное зацепление, когда толщина зуба долбяка равна ширине впадины колеса на соответствующих начальных окружностях и наоборот.

Имеем

Величина

задается на чертеже посредством коэффициента

смещения исходного контура, при этом

Величина

может быть определена при помощи измерения толщины

зуба долбяка на делительной окружности, при этом