1. Элементы дифференциальной геометрии
1.1. Векторные функции скалярного аргумента
Векторназывается векторной функцией скалярного аргумента, если каждому значению скаляра из области допустимых значений соответствует определенное значение вектора:
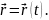
Вектор
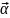
называется бесконечно малым, если его модуль стремится к нулю.
Производной векторной функции по ее скалярномуаргументуназывается предел отношения приращения вектора к соответствующему приращению аргумента, когда это приращение стремится к нулю:
Некоторые правила дифференцирования векторной функции по скалярному аргументу:
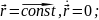
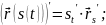
Докажем справедливость последнего правила.
Пусть
Если скалярному аргументу
дать приращение
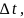
то векторные функции
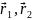
получат приращения
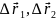
соответственно. При этом
откуда
Поделим обе части этого равенства на
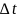
и перейдем к пределу при
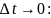
откуда и следует, что доказываемое правило справедливо.
Применительно к векторной функции скалярного аргумента рассматриваются также дифференциал
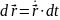
и интегралы, в частности определенный интеграл
Если векторную функцию скалярного аргумента рассматривать в декартовой системе координат, то
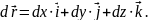
1.2. Понятие кривой
Кривую опишем при помощирадиус-вектора
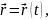
соединяющего произвольный фиксированный центр и точку, принадлежащую кривой.
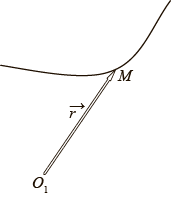
Кривая задается на промежутке
некоторой числовой оси.
Кривая называется регулярной, если во всех точках заданного промежутка
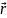
непрерывно дифференцируема и
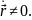
Пусть
‑точки, принадлежащиерегулярнойкривой и соответствующие параметрам
Прямая
называется направленной секущей кривой в точке
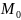
Направленной касательной к кривойвточке
называется предел направленных секущих в этой точкепри
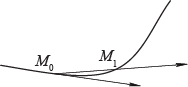
Теорема: в каждойточке регулярной кривой существует направленная касательная, определяемая направляющим вектором
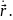
Доказательство.
Вектор
лежит на направленной секущей, проходящей через точки
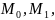
которым соответствуют радиус-векторы
Производная
Отсюда следует, что в точке
существует направленная касательная к кривой, которая определяется в пространстве вектором
Теорема доказана.
Длиной регулярной кривой называется предел длины ломаной, вписанной в кривую, при стремлении к нулю длины наибольшего сегмента ломаной.
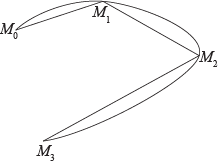
Теорема: всякая регулярная кривая имеет определенную длину. Более того, если регулярная кривая задана векторной функцией
тодлинакривой
Доказательство.
Впишем в кривую ломаную. Длина этой ломаной
где
При этом
Согласно теореме Лагранжа имеем
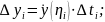
где
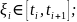
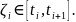
Отсюда
Перейдя к пределу, получим:
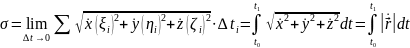
Теорема доказана.
Следствие из теоремы:
Введем такой скалярный аргумент радиус-вектора
точкирегулярнойкривой, как длина дуги
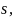
отсчитываемая от некоторого центра, взятого на кривой.
Данный аргументназывается естественным.
Теорема: имеет место соотношение:
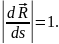
Доказательство.
Имеем:
Учитывая, что
получаем
Теорема доказана.