1. Закон кулона. Напряжённость электростатического поля. Теорема гаусса Основные формулы

Закон сохранения заряда в замкнутой системе

Q₁+Q₂+…+Q_n=const.

Закон Кулона

,

где k=9^.10⁹ м/Ф; F – сила взаимодействия двух точечных зарядов Q₁ и Q₂; r – расстояние между зарядами; ε – диэлектрическая проницаемость среды.

Напряженность электростатического поля

,

где – сила, действующая на точечный положительный заряд Q₀, помещенный в данную точку поля.

Напряжённость электростатического поля точечного заряда Q на расстоянии r от заряда

.

Поток вектора напряженности электростатического поля:

а) через площадку dS: ;

б) через замкнутую поверхность S: ,

где – вектор, модуль которого равен dS, а направление совпадает с нормалью к площадке; Е_n – проекция вектора на нормаль к площадке dS.

Принцип суперпозиции электростатических полей

,

где – напряженность поля, создаваемого зарядом Q_i .

Плотность зарядов (линейная τ, поверхностная σ, объемная ρ)

.

Теорема Гаусса для электростатического поля:

а) в случае дискретного распределения зарядов

;

б) в случае непрерывного распределения зарядов

,

где Е_n – проекция вектора на нормаль к площадке dS; – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S; n – число зарядов; Ф/м – электрическая постоянная.

В случае диэлектрика и – свободные заряды внутри замкнутой поверхности S.

Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью,

,

где σ – поверхностная плотность заряда.

Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом R с зарядом Q на расстоянии r от центра сферы,

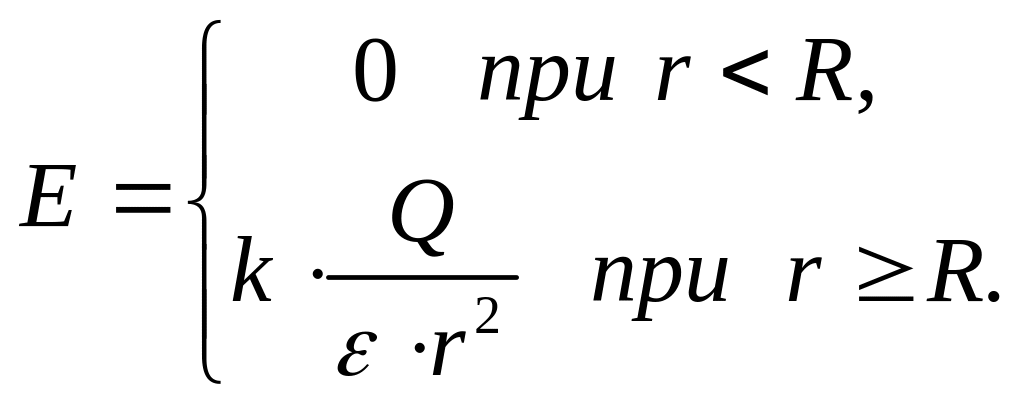
Напряженность поля, создаваемого равномерно заряженным бесконечным цилиндром радиусом R на расстоянии r от оси цилиндра,

Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура L

,

где – проекция вектора на направление элементарного перемещения .

Примеры решения задач

Пример 1

Два заряда Q₁ = 27 мкКл и Q₂ = -64 мкКл расположены на расстоянии 5 м друг от друга. Найти напряженность электрического поля в точке, удаленной на расстоянии = 3 м от первого и = 4 м от второго заряда. Найти силу, действующую на заряд Q₃ = 2 мкКл, помещенный в точку А.

Дано: Q1 = 27 мкКл = 27.10-6 Кл Q2 = -64 мкКл = -64.10-6 Кл r = 5 м = 3 м = 4 м Q3 = 2 мкКл = 2.10-6 Кл

EA, F-?

Решение

По принципу суперпозиции электрических полей

.

Поскольку , то угол САВ = 90⁰. Следовательно, .

По теореме Пифагора , где ; .

В/м.

Сила F, действующая на заряд Q₃,

F = .

Ответ: E_A =

Пример 2

По полуокружности радиусом R = 0,1 м равномерно распределен заряд с линейной плотностью τ = 0,2 мкКл/м. Найти напряженность электрического поля в центре полуокружности.

Дано: R = 0,1 м τ = 0,2 мкКл/м = 0,2.10-6 Кл/м

E -?

Решение

Мысленно разобьем полуокружность на бесконечно малые дуги. Пусть dQ – заряд дуги dl, тогда . Напряженность dE поля, создаваемого зарядом dQ в точке O,

– угол, который опирается на дугу dl.

Разложим вектор на две составляющие вдоль осей ox и oy:

По принципу суперпозиции электрических полей . Но т.к. горизонтальные вклады в напряженность поля от зарядов dQ и dQ^’ симметрично расположенных относительно OY, взаимно компенсируются.

Тогда

= В/м.

Ответ: E = В/м.

Пример 3

Бесконечная плоскопараллельная пластина толщиной d = 0,2 м равномерно заряжена по объему с плотностью электрического заряда ρ = 4 нКл/м³. Найти напряженность электрического поля на расстоянии r₁ = 0,05 м от срединной плоскости пластины и напряженность поля вне пластины. Для пластины ε = 4.

Дано: d = 0,2 м ρ = 4 нКл/м3 = Кл/м3 r1 = 0,05 м

E1, E2 -?

Решение

1. Для применения теоремы Гаусса выберем в качестве замкнутой поверхности S₁ поверхность цилиндра высотой , который делится срединной плоскостью π пополам.

По теореме Гаусса . (1)

Вектор направлен от срединной плоскости π перпендикулярно пластине. Поэтому E_n=0 для всех точек боковой поверхности цилиндра и E_n=E₁=const для всех точек обоих оснований. Тогда формула (1) принимает вид

;

заряд , расположенный внутри цилиндрической поверхности S₁, .

Tогда

В/м.

2. Пусть S₂ – поверхность цилиндра, высота которого больше толщины d пластины и который делится пополам срединной плоскостью π.

По теореме Гаусса . (2)

E_n = 0 для точек боковой поверхности; E_n = E₂ = const для точек обоих оснований; Q_внутр= = – заряд пластины, находящийся внутри поверхности S₂; ε =1, т.к. оба основания цилиндра находятся вне пластины. Тогда по формуле (2)

В/м.

Ответ: Е₁ = 56,5 В/м, Е₂ = 45,2 В/м.

Пример 4

Вдоль диагонали куба с ребром 0,1 м. расположена длинная равномерно заряженная нить с линейной плотностью заряда 0,2 мкКл/м. Найти поток вектора напряженности электрического поля через поверхность куба.

Дано: а = 0,1 м τ = 0,2 мкКл/м = 0.2.10-6 Кл/м

ФЕ -?

Решение

По теореме Гаусса

,

где Q_внутр – заряд нити, расположенный внутри куба; – диагональ куба.

По теореме Пифагора ; , тогда .

.

Ответ: Ф_{Е .}

Пример 5

Показать с помощью теоремы Гаусса, что заряд заряженного проводника расположен лишь на поверхности проводника.

Решение

В ыберем замкнутую поверхность S внутри проводника, очень близко отстоящую от его поверхности.

По теореме Гаусса

.

Поскольку внутри проводника, а значит, во всех точках поверхности S. Тогда Этот результат справедлив для поверхности S внутри проводника, сколь угодно близко расположенной к его поверхности. Следовательно, избыточный заряд проводника находится только на его поверхности.