Дифракція рентгенівських променів. Формула Вульфа-Брегга

Відомо, що для якнайкращих умов спостереження дифракційної картини постійна решітки має бути того ж порядку, що і довжина падаючої хвилі. З іншого боку, у природі існують такі просторові структури – кристали, де атоми розміщені на відстанях близько см. Отже, кристал є тривимірною дифракційною решіткою, в якій неоднорідності (тобто атоми, молекули, іони) регулярно повторюються у трьох вимірюваннях. Роль щілини в даному випадку відіграє елементарний осередок кристала. Цей факт допоміг М.Лауе (1912 р.) прийти до висновку, що існуючі природні кристали з постійною близько см є дуже зручними тривимірними решітками для спостереження дифракції рентгенівських променів, що мають довжини хвиль того ж порядку. Подібні експерименти дозволили, вивчаючи дифракцію рентгенівських променів відомої довжини на просторових решітках (сукупність атомів або іонів, розташованих в кристалічних решітках на відстані близько см), визначити міжатомні відстані (постійні грати) в кристалічних решітках.

Суть ідеї Лауе при постановці відповідного експерименту полягає в наступному: кристал К розташований на підставці, освітлюють рентгенівським випромінюванням безперервного спектру, який випромінюється рентгенівською трубкою (рис.2.43а). Випромінювання з довжиною хвилі, сумірної з постійною кристалічної решітці, дифрагуючи на цій решітці, дає відповідну дифракційну картину (так звану лауеграмму). Аналіз лауе-грамми дозволяє отримати відомості про кристалічну структуру.

Можна вивести просту практичну формулу, що дає умову максимуму при дифракції від просторових решіток. Зупинимося|зупинятимемося| на виведенні цієї формули.

(а)

Рис.2.43

Формула Вульфа-Брегга

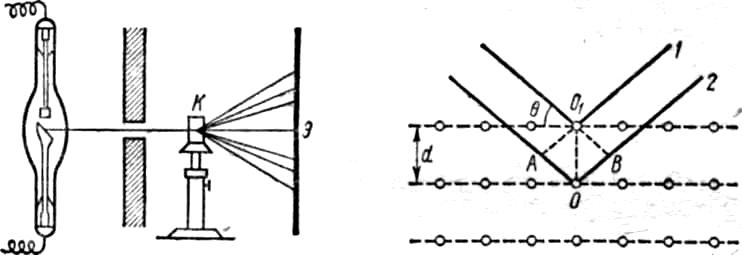
(б)

Монохроматичне рентгенівське випромінювання, потрапляючи на кристалічну решітку і дифрагуючи на ній, розсіюється. Промені, розсіяні від взаємно паралельних площин, віддалених одна від одної на відстанях, кратних міжплощинній відстані, є взаємно когерентними і, отже, можуть інтерферувати. Для визначення напрямів, по яких спостерігатимуться максимуми, треба знайти умову максимального посилення хвиль, які дифрагували від однієї вищезазначеної площин, і хвиль, що йдуть від сукупності взаємно паралельних площин. Із принципу Гюйгенса виходить, що взаємне посилення хвиль, розсіяних окремими центрами в межах однієї площини, відбудеться у випадку, якщо кут падіння дорівнює куту відбивання. Тільки в цьому випадку вони будуть поширюватися в одній фазі і, отже, накладаючись, взаємно підсилюватимуть один одного. Щоб відбулося посилення також хвиль, що йдуть від взаємно паралельних площин, різниця ходу між променями 1 і 2, відбитими від сусідніх площин (рис.2.43б), повинна дорівнювати цілому числу довжини хвилі. Якщо кут, доповнюючий кут падіння до 90°, позначити через (кут ковзання), то шукана різниця ходу буде . Отже, взаємне посилення відбудеться, якщо

2.38

де т = 1, 2, 3 ..., d — міжплощинна відстань.

При довільному напрямі падіння монохроматичного променя дифракція не виникає. В цьому випадку для спостереження дифракції необхідно, повертаючи кристал, знайти даний кут ковзання . Наприклад, якщо на кристал кальциту, міжплощинна відстань в якому дорівнює 3,029 Å, направити випромінювання з довжиною хвилі 1,54 Å, то дифракційний максимум першого порядку спостерігатиметься під кутом .

Формула (32) була виведена незалежно один від одного російським| кристалографом Ю. В. Вульфом і англійськими фізиками батьком|батьком| і сином Бреггами і тому носить назву формули Вульфа-Брегга.

За допомогою формули Вульфа-Брегга вирішують|рішають| два завдання|задачі|:

1. За відомою довжиною хвилі рентгенівського випромінювання, визначаючи і т, можна обчислити d, тобто знайти міжплощинну відстань, а відтак і постійну кристалічної решітки. Рішенням цієї задачі займається рентгеноструктурний аналіз.

2. За відомою кристалічною структурою (d), визначаючи і т, можна обчислити невідому довжину хвилі падаючого рентгенівського випромінювання. Цей напрям фізики називається рентгеноспектроскопією.