Роздільна здатність дифракційної решітки

Ч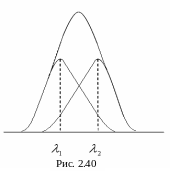 им більше постійна дифракційної решітки, тим більше спектрів можна спостерігати з|із| її допомогою, але|та| тим вони менш яскраві і вужчі, а отже менш придатні для спектрального аналізу. Можливість|спроможність| розділяти дві спектральні лінії, які мало відрізняються одна від одної за довжиною хвилі, тобто бачити їх у спектрі як дві лінії, а не як одну, визначається роздільною здатністю решітки.

Д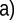 ля того, щоб спектральний апарат дав можливість|спроможність| установити наявність двох довжин хвиль (розділити дві довжини хвилі), необхідно, щоб при заданій відстані між максимумами їх контури були достатньо|досить| різкі.

Н а рис. 2.40 освітленості, що дає кожна лінія, змішуються. Ці дві лінії не розділені.

Рис. 2.41

На рис. 2.41 наявність двох максимумів (двох довжин хвиль) виступає|вирушати| достатньо|досить| виразно|чітко|, не зважаючи на те, що горби від кожної з них значною мірою|значною мірою| перекриваються. Ці лінії розділені.

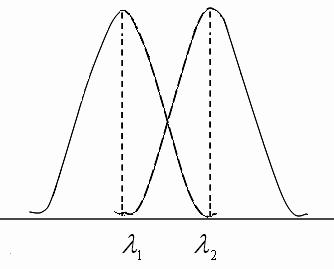З розуміло, що можливість|спроможність| розрізнення двох максимумів у цьому випадку залежить до певної міри від точності того методу, яким досліджується розподіл інтенсивності уздовж|вздовж,уподовж| спектру. Т аким чином, можливість|спроможність| розділення двох ліній є|з'являтися,являтися| невизначеною|неозначений|.

Рис. 2.42

За пропозицією Релея|речення| умовно прийнято вважати|лічити| розділення двох ліній
повним|цілковитий|, коли два горби розташовані|схильний| так, що максимум першого горба співпадає|збігатися| з найближчим|із| мінімумом другого (дивись рис.2.42).

Та найменша різниця в довжинах хвиль , яка задовольняє поставленій умові, і визначить собою здатність спектрального апарату відрізнити близькі довжини хвиль.

Якщо дві суміжні лінії мають однакову інтенсивність та форму, то критерій Релея|речення| означає, що мінімум між лініями складає близько 80% від сусідніх максимумів. Такий контраст встановлюється цілком|сповна| чітко.

За міру роздільної здатності спектрального апарату прийнято відношення|ставлення| довжини хвилі , біля якої виконується вимірювання|вимір|, до вказаного мінімального інтервалу , тобто

– роздільна здатність.

Умова Релея|речення| має вигляд:

;

; оскільки мале.

Оскільки|тому що| і близькі між собою, то

2.35 Роздільна здатність дорівнює добутку порядку|лад| спектру на число променів, що інтерферують у приладі.

Число пучків, що інтерферують, рівне числу щілин решітки.

В решітках велика роздільна здатність досягається тим, що велике , а далекі порядки спектрів накладаються.

Дисперсія дифракційних решіток

Основне призначення спектральних апаратів полягає у встановленні довжини хвилі досліджуваного світла – завдання|задача|, яке в більшості випадків зводиться до визначення відмінності в довжинах хвиль двох близьких спектральних ліній. Звичайне|звичний| положення|становище| спектральної лінії в апараті задається кутом|ріг,куток|, що визначає напрям|направлення| променів. Тому дисперсія визначається кутовою відстанню між лініями, що відрізняються за довжиною хвилі на 1 Å. Якщо двом лініям, що відрізняються за довжиною хвилі на , відповідає різниця кутів, рівна , то мірою дисперсії буде величина

– кутова дисперсія. 2.36

Оскільки|тому що| ми часто спостерігаємо положення|становище| лінії на екрані або фотопластині, то зручно замінити кутову відстань між лініями лінійною відстанню , вираженою|виказаною,висловленою|, наприклад, у міліметрах. Якщо фокусна відстань лінзи, що проектує спектр на екран, дорівнює , то, зрозуміло, , так що і виражається|виказується,висловлюється| в міліметрах на ангстрем. На практиці нерідко|незрідка| вказують|вказувати| обернену величину, характеризуючи дисперсію апарату числом ангстремів, що вкладається|вкладатися| на один міліметр фотопластини.

Нехай є дві близькі довжини хвилі і . Відстань між максимумами для і знайдеться|перебуде| з|із| умови, що визначає положення|становище| максимумів:

Диференціюючи, маємо:

. 2.37

Таким чином, дисперсія тим більша, чим менший період решітки і чим вищий порядок|лад| спостережуваного спектру.