3. Проектирование промежуточной диафрагмы

4. Статический расчет

Поперечные ребра диафрагмы рассматриваются как однопролетные свободно опертые балки. Нагрузка на них передается от плиты по закону треугольника (расстояния между диафрагмами больше ширины панели). Закон передачи нагрузки устанавливается путем проведения биссектрис углов между продольными и поперечными ребрами.

Схема загрузки диафрагмы (грузовая площадь):

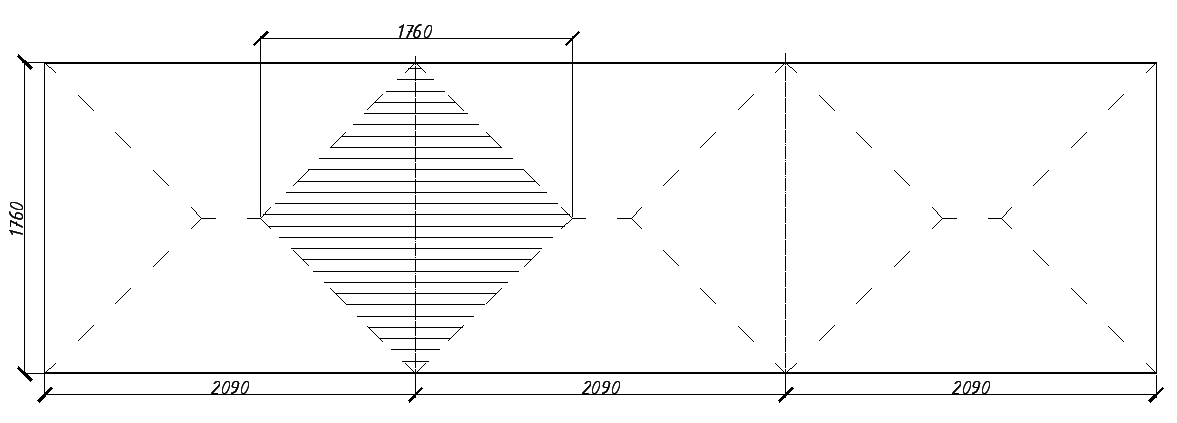
Рис 3.1

Величина расчетного пролета диафрагмы:

lд≈ b_пан ;

lд = 1520 мм.

Расчетная схема диафрагмы:

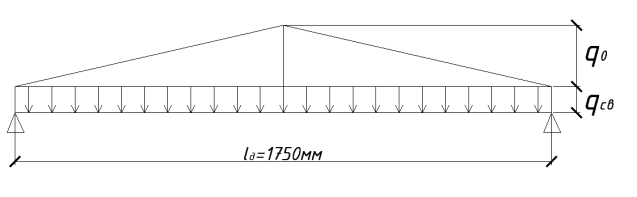
Рис 3.2

1. Нагрузка, действующая на один погонный метр диафрагмы:

q _св= (h_д – h_пл) · b_{д ср} · γ_ж/б · γ_f,

где b_{д ср} - средняя ширина сечения диафрагмы (b_{д ср} = 8 - 10см);

γ_ж/б - удельный вес железобетона (γ_ж/б = 2500 кгс/м³);

γ_f - коэффициент надежности по нагрузке (γ_f = 1,1).

Тогда q _св= (0,152– 0,06) · 0,08 · 2500 · 1,1=20 (кгс/м).

2) Наибольшее значение треугольной нагрузки q₀, передаваемой от плиты (включая вес плиты, вес пола и полезную нагрузку для средних диафрагм) найдем по формуле:

q_о= q_пл · b_пан;

Тогда q_о= 3180 · 1.52= 4834 (кгс/м).

3) Наибольший изгибающий момент в пролете и поперечная сила на опорах при треугольном законе передачи нагрузки определяется по формулам:

М_мах = q_св · l_д²/8 + q_о · l_д²/12,

Qmax = q_св · l_д/2 + q_о · l_д/4.

Тогда Мmax = 20 · 1.52²/8 + 4834 · 1.52²/12 =936 (кгс · м);

Qmax = 20 · 1.52/2 + 4834 · 1.52/4=1852 (кгс).

5. Расчет продольной арматуры

Диафрагма, изгибаясь под действием нагрузок сверху, вовлекает в работу прилегающие части плиты. Сечение становится не прямоугольным, а тавровым. Нейтральная линия, которая отличает сжатую зону от растянутой, может проходить в полке или в ребре.

Рис 3.3

1) Полезная высота диафрагмы:

h₀ = h_д- a,

где а = 2÷3 см.

Тогда h₀ = 0,152 - 0,02 = 0,132 (м).

2) Расчётная ширина полки, исходя из следующих критериев:

b_п  (1/3) lд ;

b_п  а_пан;

b_п  12h_п + b_{д ср}.

Подставляя найденные ранее значения, получаем:

b_п  (1/3) 1. 52  0.506м ;

b_п  2,03м;

b_п  12·0,06 + 0,08=0.8м.

Принимаем b_п=500мм

3) Положение нейтральной оси.

Предельный момент, воспринимаемый полкой:

M_n = b_n·h_n·R_b· (h₀-h_n/2);

Тогда M_n = 0,5·0,06·117·10⁴· (0,117-0,06/2) =3580 (кгс·м).

Так как Мmax = 936 кгс·м < М_п =3580 кгс·м, нейтральная ось проходит в полке и сечение рассчитывается как прямоугольное с шириной, равной ширине полки b_п.

4) Параметр Ао:

Ао=Мmax/(b_п·ho²·Rb);

Тогда Ао=936 ·100/(50·13.2²·117)= 0,092;

По таблице для найденного параметра А₀ определяем коэффициент η =0,95.

5) Площадь сечения продольной арматуры:

As= Мmax/(η ·ho·Rs);

Тогда As= 936 ·100/(0,95 ·13,2·3600) = 2.07 (см²).

Подбираем по сортаменту 8Ø6 А-III с As^факт=2,26 (см²).

6. Расчет поперечной арматуры

Диафрагма сборной панели армируется, как правило, одним плоским каркасом, который состоит из одного или двух рабочих стержней продольной арматуры, поперечных стержней – хомутов и одного монтажного стержня, диаметр которого назначается конструктивно:

d_{монтажного стержня} ≥ d_хомута +2мм.

Поперечная арматура (хомуты) ставится в балках для обеспечения их прочности по наклонным сечениям. Задача расчета поперечной арматуры состоит в подборе диаметра и шага хомутов.

1) Проверяем условие прочности по бетонной полосе между наклонными сечениями:

Qmax < 0,3·b·ho·Rb.

Тогда Qmax =1852 кгс < 0,3·8·13.2·117 = 3706 кгс

Условие выполняется.

2) Назначаем шаг хомутов, руководствуясь следующими ограничениями:

S  0,5 · h₀;

S  30 см;

S  b · ho² · R_bt/ Qmax.

Подставляя известные значения, получаем:

S  6.6 (см);

S  30 (см);

S  8 · 13.2² · 9,2/1852 =6,92 (см).

Принимаем S = 6.6 см.

3) Назначаем хомуты минимального диаметра Ø6 класса А-I.

Силу, сосредоточенную в хомутах, заменяем условно распределённой на единицу длины элемента силой q_sw:

q_sw= A_sw · R_sw/ S;

где A_sw – площадь поперечного сечения хомутов в одном поперечном сечении балки;

R_sw – расчетное сопротивление хомутов (R_sw=1750 кгс/см²).

Тогда q_sw= 0,283 · 1750/ 6.6=75 (кгс/см).

При этом должно выполняться следующее условие:

q_sw ≥ 0,25 · R_bt · b;

q_sw ≥ 0,25 · 9,2 · 8=18.4кгс/см;

Условие выполняется. Принимаем q_sw = 75кгс/см.

4) Определяем момент Mb:

Мb=1,5 · b · ho² · R_bt;

Тогда, Мв=1,5 · 8 · 13.2² · 9,2=19236 (кгс · см).

5) Проверяем выполнение условия, при котором предельная поперечная сила на опоре, воспринимаемая диафрагмой, должна быть больше поперечной силы в нормальном сечении элемента: .

;

Полагаем в запас прочности, что q=0, так как нагрузка не является равномерно распределённой. Подставляя ранее найденные значения, получаем:

=2080 (кгс) ≥ 1852 (кгс).

Условие выполняется. Тогда проверяем следующее условие:

=1762,4 (кгс) 1852 (кгс).

Условие не выполняется. Значит увеличивает диаметр хомута. Назначаем хомуты диаметром Ø7.

Тогда q_sw= 0,385 · 1750/ 6.6=102,1 (кгс/см);

q_sw ≥ 0,25 · 9,2 · 8=18.4кгс/см;

Условие выполняется. Принимаем q_sw = 102,1 кгс/см.

Мb=1,5 · 8 · 13.2² · 9,2=19236 (кгс · см).

=2427 (кгс) ≥ 1852 (кгс).

Условие выполняется.

=2299 (кгс) ≥ 1852 (кгс).

Условие выполняется.

6) Значение длины проекции наклонного сечения С:

;

(кгс) ≥ 1852 (кгс).

Так как , то окончательно принимаем хомуты Ø7 А-I с шагом S = 6.6 см.

Принимаем диаметр монтажного стержня равным 9 мм.

Рис 3.4