1. Установить взаимосвязи между исходными и выходными показателями в виде математического уравнения или неравенства.

2. Задать законы распределения вероятностей для ключевых параметров модели. Основные законы распределения непрерывных случайных величин Равномерный закон распределения.

СВ X распределена по рав­номерному (прямоугольному) закону, если все значения СВ лежат внутри некоторого интервала и все они равновероятны (точнее, обла­дают одной плотностью вероятности). Например, если весы имеют точность 1г и полученное значение округляется до ближайшего цело­го числа к, то точный вес можно считать равномерно распределенной СВ на интервале (t-0,5; к+0,5).

Дифференциальная функция равномерного закона на интервале (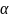 , ) (рис.11):

f(x) =

Интегральная функция равномерного закона на интервале (

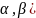
F(x) =

F( )

1

Дифференциальная функция Интегральная функция

Рис. Равномерный закон распределения

1. Математическое ожидание:

M(X) .

М(Х) совпадает, в силу симметрии распределения, с медианой.

2. Моды равномерное распределение не имеет.

3. Дисперсия D(X) = =

4. Вероятность попадания св в заданный интервал (

.

Показательное распределение. НСВ X, принимающая неотрица­тельные значения, имеет показательное распределение, если ее диф­ференциальная функция имеет вид:

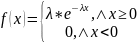
Интегральная функция показательного закона

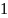
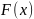
Дифференциальная функция Интегральная функция

Рис. Показательный закон распределения

Нормальный закон распределения (рис. 14) играет исключи­тельную роль в теории вероятностей. Это наиболее часто встречаю­щийся закон распределения, главной особенностью которого — то, что он является предельным законом, к которому, при определенных ус­ловиях, приближаются другие законы распределения.

Дифференциальная функция нормального закона имеет вид:

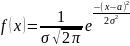
M(X)=a – характеризует центр распределения

D(X)=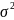 – характеризует форму распределения

Вероятность попадания нормальной случайной величины в заданный интервал определяется по свойству интегральной функции:

P(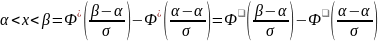

где 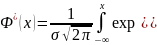- интегральная функция нормального закона, Ф(x) – функция Лапласа

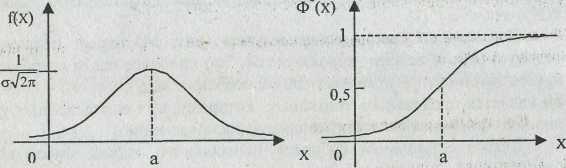
Дифференциальная функция Интегральная функция

Рис. Нормальный закон распределения

3. Провести компьютерную имитацию значений ключевых параметров модели.

4. Рассчитать основные характеристики распределений исходных и выходных показателей.

5. Провести анализ полученных результатов и принять решение.

Результаты имитационного эксперимента могут быть дополнены статистическим анализом, а также использоваться для построения прогнозных моделей и сценариев.

Применение метода Монте-Карло может дать существенный эффект при моделировании развития процессов, натурное наблюдение которых нежелательно или невозможно, а другие математические методы применительно к этим процессам либо не разработаны, либо неприемлемы из-за многочисленных оговорок и допущений, которые могут привести к серьезным погрешностям или неправильным выводам. В связи с этим необходимо не только наблюдать развитие процесса в нежелательных направлениях, но и оценивать гипотезы о параметрах нежелательных ситуаций, к которым приведет такое развитие, в том числе и параметрах рисков.

Существуют различные методы проверки статистических гипотез.

Наиболее широко используются на практике критерии:

• согласия ² (хи-квадрат);

• Крамера-фон Мизеса;

• Колмогорова-Смирнова

19