10.2. Нелинейное преобразование гармонического колебания

Предложим, что на вход нелинейной РТЦ действует гармоническое колебание частоты , а на выходе появляется качественно новое колебание другой частоты. Выясним:

1) каковы закономерности процесса нелинейного преобразования и его возможные результаты?

2) каковы способы оптимального использования этих результатов и области их применения?

В этом параграфе попытаемся ответить на первый вопрос, а в последующих − на второй. J

Процесс преобразования. Рассмотрим его применительно к функциональной схеме рис. 10.2, а На вход нелинейного элемента подано напряжение смещения , определяющее положение ТИР на нелинейном участке ВАХ, и гармоническое напряжение 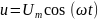, охватывающее значительную часть этого участка и выходящее за пределы ВАХ.

Как видно из графика, положению ТИР в исходном режиме соответствует ток покоя , а в рабочем − нелинейном режиме − импульсы тока несинусоидальной формы, частоты . Как любую периодическую функцию, эти импульсы можно разложить в ряд Фурье на постоянную составляющую и совокупность гармоник: 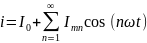. Любая из составляющих этого спектра может быть выделена при помощи фильтра в виде напряжения .

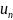При выпрямлении используется постоянная составляющая для выделения которой надо применять сглаживающий фильтр − ФНЧ, не пропускающий гармоник.

При амплитудном детектировании входное напряжение представляет собой АМС. В результате его преобразования в спектре тока возникает составляющая частоты модуляции, которую выделяет ФНЧ.

При нелинейном усилении используется ПФ, настроенный на частоту первой гармоники и активной НЭ, обладающий усилительными свойствами.

При умножении частоты ПФ настраивают на частоту одной из высших гармоник , при удвоении частоты на вторую гармонику, а при утроении − на третью.

Итак, любое из названных применений нелинейной РТЦ является следствием единого процесса − нелинейного преобразования гармонического колебания, который состоит из двух операций: искажения колебания НЭ, в результате которого в спектре возникает требуемая составляющая, и фильтрации этой составляющей.

Гармонический анализ. Данный анализ проводится для определения значений составляющих 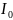и 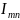и зависит от свойств НЭ и его режима. Результаты анализа дают возможность рассчитать и отрегулировать оптимальный режим НЭ. Процесс анализа можно разделить на следующие этапы.

1) аппроксимация ВАХ − замена реальной ВАХ идеализированной, которую можно описать относительно простым уравнением

2. математические преобразования, в ходе которых в уравнение аппроксимирующее ВАХ, подставляют модель сигнала (в нашем случае , а затем полученное выражение 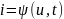преобразует так, чтобы получить формулу ряда Фурье с коэффициентами и выраженными через напряжения , и параметры НЭ;

3. табулирование. Результаты анализа желательно представить в виде таблиц или графиков, которые могут быть легко использованы для расчета составляющих при решении широкого круга задач.

Аппроксимация ВАХ. Аппроксимирующие уравнения различны в зависимости от формы ВАХ. Ограничимся широко используемой аппроксимацией ВАХ степенным многочленом

.

Если, например, НЭ − триод, то − ток коллектора (анода, стока), − ток покоя при 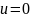, − напряжение между базой и эмиттером (сеткой и катодом, затвором и истоком), 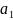− крутизна проходной ВАХ и ТИР ( ). Если известны коэффициенты 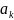то, подставляя в значения и вычисляя , можно построить аппроксимирующую ВАХ.

Кусочно-линейная аппроксимация. Если в уравнении (10.2) ограничиться первыми двумя слагаемыми, получим уравнение прямой:

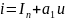
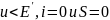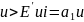которая, как видно из рис. 10.2, б, хорошо совпадает с ВАХ на ее линейном участке (утолщенный отрезок). Идеализированная ВАХ состоит из отрезков (кусков) прямой. На горизонтальном участке тока нет: . На восходящем . Крутизна ВАХ постоянна: .

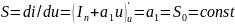Точке излома ВАХ соответствует напряжение 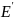называемое напряжением отсечки, сдвига или геометрического смещения, и началу восходящего участка идеализированной ВАХ по отношению к началу координат – (параметр НЭ).

На рис. 10.2, б показана так называемая "правая" ВАХ. Для нее 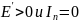. Для "левых" ВАХ 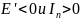(рис. 10.2, в).

Кусочно-линейная аппроксимация находит широкое применение при больших амплитудах , при которых в основном используются линейные участки ВАХ.

Аппроксимация квадратичной параболой. Такая аппроксимация оказывается достаточно точной для ВАХ многих НЭ, если амплитуда не выходит за пределы нижнего сгиба ВАХ − утолщенный участок на рис. 10.2, б. В этом случае 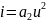. Крутизна ВАХ на этом участке линейно возрастает. Действительно,

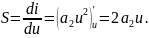
Следовательно, − угловой коэффициент прямой, по которой изменяется крутизна*.

Рассмотрим важные для дальнейшего результаты гармонического анализа.

Анализ при кусочно-линейной ВАХ. Этот анализ впервые провел А. И. Берг. На рис. 10.2, в показана "левая" ВАХ. В исходном режиме НЭ закрыт, так как ТИР левее линии отсечки 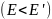. Положительная полуволна напряжения (напряжения возбуждения) открывает НЭ на время , в течение которого формируется косинусоидальный импульс тока Его максимальное значен ие − "высота" импульса – 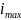_> а длительность принято оценивать углом отсечки.

Угол отсечки 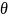− это фазовый угол 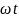, соответствующий половине импульса. При

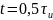
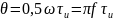
Эту формулу удобно использовать для отсчета угла по осциллограмме тока . Для этого надо подставить в (10.5) пропорциональное и число делений масштабной сетки (рис, 10.2, в).

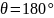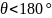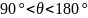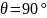В линейном режиме отсечки нет ( ) и его называют также режимом колебаний / рода или режимом класса А. В нелинейном режиме и его называют режимом колебаний II рода. В зависимости от значения различают режимы классов: АВ ( ), В ( ) и С ( ).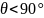

Коэффициенты ра:ыожения. Составляющие последовательности косинусоидальных импульсов зависят от их параметров: 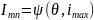. Для того чтобы исключить зависимость от значения которого произвольны, используются относительные значения составляющих, называемые коэффициентами разложения косинусоидальных импульсов:

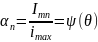
Коэффициенты постоянной составляющей и гармоник: 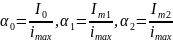и т.д., зависят от так как при любом его изменении во столько же раз меняется , а их отношение 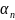неизменно.

Графики функций А. И. Берга. Названные графики (рис. 10.2, в) построены по результатам расчетов, сведенным в таблицы. Расчетные формулы − это выражения для 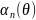, полученные путем разложения косинусоидальной функции в ряд Фурье. Значения а_л получены путем подстановки в эти формулы значений от до .

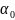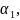
Расчет составляющих. Заданы и . По графикам А. И. Берга для заданного находят , , 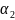,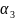..., а затем вычисляют

Пример: Определить составляющие если для биполярного транзистора известны 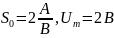, а на осциллограмме наблюдаются одно-полупериодггые импульсы: .

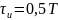1. Угол отсечки .

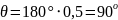2- Высота импульса

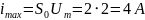
3. Коэффициенты разложения (по графику): .

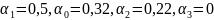4. Значения составляющих:

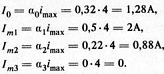
Анализ при квадратичной ВАХ. Пусть даны уравнение ВАХ

(10.8)

и модель сигнала (рис. 10.2, г). Произведем подстановку в (10.8) 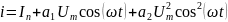. Учитывая, что 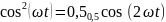, получаем выражение для частотного спектра тока

Спектр состоит из постоянной составляющей, первой и второй гармоник. Постоянная составляющая 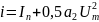содержит два слагаемых: (ток покоя в исходном режиме) и 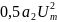которое пропорционально квадрату амплитуды и возникает в результате так называемого детекторного эффекта − возрастания среднего значения тока за счет такого искажения его формы, при котором положительные приращения к току больше отрицательных (см. графики на рис. 10.2, а). Первая гармоника формируется за счет линейного (первой степени) слагаемого (10.9). 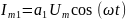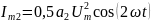Вторая гармоника формируется за счет квадратичного (второй степени) слагаемого (10.9).

Отмеченные закономерности позволяют сделать следующие выводы, справедливые для многочлена любой степени :

1. Нечетные гармоники формируются за счет слагаемых аппроксимирующего уравнения (10.2) нечетных степеней, постоянная составляющая и четные гармоники − за счет четных.

2. Номер гармоники не выше показателя степени .

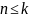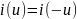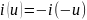Из этих выводов вытекает правило (рис. 10.2,г). Если ВАХ − четная функция относительно ТИР, т. е. если и график симметричен относительно вертикальной оси, то при симметричном изменении спектр тока может содержать только постоянную составляющую и четные гармоники. Если функция нечетная , то спектр тока содержит только нечетные гармоники. Это правило можно использовать при анализе или синтезе схем, рассчитанных на выделение заданных составляющих спектра.