
1 Гидрологические расчеты
Целью гидрологических расчетов является определение гарантированного водосъемного уровня, продолжительности вывода полотов и отметки заложения дна плотбища.
Под гарантированным съемным уровнем понимают минимальный уровень весеннего половодья, который обеспечивается с вероятностью
95% в течение заданного периода вывода плотов с плотбища.
Гарантированный съемный уровень определяют в результате статистической обработки многолетних водомерных наблюдений по опорному водомерному посту.
1.1 РАСЧЕТ ЭМПИРИЧЕСКОЙ КРИВОЙ, ГАРАНТИРОВАННЫХ УРОВНЕЙ ЗА 6,9,12 И 15 ДНЕЙ ПОСЛЕ ЛЕДОХОДА
Из [1(табл.1,прил.3)], устанавливаем для каждого года минимальные уровни весеннего половодья по опорному водомерному посту Hоп. Данные заносим в таблицу 1.
Используя данные из [1(табл.2,прил.4)], строим график связи уровней опорного водомерного поста Hоп и водомерного поста на плотбище H, рисунок 1
По графику связи уровней при известных уровнях для опорного поста Hоп определяют соответственные уровни для водомерного поста на плотбище H. Результаты заносят в таблицу 1.
Таблица 1.Исходные данные для построения кривой связи уровней опорного водомерного поста Ноп и водомерного поста на плотбище Н
Параметр |
Номер точки |
||||
1 |
2 |
3 |
4 |
5 |
|
Ноп, см |
150 |
250 |
350 |
450 |
550 |
Н, см |
205 |
280 |
355 |
450 |
470 |
Рисунок 1.Кривая связи.
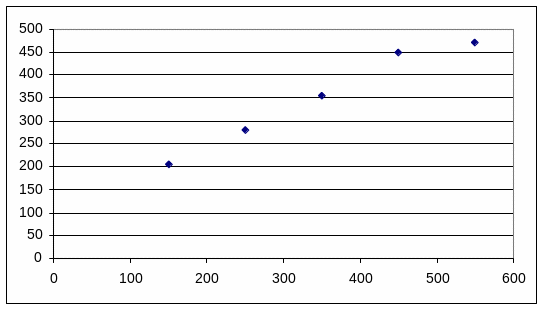

Соответственные уровни располагают в убывающем порядке, в графе Hi .
Модульный коэффициент вычисляем по формуле:
![]() (1.1)
(1.1)
где Hi- i-е значение уровня убывающего ряда, для 1-го значения;
Hi=429см;
Hср- среднее арифметическое значение ряда уровней
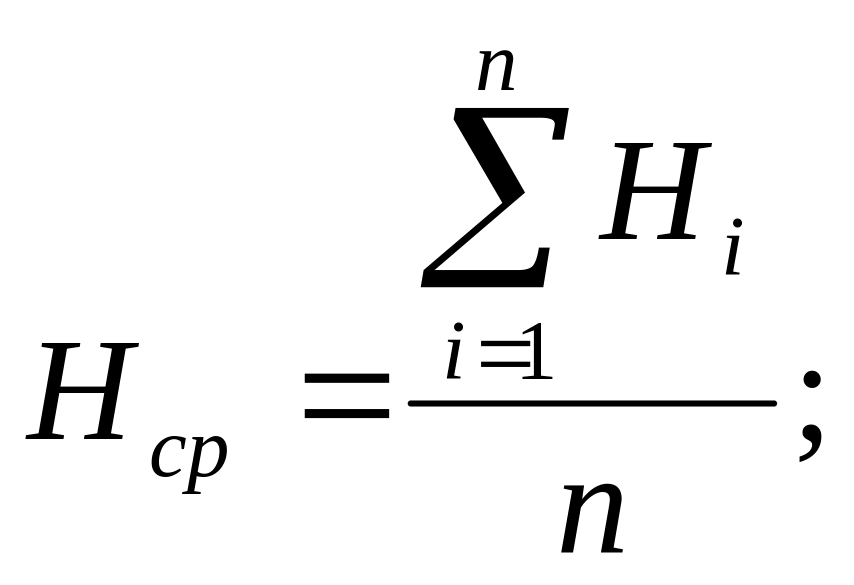 (1.2)
(1.2)
где n – количество членов в ряду n=20;
![]()
Например модульный коэффициент для первого значения из ряда Hi
![]()
Обеспеченность,%, вычисляем по формуле:
![]() (1.3)
(1.3)
где m- порядковый номер уровня в убывающем ряду;
n- число лет наблюдений n=20;
Например: обеспеченность для первого значения убывающего ряда Hi,
Будет
равна:
![]()
![]()
Результаты расчетов сводим в таблицу 1
Таблица 2-Расчет эмпирической кривой, гарантированных уровней за
дней после ледохода
Год |
Ноп,см |
Н,см |
m |
Нi,см |
Ki |
(Ki-1) |
(Ki-1)2 |
P,% |
1983 |
345 |
342 |
1 |
429 |
1,2839 |
0,2839 |
0,0805992 |
5 |
1984 |
385 |
370 |
2 |
412 |
1,233 |
0,233 |
0,054289 |
10 |
1985 |
445 |
412 |
3 |
380 |
1,1372 |
0,1372 |
0,0188238 |
14 |
1986 |
470 |
429 |
4 |
377 |
1,1282 |
0,1282 |
0,0164352 |
19 |
1987 |
315 |
321 |
5 |
370 |
1,1073 |
0,1073 |
0,0115133 |
24 |
1988 |
270 |
289 |
6 |
366 |
1,0953 |
0,0953 |
0,0090821 |
29 |
1989 |
350 |
345 |
7 |
363 |
1,0863 |
0,0863 |
0,0074477 |
33 |
1990 |
395 |
377 |
8 |
356 |
1,0654 |
0,0654 |
0,0042772 |
38 |
1991 |
345 |
342 |
9 |
345 |
1,0325 |
0,0325 |
0,0010563 |
43 |
1992 |
365 |
356 |
10 |
342 |
1,0235 |
0,0235 |
0,0005523 |
48 |
1993 |
400 |
380 |
11 |
342 |
1,0235 |
0,0235 |
0,0005523 |
52 |
1994 |
315 |
321 |
12 |
321 |
0,9606 |
-0,039 |
0,0015524 |
57 |
1995 |
195 |
237 |
13 |
321 |
0,9606 |
-0,039 |
0,0015524 |
62 |
1996 |
225 |
258 |
14 |
310 |
0,9277 |
-0,072 |
0,0052273 |
67 |
1997 |
375 |
363 |
15 |
300 |
0,8978 |
-0,102 |
0,0104448 |
71 |
1998 |
245 |
272 |
16 |
293 |
0,8769 |
-0,123 |
0,0151536 |
76 |
1999 |
285 |
300 |
17 |
289 |
0,8649 |
-0,135 |
0,018252 |
81 |
2000 |
380 |
366 |
18 |
272 |
0,814 |
-0,186 |
0,034596 |
86 |
2001 |
300 |
310 |
19 |
258 |
0,7721 |
-0,228 |
0,0519384 |
90 |
2002 |
275 |
293 |
20 |
237 |
0,7093 |
-0,291 |
0,0845065 |
95 |
итого |
|
|
|
6683 |
20 |
0 |
0,4278516 |
|
Определяем коэффициент вариации по формуле:
![]() (1.4)
(1.4)
![]()
Коэффициент асимметрии принимаем Cs=2Cv; (1.5)
Сs=2∙0,1501=0,3002
Правильность расчетов в таблице проверяем по формулам:
![]()
![]() условие
выполняется;
условие
выполняется;
![]()
![]() условие
выполняется;
условие
выполняется;
Таблица 3-Расчет эмпирической кривой обеспеченности уровней, гарантированных за 9 дней после ледохода
Год |
Ноп,см |
Н,см |
m |
Нi,см |
Ki |
(Ki-1) |
(Ki-1)2 |
P,% |
1983 |
325 |
328 |
1 |
398 |
1,2783 |
0,2783 |
0,0774509 |
5 |
1984 |
345 |
342 |
2 |
384 |
1,2331 |
0,2331 |
0,0543356 |
10 |
1985 |
405 |
384 |
3 |
356 |
1,1432 |
0,1432 |
0,0205062 |
14 |
1986 |
425 |
398 |
4 |
349 |
1,1207 |
0,1207 |
0,0145685 |
19 |
1987 |
280 |
296 |
5 |
345 |
1,1079 |
0,1079 |
0,0116424 |
24 |
1988 |
240 |
268 |
6 |
342 |
1,0983 |
0,0983 |
0,0096629 |
29 |
1989 |
325 |
328 |
7 |
342 |
1,0983 |
0,0983 |
0,0096629 |
33 |
1990 |
365 |
356 |
8 |
328 |
1,0533 |
0,0533 |
0,0028409 |
38 |
1991 |
315 |
321 |
9 |
328 |
1,0533 |
0,0533 |
0,0028409 |
43 |
1992 |
315 |
321 |
10 |
321 |
1,0308 |
0,0308 |
0,0009486 |
48 |
1993 |
350 |
345 |
11 |
321 |
1,0308 |
0,0308 |
0,0009486 |
52 |
1994 |
275 |
293 |
12 |
296 |
0,9505 |
-0,05 |
0,0024503 |
57 |
1995 |
175 |
223 |
13 |
293 |
0,9409 |
-0,059 |
0,0034928 |
62 |
1996 |
205 |
244 |
14 |
289 |
0,9281 |
-0,072 |
0,0051696 |
67 |
1997 |
345 |
342 |
15 |
275 |
0,8831 |
-0,117 |
0,0136656 |
71 |
1998 |
215 |
251 |
16 |
275 |
0,8831 |
-0,117 |
0,0136656 |
76 |
1999 |
250 |
275 |
17 |
268 |
0,8606 |
-0,139 |
0,0194324 |
81 |
2000 |
355 |
349 |
18 |
251 |
0,806 |
-0,194 |
0,037636 |
86 |
2001 |
270 |
289 |
19 |
244 |
0,7836 |
-0,216 |
0,046829 |
90 |
2002 |
250 |
275 |
20 |
223 |
0,7161 |
-0,284 |
0,0805992 |
95 |
итого |
|
|
|
6228 |
20 |
0 |
0,4283489 |
|
![]()
Определяем коэффициент вариации по формуле (1.4)
![]()
Коэффициент ассиметрии по формуле (1.5)
Сs=2∙0,1501=0,3002
Правильность расчетов проверяем по условиям:
![]()
![]() -
условие выполняется;
-
условие выполняется;
- условие выполняется.
Таблица 4-Расчет эмпирической кривой, гарантированных уровней
за 12 дней после ледохода
Год |
Ноп,см |
Н,см |
m |
Нi,см |
Ki |
(Ki-1) |
(Ki-1)2 |
P,% |
1983 |
290 |
303 |
1 |
373 |
1,2678 |
0,2678 |
0,0717168 |
5 |
1984 |
320 |
324 |
2 |
363 |
1,2343 |
0,2343 |
0,0548965 |
10 |
1985 |
375 |
363 |
3 |
335 |
1,1391 |
0,1391 |
0,0193488 |
14 |
1986 |
390 |
373 |
4 |
331 |
1,1255 |
0,1255 |
0,0157503 |
19 |
1987 |
245 |
272 |
5 |
331 |
1,1255 |
0,1255 |
0,0157503 |
24 |
1988 |
220 |
254 |
6 |
328 |
1,1153 |
0,1153 |
0,0132941 |
29 |
1989 |
295 |
307 |
7 |
324 |
1,1017 |
0,1017 |
0,0103429 |
33 |
1990 |
330 |
331 |
8 |
307 |
1,0439 |
0,0439 |
0,0019272 |
38 |
1991 |
285 |
300 |
9 |
307 |
1,0439 |
0,0439 |
0,0019272 |
43 |
1992 |
295 |
307 |
10 |
303 |
1,0303 |
0,0303 |
0,0009181 |
48 |
1993 |
335 |
335 |
11 |
300 |
1,0201 |
0,0201 |
0,000404 |
52 |
1994 |
245 |
272 |
12 |
279 |
0,9487 |
-0,051 |
0,0026317 |
57 |
1995 |
160 |
212 |
13 |
272 |
0,9249 |
-0,075 |
0,00564 |
62 |
1996 |
185 |
230 |
14 |
272 |
0,9249 |
-0,075 |
0,00564 |
67 |
1997 |
325 |
328 |
15 |
270 |
0,9181 |
-0,082 |
0,0067076 |
71 |
1998 |
195 |
237 |
16 |
254 |
0,8637 |
-0,136 |
0,0185777 |
76 |
1999 |
220 |
254 |
17 |
254 |
0,8637 |
-0,136 |
0,0185777 |
81 |
2000 |
330 |
331 |
18 |
237 |
0,8058 |
-0,194 |
0,0377136 |
86 |
2001 |
255 |
279 |
19 |
230 |
0,782 |
-0,218 |
0,047524 |
90 |
2002 |
243 |
270 |
20 |
212 |
0,7208 |
-0,279 |
0,0779526 |
95 |
итого |
|
|
|
5882 |
20 |
0 |
0,4272411 |
|
![]()
Определяем коэффициент вариации:
![]()
Коэффициент ассиметрии:
Сs=2∙0,15=0,3;
Проверяем правильность расчетов:
- условие выполняется;
- условие выполняется;
Таблица 5-Расчет эмпирической кривой, гарантированных уровней
за 15 дней после ледохода
Год |
Ноп,см |
Н,см |
m |
Нi,см |
Ki |
(Ki-1) |
(Ki-1)2 |
P,% |
1983 |
265 |
286 |
1 |
328 |
1,1839 |
0,1839 |
0,0338192 |
5 |
1984 |
290 |
303 |
2 |
328 |
1,1841 |
0,1841 |
0,0338928 |
10 |
1985 |
325 |
328 |
3 |
324 |
1,1697 |
0,1697 |
0,0287981 |
14 |
1986 |
325 |
328 |
4 |
317 |
1,1444 |
0,1444 |
0,0208514 |
19 |
1987 |
220 |
254 |
5 |
314 |
1,1336 |
0,1336 |
0,017849 |
24 |
1988 |
200 |
240 |
6 |
310 |
1,1191 |
0,1191 |
0,0141848 |
29 |
1989 |
280 |
296 |
7 |
303 |
1,0939 |
0,0939 |
0,0088172 |
33 |
1990 |
310 |
317 |
8 |
296 |
1,0686 |
0,0686 |
0,004706 |
38 |
1991 |
255 |
279 |
9 |
286 |
1,0325 |
0,0325 |
0,0010563 |
43 |
1992 |
260 |
282 |
10 |
282 |
1,0181 |
0,0181 |
0,0003276 |
48 |
1993 |
305 |
314 |
11 |
279 |
1,0072 |
0,0072 |
5,184E-05 |
52 |
1994 |
220 |
254 |
12 |
265 |
0,9567 |
-0,043 |
0,0018749 |
57 |
1995 |
145 |
202 |
13 |
265 |
0,9567 |
-0,043 |
0,0018749 |
62 |
1996 |
165 |
216 |
14 |
254 |
0,917 |
-0,083 |
0,006889 |
67 |
1997 |
300 |
310 |
15 |
254 |
0,917 |
-0,083 |
0,006889 |
71 |
1998 |
190 |
233 |
16 |
244 |
0,8809 |
-0,119 |
0,0141848 |
76 |
1999 |
205 |
244 |
17 |
240 |
0,8664 |
-0,134 |
0,017849 |
81 |
2000 |
320 |
324 |
18 |
233 |
0,8412 |
-0,159 |
0,0252174 |
86 |
2001 |
235 |
265 |
19 |
216 |
0,7798 |
-0,22 |
0,048488 |
90 |
2002 |
235 |
265 |
20 |
202 |
0,7292 |
-0,271 |
0,0733326 |
95 |
итого |
|
|
|
5540 |
20 |
0 |
0,3609538 |
|
![]()
Определяем коэффициент вариации:
![]()
Коэффициент ассиметрии:
Сs=2∙0,1378=0,2756;
Проверяем правильность расчетов:
- условие выполняется;
- условие выполняется;
По рассчитанным значениям и соответствующим уровням Нi строим эмпирическую кривую обеспеченности в виде ломанных линий.
Из таблицы 3 [2,прил 3] при Cv =0,1501определяем интерполяцией модульные коэффициенты кр при (Р=1...99%);
Кр1%=1,385
Вычисляем уровни разного процента обеспеченности:
Нр=кр∙Нср (1.6)
Нр=1,385∙334,15=463 (см)
Результаты расчетов сводим в таблицу 6, а затем на основании этой таблицы строим теоретические кривые обеспеченности в виде плавных кривых: Рисунок 2, Рисунок 3, Рисунок 4, Рисунок 5.
По теоретической кривой обеспеченности определяют минимальный съемный уровень маловодного года 95% обеспеченности.
Строим график зависимости съемных уровней от продолжительности их стояния, Рисунок 6, съемные уровни Нi берем из таблицы 5 по 95%-ой обеспеченности.
Предельная продолжительность вывода плотов – 13 суток (по заданию).
Теоретическая кривая должна совпадать с эмпирической кривой или проходить вблизи эмпирических точек.
Задавшись предельной продолжительностью вывода плотов t (приложение 4, таблица 1) по рисунку 4 устанавливаем расчетное значение гарантированного съемного уровня Hс.у . Отметку заложения дна плотбища (в системе водомерного поста на плотбище ) рассчитываем по формуле:
Hпл = 0+Hс.у-(Т+ Z),
где
отметка нуля графика водомерного поста на плотбище (приложение 4, таблица 1);
Т- максимальная осадка пучков (приложение 4, таблица 1);
Z- донный запас, принимаемый для плотбища равным 0,3м.
Чтобы не допустить примерзания пучков к грунту отметка плотбища Hпл не должна быть ниже отметки уровня ледостава Hл 5% -ной обеспеченности для плотбищ 1 категории.
Hпл=29,8+2,23-(1,2+0.3) =30,53 (м)
Отметку ледостава рассчитаем по формуле:
Hл=0+Hл,
где Hл-уровень ледостава 5%-ой обеспеченности (приложение 3, таблица 5);
Hл=29,8+0,3=30,1 (м)
Так как Hпл>Hл, мы не уменьшаем предельную продолжительность вывода плотов и принимаем t=13 суток.
Показатель |
Обеспеченность, Р,% |
||||||||||||
1 |
5 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
95 |
99 |
|
Через 6 дней после ледохода Сv=0,1501 |
|||||||||||||
Кр |
1,385 |
1,26 |
1,195 |
1,12 |
1,07 |
1,03 |
0,991 |
0,978 |
0,905 |
0,872 |
0,814 |
0,769 |
0,688 |
Нр,см |
463 |
421 |
399 |
374 |
358 |
344 |
331 |
327 |
302 |
291 |
272 |
257 |
230 |
Через 9 дней после ледохода Cv=0,1501 |
|||||||||||||
Кр |
1,385 |
1,26 |
1,195 |
1,12 |
1,07 |
1,03 |
0,991 |
0,978 |
0,905 |
0,872 |
0,814 |
0,769 |
0,688 |
Нр,см |
431 |
392 |
372 |
349 |
333 |
321 |
309 |
305 |
282 |
272 |
253 |
239 |
214 |
Через 12 дней после ледохода Сv=0,1501 |
|||||||||||||
Кр |
1,385 |
1,26 |
1,195 |
1,12 |
1,07 |
1,03 |
0,991 |
0,978 |
0,905 |
0,872 |
0,814 |
0,769 |
0,688 |
Нр,см |
407 |
371 |
351 |
329 |
315 |
303 |
291 |
288 |
266 |
257 |
239 |
226 |
202 |
Через 15 дней после ледохода Сv=0,1378 |
|||||||||||||
Кр |
1,352 |
1,238 |
1,179 |
1,11 |
1,065 |
1,028 |
0,993 |
0,959 |
0,923 |
0,883 |
0,829 |
0,787 |
0,711 |
Нр,см |
375 |
343 |
327 |
308 |
295 |
285 |
275 |
266 |
256 |
245 |
230 |
217 |
196 |
Таблица 6 - Данные для построения теоретической кривой

Рисунок 2. Теоретическая и эмпирическая кривые обеспеченности
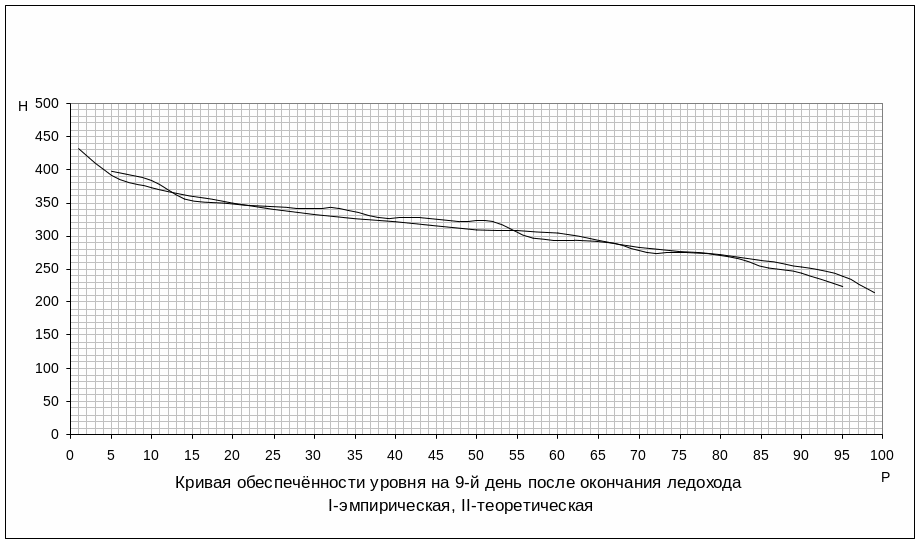
Рисунок 3. Теоретическая и эмпирическая кривые обеспеченности
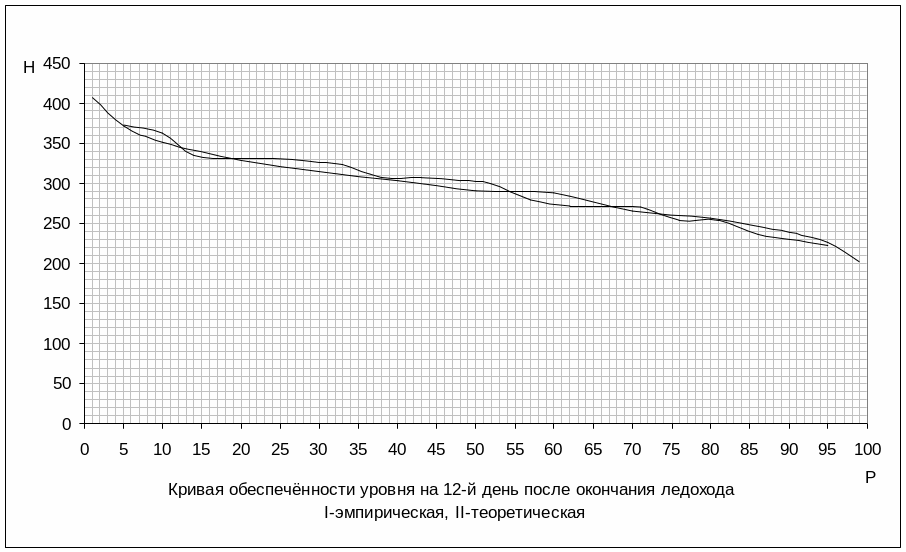
Рисунок 4. Теоретическая и эмпирическая кривые обеспеченности
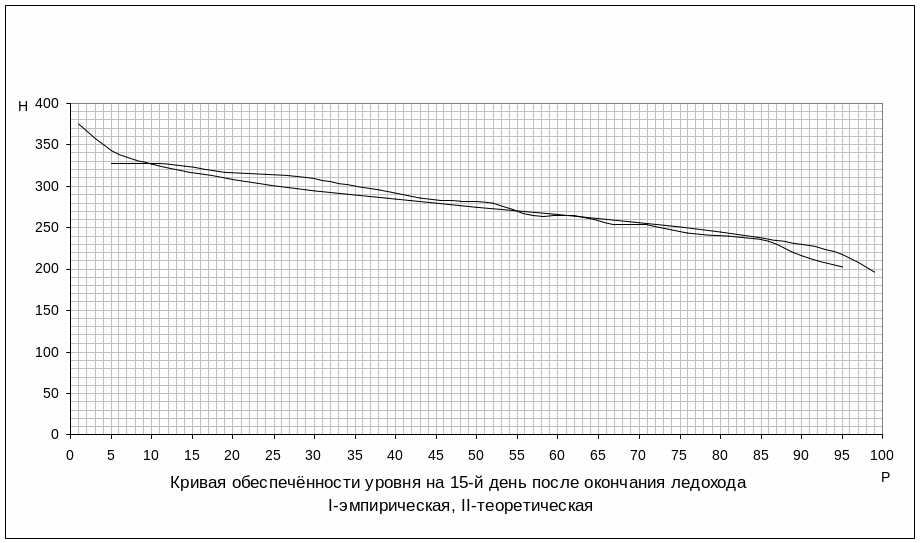
Рисунок 5. Теоретическая и эмпирическая кривые обеспеченности
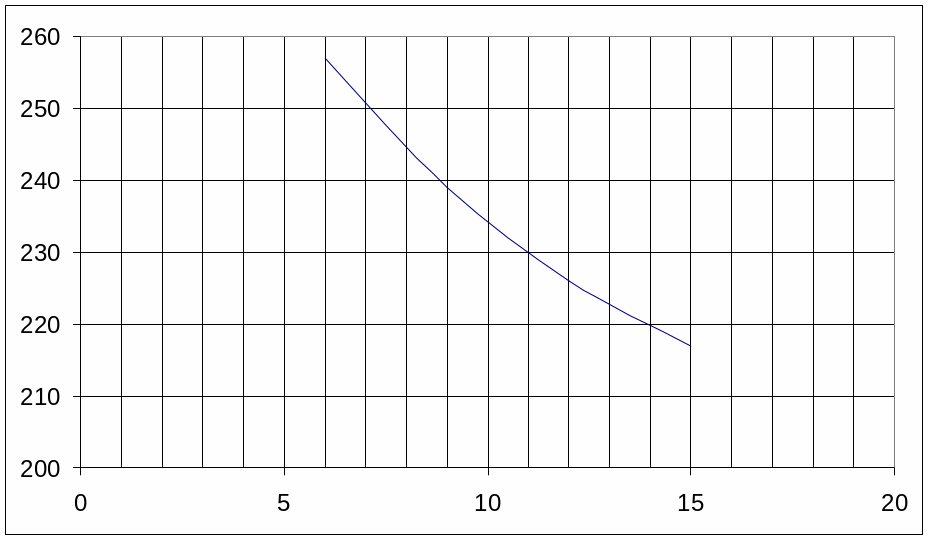
Рисунок 6. График зависимости съемных уровней от продолжительности их стояния
