1. Механическая система, как система материальных точек.

Системой материальных точек или механической системы, называют систему взаимных между собой материальных точек. Твёрдое тело в механике рассматривается как совокупность материальных точек. Различают свободные и несвободные системы. Свободной, называется система точек, которые могут получить произвольное перемещение и скорости, в противном случае несвободная система.

2. Внутренние и внешние силы.

С одной стороны силы, действующие на систему, различаются на активные и пассивные, другой стороны – внешние и внутренние.

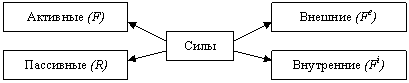
(Суммарными характеристиками меры механического движения является: 1) количество движения системы, 2) момент количества движения, 3) кинетическая энергия системы. Две первые меры являются векторными, а последняя – скалярной).

В механике внешними силами по отношению к данной системе материальных точек называются те силы, которые представляют собою действие на эту систему других тел (других систем материальных точек), не включенных нами в состав данной системы.

Внутренними силами являются силы взаимодействия между отдельными материальными точками данной системы.

3. Замкнутые и незамкнутые системы (смотри лекцию в тетради).

Замкнутые системы — системы, на которые не действуют внешние силы или их действием можно пренебречь. Понятие замкнутой системы является идеализацией, оно применимо к реальным системам тел в тех случаях, когда внутренние силы взаимодействия тел системы значительно больше внешних сил.

Законы сохранения в замкнутых системах

В замкнутой системе выполняются 3 закона сохранения: закон сохранения импульса р=∑рi=Const, момента импульса L=∑Li=Const, и полной энергии E=Емех+Евнутр=Const. Когда систему тел нельзя считать замкнутой, применимы частные законы сохранения, действующие при некоторых дополнительных условиях.

В физике замкнутой системой называется такая система, в которой сохраняется энергия. Эта система не обменивается энергией с окружающим миров и поэтому она не взаимодействует с окружающим пространством и не обменивается с ним ни энергией ни веществом.

В реальности абсолютно замкнутых систем не существует. Это теоретическая абстракция применяется, когда взаимодействие системы с окружающим пространством много меньше, чем взаимодействия внутри замкнутой системы.

Вопрос: Закон сохранения и изменения импульса. Закон сохранения проекции импульса.

Ответ:

1. Закон сохранения и изменения импульса (смотри лекцию).

  Импульс частицы - это произведение ее массы на скорость  . Другое название этой величины - количество движения. Опыт и соответствующий анализ механических явлений показывают, что механическое движение тел характеризуется двумя величинами, которые являются основными мерами механического движения тел: первая - скалярная, вторая - векторная. Это кинетическая энергия   и импульс частицы  .Обе они играют центральную роль во всем построении механики.

Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.

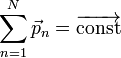 (постоянный вектор).

Суммарный импульс системы частиц есть величина постоянная.

Также стоит подчеркнуть, что изменение импульса   зависит не только от действующей на тело силы, но и от продолжительности её действия.

Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.