Лабораторная работа № 23 законы теплового излучения для вольфрама

Цель работы

Изучение законов теплового излучения.

Основы теории

Электромагнитное излучение всех длин волн связано с колебаниями электрических зарядов, входящих в состав вещества и сопровождается потерей энергии. Для того, чтобы обеспечить возможность длительного излучения энергии, необходимо каким-либо способом пополнять ее убыль. Эти способы могут быть весьма разнообразны, поэтому и характер свечения тел может быть различен.

Одной из наиболее простых и практически важных является ситуация, когда тело заставляют светиться, просто сообщая ему необходимую энергию нагреванием. Этот вид свечения наиболее распространен и называется тепловым излучением. Тепловое излучение можно выделить среди всех прочих видов излучения (хемолюминисценция, фотолюминисценция, электролюминисценция и т.д.), поскольку только тепловое излучение может быть равновесным, то есть может находиться в состоянии теплового равновесия с веществом.

Для равновесного теплового излучения установлен ряд законов теплового излучения, из которых важнейшими являются закон Кирхгофа и закон излучения Планка. Чтобы сформулировать эти законы, следует предварительно ввести некоторые важные понятия.

Лучепоглощательной способностью тела называется отношение мощности поглощенного телом излучения к мощности падающего на поверхность тела излучения :

. (1)

Разумеется, это отношение зависит от материала тела¹ и от его температуры, а также от длины волны излучения. Поэтому в обозначении лучепоглощательной способности имеются индексы (правильнее было бы писать их в качестве аргументов функции; в виде индексов их пишут по исторически сложившейся традиции). Лучепоглощательная способность любого тела находится в интервале от нуля (когда тело отражает всё падающее на него излучение данной длины волны) до единицы (когда тело поглощает все падающее на него излучение данной длины волны).

По лучепоглощательной способности выделяют два предельных (идеализированных) случая - абсолютно черное и абсолютно белое тело. Абсолютно черным называют тело, лучепоглощательная способность которого при любой длине волны равна единице, а абсолютно белым - тело, лучепоглощательная способность которого при любой длине волны равна нулю. Происхождение этих названий в бытовом смысле очевидно - черное тело потому и черно, что почти весь падающий на него свет поглощается, а белое тело бело потому, что при освещении белым светом (содержащим в определенной пропорции излучение со всеми длинами волн) оно отражает почти все падающее на него излучение и отраженное излучение содержит в той же пропорции излучение со всеми длинами волн.

Разумеется, абсолютно черных или абсолютно белых тел в природе не существует. В оптическом диапазоне неплохим приближением к абсолютно черному телу является сажа ( ) или платиновая чернь ( ). В экспериментах в качестве модели абсолютно черного тела обычно используют излучение из небольшого отверстия в замкнутой полости. Для того, чтобы понять, почему это пустое отверстие так черно, достаточно заметить, что падающее на него излучение выходит наружу только после достаточного количества переотражений от стенок полости, в процессе которых оно существенно ослабляется даже в том случае, когда коэффициент поглощения при одном отражении невелик². Вероятно, все видели «непроглядную черноту» входа в неосвещенный подъезд. Этот вход - неплохая модель абсолютно черного тела, как, кстати, и открытое окно в комнате - это ведь тоже относительно небольшое отверстие в замкнутой полости комнаты.

Теперь пора вспомнить, что тело (в том числе и абсолютно черное) может не только отражать падающее на него излучение, но и испускать свое собственное. Эта способность тела и называется его лучеиспускательной способностью. Итак, лучеиспускательной способностью тела называется количество лучистой энергии, испускаемое (во всех направлениях) в единицу времени с единицы площади поверхности тела в единичном спектральном интервале, то есть

. (2)

Подчеркнем, что лучеиспускательная способность (в отличие от лучепоглощательной) является размерной величиной и измеряется в Вт/м³. Формулу (2) можно переписать в виде . Теперь видно, что эта формула просто показывает, что мощность излучения в диапазоне длин волн от до с площадки площадью пропорциональна ширине диапазона длин волн и площади площадки , а коэффициент пропорциональности называется лучеиспускательной способностью тела. Разумеется, лучеиспускательная способность тела зависит от его материала, от длины волны (на разных длинах волн тело излучает по-разному) и от температуры тела (ясно, что горячее тело излучает сильнее холодного). Это обстоятельство и отражают нижние индексы (которые на самом деле логичнее было бы считать просто аргументами функции, как и у лучепоглощательной способности).

Итак, любое тело с точки зрения поглощения и излучения электромагнитного излучения характеризуется двумя функциями длины волны и температуры - лучепоглощательной и лучеиспускательной способностью. Закономерно возникает вопрос - не связаны ли эти функции между собой. Ответ на этот вопрос оказывается положительным и дается законом Кирхгофа, который гласит: отношение лучеиспускательной и лучепоглощательной способности любого тела есть универсальная (не зависящая от рода тела) функция длины волны излучения и температуры. Эта функция является лучеиспускательной способностью абсолютно черного тела.

, (3)

где введено обозначение для лучеиспускательной способности абсолютно черного тела.

Важность этого закона очевидна³ - ведь теперь вместо двух функций (которые в общем случае приходится измерять экспериментально) осталась только одна (например, лучепоглощательная способность), а вторая (например, лучеиспускательная способность) выражается через нее и универсальную функцию - лучеиспускательную способность абсолютно черного тела.

Но в этой бочке меда (для теоретиков начала двадцатого века) таилась и преизрядная ложка дегтя. Дело в том, что саму лучеиспускательную способность абсолютно черного тела очень хорошо и очень точно измерили экспериментально⁴, но никак не могли «вывести» теоретически. Даже хуже того - выводили, и неоднократно, но результат с экспериментом никак не совпадал. Представляете, как обидно? Решить эту задачу удалось только Максу Планку, причем дорогой ценой - для того, чтобы вывести теоретически формулу для лучеиспускательной способности абсолютно черного тела, ему пришлось ввести понятие о квантах света (с чего и началась эпоха квантовой физики!) и постоянную Планка.

Вот эта знаменитая формула - формула Планка:

. (4)

В формуле (4) Дж·сек - постоянная Планка, м/сек - скорость света, -длина волны излучения, Дж/К - постоянная Больцмана. Постоянная Планка впервые появилась именно в формуле (4) и ее числовое значение было определено лично Максом Планком путем подгонки этой формулы (полученной им теоретически) под экспериментальные результаты.

На рис. 1 приведены графики функции Планка при некоторых температурах тела (близких к тем, с которыми Вам придется иметь дело при выполнении лабораторной работы).

Рис. 1.

Зависимость лучеиспускательной способности абсолютно черного тела от длины волны (в Ангстремах, 1 А =10^-8 см).

Из рис. 1 видно, что с ростом температуры тела возрастает излучение этого тела (на всех длинах волн) и максимум излучения перемещается в сторону коротких волн. Количественная формулировка этих фактов содержится в законе Стефана-Больцмана и законе смещения Вина соответственно. Оба этих закона легко получить из формулы Планка (интегрированием и дифференцированием соответственно), хотя на самом деле исторически все происходило как раз наоборот - эти законы были открыты раньше формулы Планка.

Закон Стефана-Больцмана позволяет найти так называемую интегральную лучеиспускательную способность абсолютно черного тела, то есть количество лучистой энергии, испускаемое (во всех направлениях) в единицу времени с единицы площади поверхности тела:

. (5)

Сравнив формулы (2) и (5), нетрудно заметить, что

, (6)

что и оправдывает слово «интегральная» в названии этой величины. Ясно, что интегральная лучеиспускательная способность - это просто мощность излучения с единицы площади тела.

Согласно закону Стефана-Больцмана интегральная лучеиспускательная способность абсолютно черного тела равна произведению постоянной Стефана-Больцмана Вт/(м²·К⁴) на четвертую степень абсолютной температуры тела:

. (7)

Рис. 2.

Зависимость интегральной лучеиспускательной способности абсолютно черного тела от температуры.

Существенно, что закон Стефана-Больцмана справедлив только для абсолютно черного тела. Интегральная лучеиспускательная способность реальных тел меньше, чем у абсолютно черного тела. Это вполне естественно - ведь излучение реального тела на любой длине волны (по закону Кирхгофа) меньше, чем у абсолютно черного, поэтому и суммарное (по всем длинам волн) излучение у него меньше. Для характеристики отличия интегральной лучеиспускательной способности реальных тел от абсолютно черного вводят корректировочный коэффициент , который по определению равен отношению интегральной лучеиспускательной способности данного тела к интегральной лучеиспускательной способности абсолютно черного тела:

. (8)

Часто коэффициент называют интегральной степенью черноты тела при данной температуре. Конечно, степень черноты тела зависит не только от материала тела, но и от температуры. Впрочем, его зависимость от температуры обычно достаточно слаба (по сравнению с зависимостью лучеиспускательной способности) и этой зависимостью часто можно пренебречь. Типичные значения степени черноты для некоторых материалов приведены в таблице 1 Приложения.

На рис. 2 приведен график зависимости интегральной лучеиспускательной способности абсолютно черного тела от температуры.

Закон смещения Вина позволяет найти длину волны, на которой излучение абсолютно черного тела при данной температуре максимально . Согласно закону Вина

, (9)

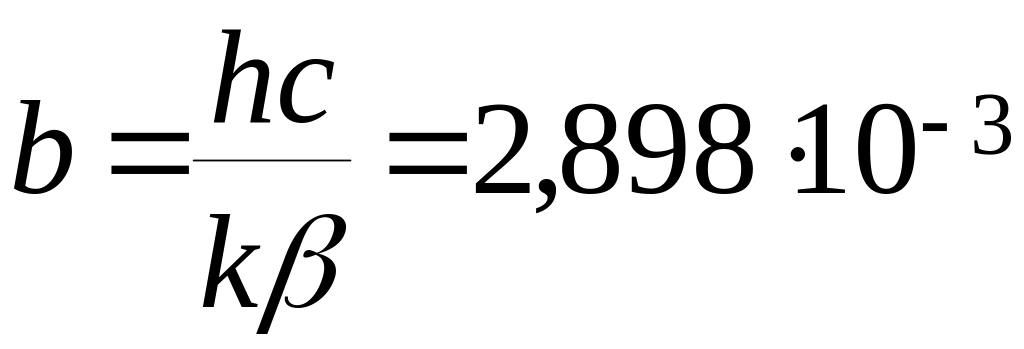где м·К.

Законы теплового излучения для реального тела отличаются от законов для абсолютно черного тела. Очевидно, они имеют вид

. (10)

(закон излучения Планка) и

. (11)

(закон Стефана-Больцмана). Для того, чтобы пользоваться этими законами, необходимо знать зависимость лучепоглощательной способности данного тела (материала⁵) от температуры и длины волны излучения, а также зависимость интегральной степени черноты от температуры. Поэтому законы теплового излучения для реальных тел отличаются от законов для абсолютно черного тела. Впрочем, качественного отличия здесь нет; в этом Вам и следует убедиться при выполнении данной лабораторной работы.

Описание установки.

Рис. 3.

Блок-схема установки.

Рис. 4.

Общий вид установки.

Блок-схема экспериментальной установки изображена на рис. 3. Конструктивно вся установка выполнена в одном блоке (см. рис. 4). Внутри него находится лампочка (с вольфрамовой нитью накаливания, которая и является телом, тепловое излучение которого Вам предстоит изучать), светофильтр (предназначенный для выделения из общего излучения лампочки определенных участков спектра), фотоэлемент (предназначенный для измерения мощности теплового излучения, прошедшего через светофильтр) и мультиметр (предназначенный для того же самого, потому что сам по себе фотоэлемент просто вырабатывает фото-ЭДС, пропорциональную падающему на него световому потоку, а мультиметр измеряет это фото-ЭДС).

В принципе мультиметр – это просто вольтметр, который измеряет фото-ЭДС фотоэлемента (в вольтах, милливольтах или других единицах для измерения напряжения). Но нас интересует не фото-ЭДС фотоэлемента как таковая, а мощность излучения с единицы площади поверхности нити накаливания (в Вт/м²). Ясно, что эти две величины пропорциональны друг другу (если в 2 раза увеличится лучеиспускательная способность, а все остальное не изменится, то и фото-ЭДС возрастет в 2 раза), но чему равен коэффициент пропорциональности – неясно.

Вычислить его теоретически можно, но очень сложно (для этого следует проследить весь путь света от нити лампы до фотоэлемента, учесть все потери световой энергии и знать чувствительность фотоэлемента). Измерить его экспериментально гораздо легче – надо просто вставить вместо нашей лампочки в установку специальную лампу с хорошо известными (то есть измеренными кем-то заранее) излучательными свойствами и посмотреть, что показывает мультиметр. Если, например, при заранее известной мощности излучения с единицы поверхности в 30 Вт/см² наш мультиметр показывает 1,285 единиц мультиметра (е.м.), то 1 е.м.=(30/1,285) Вт/см². Если после этого для другой (неисследованной) лампочки мультиметр показывает 2,435 е.м., то это означает, что ее мощность излучения с единицы площади поверхности равна 2,435 (30/1,285) Вт/см². Этот путь называется градуировкой прибора; он гораздо проще и потому используется гораздо чаше. А самый простой (и потому самый распространенный) путь (которым будем пользоваться и мы при выполнении лабораторной работы) – это вообще не интересоваться, чему равна одна единица мультиметра и измерять все в этой (пусть нам и неизвестной, но существующей в природе) единице измерения. Это – так называемые относительные (а не абсолютные) измерения. Именно результаты таких измерений записываются в «отн. ед.» (относительные единицы) или в «пр. ед.» (произвольные единицы). Не следует думать, что относительные измерения не имеют смысла. Конечно, они менее информативны, чем абсолютные. Тем не менее и они представляют интерес. Если, например, показания мультиметра изменились с 1,34 е.м. до 2, 68 е.м., то мы можем с уверенностью сказать, что лучеиспускательная способность нити возросла в 2 раза (хотя и не можем, увы, сказать, чему именно она была равна и чему именно она стала равна).

В данной лабораторной работе мы будем изучать тепловое излучение раскаленного тела – вольфрамовой нити накала лампы накаливания. Номинальная мощность лампочки – 50 Вт, номинальное напряжение питания – 12 В. Реальное напряжение питания регулируется ступенями по 2 В (переключатель установлен на передней панели установки и позволяет изменять напряжение питания от 0 В до 10 В). В данной установке не предусмотрено измерение реальной температуры нити накаливания – вероятно, оно составляет около 2000 градусов Цельсия. Очевидно, что чем больше подведенное к лампочке напряжение, тем больший ток протекает через ее нить накала и тем горячее нить.

Излучение лампочки пропускается через один из шести светофильтров, установленных на общем диске, край которого расположен на передней панели установки. Этот диск можно поворачивать, устанавливая напротив лампочки один из светофильтров (номер установленного при данном положении диска светофильтра указан на выступающем из ящика краю диска). Параметры светофильтров приведены в таблице 1.

Таблица 1. Параметры светофильтров.

Номер светофильтра	Центральная длина волны , нм	, нм
1	600	2,93
2	1000	3,67
3	1300	1,6
4	1600	1,65
5	2000	2,67
6	Нейтральный светофильтр	-

В первом столбце этой таблицы приведены номера светофильтров (которые указаны на барабане светофильтров), во втором столбце - их центральные длины волн (то есть те длины волн, на которых коэффициент пропускания светофильтра максимален), в третьем – произведение коэффициента пропускания данного светофильтра на центральной длине волны на ширину его полосы пропускания по уровню половины от максимума (см. рис. 5). Обычно это произведение отождествляется с площадью под кривой пропускания, то есть с (то есть площадь под кривой приблизительно заменяется на площадь затемненного на рисунке прямоугольника).

Рис. 5.

Зависимость коэффициента пропускания светофильтра от длины волны ( ). Показан светофильтр с максимальным коэффициентом пропускания 0,32 (32%), центральной частотой 1200 нм и шириной полосы пропускания на уровне половины максимума в 32 нм.

Нейтральный светофильтр не селективен по частоте и предназначен для измерения интегрального по частоте (общего) светового потока. В идеале он не имеет центральной частоты и его ширина бесконечна.

Поскольку фотоэлемент измеряет (в «единицах мультиметра») мощность падающего на него светового потока (перед этим прошедшего через светофильтр), то на самом деле он измеряет величину . Если предположить, что в пределах полосы пропускания светофильтра лучеиспускательная способность вещества изменяется незначительно (а это действительно так), то под знаком интеграла можно заменить на постоянную величину и вынести эту постоянную величину из-под знака интеграла. В результате имеем

,

откуда следует

. (12)

Это означает, что, поделив показания мультиметра для данного светофильтра (с заданным значением центральной частоты , ширины полосы пропускания и коэффициента пропускания в центре полосы пропускания ) на произведение , мы получаем значение лучеиспускательной способности вещества на данной частоте в относительных (или условных, или произвольных – кому как нравится) единицах (у.е. = е.м./нм).

Теперь ясно, как мы можем измерить (в у.е.) зависимость лучеиспускательной способности вольфрама от длины волны. Для этого достаточно при одной и той же температуре вольфрамовой нити измерить показания мультиметра при разных светофильтрах и поделить эти показания на параметры соответствующих светофильтров , приведенные в таблице 1.

Мы можем даже изучить зависимость лучеиспускательной способности от температуры нити, несмотря на то, что эта температура нам неизвестна. Для этого следует заметить, что эта температура, очевидно, возрастает с ростом мощности, выделяющейся на нити накала, а мощность растет с ростом поданного напряжения. Поэтому график зависимости лучеиспускательной способности от поданного напряжения можно рассматривать как неравномерно растянутый вдоль оси напряжений график зависимости лучеиспускательной способности от температуры нити накала (в относительных единицах). Нетрудно сообразить, что такая деформация может сильно исказить график, но кое-что она испортить не в состоянии - как ни растягивай график, монотонный рост останется монотонным ростом, монотонное убывание – монотонным убыванием, максимум – максимумом, а минимум – минимумом. Кроме того, если одна кривая идет выше другой, то она будет делать это и после растягивания.

Экспериментальная часть

Порядок выполнения работы

Описание установки

Экспериментальная установка изображена на рис. 6. На передней панели расположены:

Рис. 6.

1 – мультиметр;

2 – переключатель «накал» - регулировка режимов накала вольфрамовой лампы (позиция «0» - лампа выключена);

3 – тумблер включения лампы – «лампа» с индикацией;

4 - тумблер включения установки «сеть» с индикацией;

5 – в прорезь выведена регулируемая диафрагма со светофильтрами:

поз. 1 – интерференционный с/ф с длиной волны около 600 нм;

поз. 2 – интерференционный с/ф с длиной волны около 1000 нм;

поз. 3 – интерференционный с/ф с длиной волны около 1300 нм;

поз. 4 – интерференционный с/ф с длиной волны около 1600 нм;

поз. 5 – интерференционный с/ф с длиной волны около 2000 нм;

поз. 6 – нейтральный светофильтр.

Упражнение 1. Проверка закона Стефана-Больцмана

Цель упражнения 1 - проверить закон Стефана-Больцмана. Правда, единственное, что можно проверить для не абсолютно черного тела при неизвестной температуре тела – это тот факт, что с ростом температуры тела растет и его интегральная лучеиспускательная способность. Этот факт мы и проверим.

Порядок выполнения упражнения:

0. Установите диск светофильтров в положение «6». При этом напротив лампочки устанавливается нейтральный светофильтр и мы измеряем (разумеется, в у.е.) интегральную лучеиспускательную способность вольфрама.

1. Изменяя значения подаваемого на лампочку напряжения, снимите показания мультиметра при разных значениях напряжения и занесите результаты в таблицу 2.

Таблица 2. Проверка закона Стефана-Больцмана.

Подаваемое на лампу напряжение Uлампы, В	Показания мультиметра при использовании нейтрального светофильтра, Uмульт, е.м.
0
2
4
6
8
10

0. Постройте график зависимости интегральной лучеиспускательной способности (в у.е.) от подаваемого на лампу напряжения.

0. Как зависит интегральная лучеиспускательная способность вольфрама от его температуры? (а – при нагревании интегральная лучеиспускательная способность растет; б – при нагревании интегральная лучеиспускательная способность падает; в – при нагревании интегральная лучеиспускательная способность сначала возрастает, а затем, достигнув некоторого максимального значения, начинает уменьшаться).

Упражнение 2. Проверка закона излучения Планка и следствий из него

Цель упражнения 2 - проверить закон излучения Планка. Правда, единственное, что можно проверить для не абсолютно черного тела при неизвестной температуре тела – это следующие качественные факты:

- зависимость лучеиспускательной способности вольфрама от длины волны имеет характерный «горбообразный» вид, то есть имеется некоторая длина волны, при которой лучеиспускательная способность максимальна;

- эта длина волны уменьшается с ростом температуры тела (закон смещения Вина);

- с ростом температуры вольфрама его интегральная лучеиспускательная способность возрастает;

- при любой длине волны с ростом температуры лучеиспускательная способность вольфрама возрастает;

Порядок выполнения упражнения:

0. Установите значение подаваемого на лампочку напряжения U_лампы=0 В. Снимите показания мультиметра при использовании светофильтров 1-5 и занесите результаты в таблицу 3.

1. Установите значение подаваемого на лампочку напряжения U_лампы=2 В. Снимите показания мультиметра при использовании светофильтров 1-5 и занесите результаты в таблицу 3.

2. Установите значение подаваемого на лампочку напряжения U_лампы=4 В. Снимите показания мультиметра при использовании светофильтров 1-5 и занесите результаты в таблицу 3.

3. Установите значение подаваемого на лампочку напряжения U_лампы=6 В. Снимите показания мультиметра при использовании светофильтров 1-5 и занесите результаты в таблицу 3.

4. Установите значение подаваемого на лампочку напряжения U_лампы=8 В. Снимите показания мультиметра при использовании светофильтров 1-5 и занесите результаты в таблицу 3.

5. Установите значение подаваемого на лампочку напряжения U_лампы=10 В. Снимите показания мультиметра при использовании светофильтров 1-5 и занесите результаты в таблицу 3.

Таблица 3. Проверка закона излучения Планка.

Данные мультиметра.

	Показания мультиметра, Uмульт , е.м.
Подаваемое на лампу напряжение Uлампы , В	Свето-фильтр 1	Свето-фильтр 2	Свето-фильтр 3	Свето-фильтр 4	Свето-фильтр 5
0
2
4
6
8
10

0. Непосредственно показания мультиметра не совпадают с лучеиспускательной способностью (даже в у.е., см. формулу (12)). Поэтому далее следует заполнить таблицу 4, в которой вместо непосредственно показаний мультиметра приведены лучеиспускательные способности (значения параметра для каждого фильтра следует взять из таблицы 1).

Таблица 4. Проверка закона излучения Планка.

Лучеиспускательные способности.

	Лучеиспускательные способности, , у.е.
Подаваемое на лампу напряжение Uлампы , В	Свето-фильтр 1	Свето-фильтр 2	Свето-фильтр 3	Свето-фильтр 4	Свето-фильтр 5
0
2
4
6
8
10

0. На одном графике постройте графики зависимости лучеиспускательной способности вольфрама (в у.е.) от длины волны излучения (в нм).

1. Как зависит лучеиспускательная способность вольфрама длины волны излучения? (а – с ростом длины волны лучеиспускательная способность растет; б – с ростом длины волны лучеиспускательная способность падает; в – с ростом длины волны лучеиспускательная способность сначала возрастает, а затем, достигнув некоторого максимального значения, начинает уменьшаться).

2. Как зависит лучеиспускательная способность вольфрама при фиксированной длине волны от его температуры? (а – при нагревании лучеиспускательная способность растет; б – при нагревании лучеиспускательная способность падает; в – при нагревании лучеиспускательная способность сначала возрастает, а затем, достигнув некоторого максимального значения, начинает уменьшаться).

3. Для каждого значения напряжения питания лампочки найдите среднее значение длины волны теплового излучения вольфрама по формуле

. (13)

Результаты занесите в таблицу 5:

Таблица 5. Проверка закона смещения Вина.

Подаваемое на лампу напряжение Uлампы, В	Среднее значение длины волны теплового излучения , нм
0
2
4
6
8
10

0. Постройте график зависимости среднего значения длины волны теплового излучения (в нм) от подаваемого на лампу напряжения (в В).

1. Как зависит среднее значение длины волны теплового излучения вольфрама от его температуры? (а – при нагревании среднее значение длины волны теплового излучения вольфрама растет; б – при нагревании среднее значение длины волны теплового излучения вольфрама уменьшается; в – при нагревании среднее значение длины волны теплового излучения вольфрама сначала возрастает, а затем, достигнув некоторого максимального значения, начинает уменьшаться).

Приложение

Значения интегральной степени черноты некоторых веществ при некоторых температурах

Вещество	Температура	QT	Вещество	Температура	QT
Вольфрам	1300	0,15	Железо	1500	0,11
	2300	0,29	Окись железа	1500	0,89
	3300	0,34	Никель	1500	0,06
Молибден	1300	0,12	Окись никеля	1500	0,85
	2300	0,23	Платина	1500	0,15
Тантал	2300	0,25	Медь (ж.)	1400	0,15
Уголь	1300	0,52	Окись меди	1400	0,15
Серебро	1300	0,04

Контрольные вопросы:

1. Что такое тепловое излучение? Приведите примеры.

2. Что такое абсолютно черное тело? Встречаются ли абсолютно черные тела в природе?

3. Что такое абсолютно белое тело? Встречаются ли такие тела в природе?

4. Что такое лучеиспускательная способность? В каких единицах она измеряется? По какой формуле можно определить лучеиспускательную способность абсолютно черного тела, если известна его температура?

5. Что такое интегральная лучеиспускательная способность? По какой формуле можно ее рассчитать для абсолютно черного тела, если известна его температура?

6. Что такое лучепоглощательная способность тела? В каких единицах она измеряется? В каких пределах она может изменяться?

7. Что такое интегральная степень черноты тела? В каких единицах она измеряется? В каких пределах она может изменяться?

8. Во сколько раз возрастает интегральная лучеиспускательная способность абсолютно черного тела при удвоении его абсолютной температуры?

9. Во сколько раз возрастает интегральная лучеиспускательная способность реального тела при удвоении его абсолютной температуры?

10. Что такое радиационная температура тела? Она больше или меньше его истинной температуры?

11. Сформулируйте закон смещения Вина. Мы проверяем его или не совсем его?

12. Как зависит средняя длина волны теплового излучения тела от его температуры?

13. Каковы возможные опасности при выполнении данной лабораторной работы? Как их избежать?

Литература

1. Савельев И.В. Курс обще физики. В 5-ти кн. Кн. 4. Волны. Оптика. Кн. 5. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. М.: Изд-во Астрель, 2002.

2. Сивухин Д.В. Общий курс физики. В 5-ти т. Т. 4. Оптика. М.: Физматлит, 2002. 792 с.

3. Бутиков Е.И. Оптика. СПб.: Невский диалект, 2003. 480 с.

4. Зайдель А.Н. Ошибки измерений физических величин. СПб.: Изд-во «Лань», 2005. 112 с.

5. Руководство к лабораторным занятиям по физике. Под ред.Л.Л. Гольдина. М.: Наука, 1973. 688 с.

6. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. М.: Высшая школа, 1965. 568 с.

7. Лабораторный практикум по физике. Под ред. А.С. Ахматова. М.: Высшая школа, 1980. 360 с.

8. Лабораторный практикум по общей и экспериментальной физике. Под ред. Е.М. Гершензона и А.Н. Мансурова. М.: Академия, 2004. 464 с.

9. Майсова Н.Н. Практикум по курсу общей физики. М.: Высшая школа, 1970. 448 с.

10. Физический практикум. Электричество и оптика. Под ред. В.И. Ивероновой. М.: Наука, 1968. 816 с.

Содержание:

Введение…….………………………………………………………....................3

Требования безопасной работы студентов в лаборатории «Оптика»..............4

Выполнение работы и оформление отчета.........................................................7

Статистическая обработка результатов измерений...........................................9

Лабораторная работа № 1. Определение показателя преломления стекла при помощи оптической скамьи и сферометра........................................................13

Лабораторная работа № 2. Определение показателя преломления стекла при помощи микроскопа............................................................................................25

Лабораторная работа № 4. Определение показателя преломления жидкости при помощи рефрактометра...............................................................................30

Лабораторная работа № 5. Определение чувствительности фотоэлемента…………………………………………………………………...41

Лабораторная работа № 7. Светотехнические характеристики и световое поле лампы накаливания……………………………………………………….47

Лабораторная работа № 8. Определение длины световой волны методом колец Ньютона………………………………………………………………….57

Лабораторная работа № 9. Определение длины световой волны при помощи дифракционной решетки……………………………………………………….67

Лабораторная работа № 10. Изучение свойств полупроводниковых солнечных элементов…………………………………………………………..81

Лабораторная работа № 13. Определение постоянной

Стефана – Больцмана…………………………………………………………..91

Лабораторная работа № 15. Изучение поляризованного света……………...99

Лабораторная работа № 22. Изучение распределения частиц в гравитационном поле Земли………………………………………………….114

Лабораторная работа № 23. Законы теплового излучения для

вольфрама……………………………………………………………………...123

Литература…………………………………………………..............................144

1 Все знают, что темные поверхности поглощают излучение (и при этом нагреваются) сильнее светлых. Особенно это заметно весной, когда пятна грязи на снегу протаивают. Часто в городе (где много копоти) уже практически нет снега, а поля за городом (на которые копоти садится существенно меньше, чем на «городской» снег) еще почти полностью под снегом.

2 По той же причине внутренние покрытия в концертных залах имеют волнистую или ребристую поверхность, а часто вообще выглядят «дырчато» - при этом стена по отношению к отражению звуковых волн слегка «чернеет», чего и добиваются строители, озабоченные акустическими свойствами помещения.

3 В том числе и для проблем отопления. Ведь теперь Вам ясно, что чем тело лучше поглощает чужие лучи, то есть чем оно чернее, тем оно лучше испускает свои собственные, если нагрето (правило Прево) . Поэтому (с точки зрения улучшения работы отопительных систем) радиаторы следует красить матовой черной краской, а не блестящей белой эмалью (как это часто делается из эстетических соображений). Конечно, эстетика тоже важна, но терять на нее примерно половину тепла (примерно половина теплоотдачи радиатора - лучевая, а другая - конвекционная) - это чересчур. Лучший вариант - краска, которая в видимом диапазоне длин волн выглядит прилично (и не обязательно черна, как сажа), а в инфракрасной области спектра (где в основном излучают радиаторы парового отопления) черна.

4 Это ведь всего одна универсальная функция, а не своя «суверенная» для каждого тела.

5 Эта величина зависит не только от материала, из которого изготовлено тело, но и от характера его обработки – например, лучепоглощательная способность у полированного вольфрама меньше, чем у матированного (с шероховатой поверхностью).

180