Лабораторная работа № 9 определение длины световой волны при помощи дифракционной решетки

Цель работы

Изучение явления дифракции на основе метода зон Френеля, определение длины световой волны при помощи дифракционной решетки.

Основы теории

Характерным для любых волн является их способность загибать за препятствия, т.е. дифрагировать. Однако масштаб дифракции зависит от отношения размеров препятствия к длине волны.

Природа и основные качественные закономерности дифракции света могут быть установлены с помощью следующих двух принципов:

1. принципа Гюйгенса;

2. закона интерференции.

Принцип Гюйгенса и закон интерференции – принцип Гюйгенса-Френеля – позволяют проанализировать явление дифракции. Особенно просто это можно сделать (правда, для случаев, обладающих симметрией) с помощью метода зон Френеля, который состоит в разделении фронта волны на зоны так, что волны от соответственных точек двух соседних зон приходят в точку наблюдения в противофазе и ослабляют при наложении друг на друга.

Рассмотрим прохождение света через круглое отверстие в непрозрачном экране. Точечный источник света и точка наблюдения лежат на одной прямой, проходящей через середину отверстия, которое открывает лишь часть фронта волны, исходящей из точки (рис.1). Обозначим через расстояние от центра отверстия до точки наблюдения . Для определения действия этой волны в точке разделим (мысленно) волновую поверхность на кольцевые зоны Френеля так, чтобы расстояния от краев соседних зон до точки наблюдения отличились на половину длины волны (рис.1):

Рис. 1

(1)

Тогда колебания, пришедшие в точку от соответственных точек двух соседних зон, будут иметь разность хода , т.е. в точку они придут в противоположных фазах.

Амплитуда колебаний, приходящих из отдельной зоны, зависит от площади зоны, расстояния до точки наблюдения и угла наклона между и нормалью к поверхности. Убедимся, что площади зон одинаковы. Обозначим через радиус - той зоны. Из рис. 2 имеем

;

;

;

. (2)

Рис. 2.

Но по (1) расстояние до - той зоны на больше :

,

отсюда

.

Считая, что длина волны много меньше расстояния , приближенно получим

. (3)

После этого равенство (2) принимает вид

. (4)

Площадь поверхности сферического сегмента радиуса равна

.

Подставляя сюда выражение из (4), получим

. (5)

В пределах этого сегмента умещается зон. Отсюда площадь одной зоны

. (6)

Таким образом, площадь зоны не зависит от ее номера , т.е. площади зон одинаковы. Следовательно, амплитуда колебаний, доходящих от отдельных зон до точки наблюдения , зависит лишь от расстояния и угла, который направление составляет с нормалью к поверхности зоны. С увеличением номера зоны расстояние возрастает, возрастает и угол наклона, поэтому амплитуды колебаний , доходящих до точки от отдельных зон, должны монотонно убывать с увеличением номера зоны :

Поскольку фазы колебаний, приходящих в точку от двух соседних зон, противоположны, то амплитуда суммарного колебания , вызванного действием зон, может быть представлена знакопеременным рядом

, (7)

где знак последнего слагаемого положителен при нечетном и отрицателен – при четном. При четном числе зон колебания попарно ослабляют друг друга, и амплитуда суммарного колебания в точке незначительна. При нечетном числе зон действие одной из зон останется неослабленным, и амплитуда больше, чем при четном числе зон. Более точно значение амплитуды суммарного колебания получим, если воспользуемся очевидным преобразованием, разбив, например, в (7) все нечетные члены на два слагаемых ; и т. д.

Тогда при нечетном и четном соответственно получим

; (8)

(9)

Поскольку амплитуда монотонно убывает с возрастанием номера , то приближенно можно положить амплитуду колебаний -той зоны равной полусумме амплитуд, вызванных и зонами:

.

Тогда слагаемые в рядах (8) и (9), выделенные скобками, равны нулю. И, следовательно, при нечетном :

, (10)

а при четном

. (11)

Если число зон велико, то амплитуда колебаний, вызванных и зонами, мало отличаются друг от друга. Отсюда . Таким образом, равенства(10) и (11) принимают вид:

, (12)

где знак «плюс» соответствует нечетному числу зон, а знак «минус» - четному. Таким образом, мы приходим к выводу: свет не распространяется прямолинейно, так как освещенность в точке наблюдения определяется действием не только центральной зоны, но и зоны, не лежащей на прямой, соединяющей источник света, центр отверстия и точку наблюдения.

Если размеры отверстия увеличивать до бесконечности, т.е. оставить незакрытой всю поверхность волнового фронта , то действием последней зоны можно пренебречь и амплитуда суммарного колебания в точке наблюдения окажется равной - так волновая теория объясняет факт прямолинейности распространения света.

Рис. 3

Представим себе щель, освещаемую пучком параллельных лучей (рис.3). Пусть  ширина щели. Каждая точка щели по принципу Гюйгенса является вторичным источником колебаний, распространяющихся по всем направлениям. Выберем одно какое-либо направление, например, под углом к нормали к щели, и определим, каков будет результат наложения этих лучей, если свести их в одно место (в фокальную плоскость). Результат будет зависеть от разности хода лучей, исходящих от всех точек вторичных центров колебаний, принадлежащих общей для всех лучей волновой поверхности (для параллельных лучей фронт волны - плоскость). Между крайними лучами пучка и разность хода определяется отрезком . Если эта разность хода равна четному числу полуволн, например, двум, то весь пучок можно разбить на два пучка и , в которых каждые два соответственных луча, например и или и , будут иметь разность хода в полволны и поэтому уничтожатся, следовательно, освещенность в точке наблюдения будет минимальной. Если разность хода между крайними лучами равна нечетному числу полуволн, например трем, то весь пучок можно разбить на три пучка с соответственными лучами, разность хода между которыми равна полуволне. Лучи двух пучков уничтожатся при наложении, а третий в фокальной плоскости линзы даст светлую полосу.

Итак, результат наложения друг на друга лучей, идущих от щели под углом к нормали, зависит от разности хода между крайними лучами. Для углов , удовлетворяющих условию

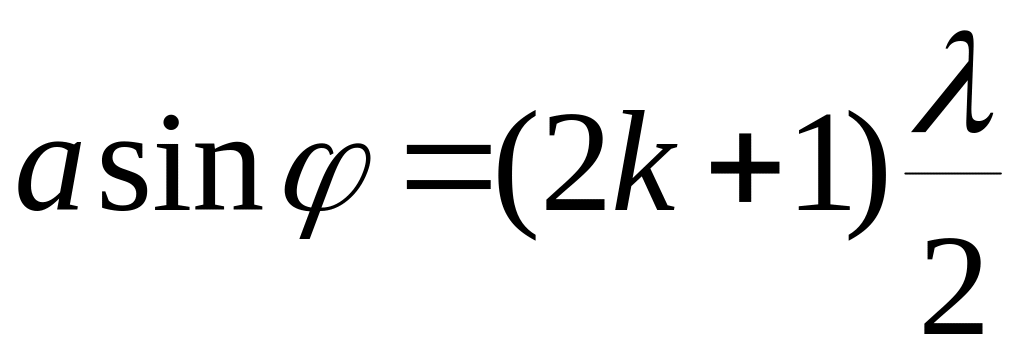, (13)

где в фокальной плоскости линзы будут наблюдаться светлые полосы - максимумы интенсивности, а для углов , удовлетворяющих условию

или , (14)

где , минимумы освещенности.

Дифракционная решетка представляет собой совокупность щелей одинаковой ширины, разделенных темными промежутками.

Дифракционные решетки получают с помощью специальных делительных машин, в которых на стекле алмазом на равном расстоянии наносятся прямолинейные бороздки – штрихи. Число таких штрихов может достигать 15000-16000 на сантиметр. Если дифракционную решетку освещать пучком параллельных лучей, то через неповрежденную алмазом часть стеклянной пластины лучи пройдут, а бороздки будут рассеивать свет и окажутся непрозрачными участками решетки.

Дифракционную решетку принято изображать штриховой линией: черточка означает непрозрачную часть, а просвет-щель. Решетка характеризуется периодом, равным ширине просвета « » плюс ширина бороздки « », т.е. (период решетки есть величина, обратная числу штрихов на единицу длины). Представим себе, что дифракционная решетка освещается пучком параллельных лучей, перпендикулярных к ее плоскости. От каждой щели будут распространяться лучи по всем направлениям. Если на пути этих лучей поместить линзу, а в ее фокальной плоскости экран, то в каждой точке экрана будут собираться все параллельные лучи всех пучков, распространяющихся от щелей дифракционной решетки под одним и тем же углом к нормали. Освещенность в каждой точке экране будет зависеть от интенсивности каждого пучка, собираемого линзой, и от результата интерференции этих пучков при наложении их друг на друга. Если общее число щелей , то интерферирует между собой пучков. Результирующая интенсивность лучей одного пучка, как было при рассмотрении дифракции от одной щели, зависит от угла . Для пучков, вышедших из разных щелей под одним и тем же углом , она будет одинакова.

Будет одинаковой и амплитуда результирующих колебаний в этих пучках, так как интенсивность пропорциональна квадрату амплитуды. Результат интерференции таких пучков зависит от разности фаз, с которой пучки накладываются друг на друга. При монохроматическом источнике света разность фаз в точке встречи будет зависеть от разности хода соответственных лучей (например, крайних) этих пучков и длины волны.

Из рис.4 видно, что (разность хода). Если эта величина равна четному числу полуволн (целому числу длин волн), то соседние пучки накладываются друг на друга в одинаковых фазах и амплитуда результирующих колебаний будет равна сумме амплитуд колебаний, создаваемых лучами одного пучка. В этом месте экрана образуется светлая полоса.

Итак, при освещении решетки монохроматическим светом на экране в фокальной плоскости линзы будут видны светлые полосы там, где собираются лучи, распространяющиеся под углом к нормали, удовлетворяющим уравнению

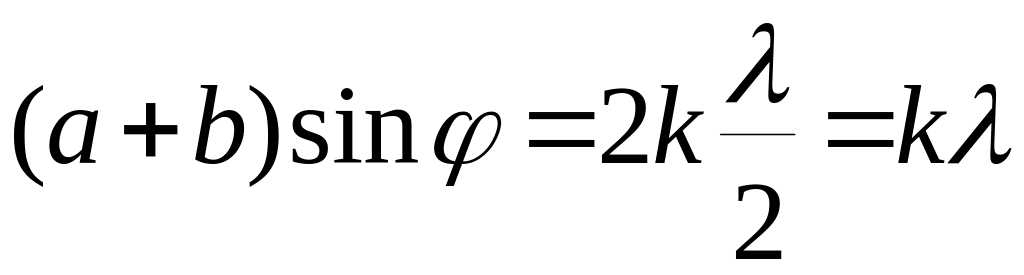, (15)

Рис. 4.

Число таких полос определяется из условия

1.

Например, для лучей с длиной волны 600 нм при 5000 штрихов на 1см решетки, то есть = 1см/5000 = 2∙10⁷ нм будут видны следующие линии: центральная, соответствующая значению ; две линии первого порядка, симметрично расположенные по обе стороны от центральной и образованная лучами, составляющими с нормалью угол

,

две линии второго порядка, соответствующие углу

,

и две линии третьего порядка, соответствующие углу

.

При освещении решетки белым светом в центре ( ) возникает белая полоса, т.к. при условие удовлетворяется при любых длинах волн .

Слева и справа от центральной полосы возникнут максимумы для различных длин волн под углами, значение которых определяется равенством (15) при ; эти максимумы, сливаясь друг с другом, образуют окрашенные полосы – так называемый спектры. В каждом из спектров максимумы фиолетовых лучей расположены ближе всех к центральной полосе, максимумы красных – дальше всех от нее (рис.5).

Рис. 5

В результате при возникают два спектра первого порядка: левый и правый, расположенные своими концами центральной полосе. Аналогично при возникнут спектры второго, третьего и т.д. порядков, расположенные симметрично относительно центральной белой полосы.

Минимальная освещенность при дифракции света от решетки, очевидно, будет иметь место для углов , удовлетворяющих уравнению

, (16)

где .

Чем больше период решетки, тем менее она пригодна для практических целей. Возможность разделять две спектральные линии, мало отличающиеся по длине волны, определяет разрешающую способность дифракционной решетки. Дифракционная решетка является основной частью спектральных приборов, применяемых для спектрального анализа.

Экспериментальная часть

Описание установки:

Для наблюдения спектральных полос и измерения углов дифракции служит спектрометр (рис. 6).

Рис. 6

К горизонтальному лимбу с делениями неподвижно прикреплен коллиматор , на концах которого находится линза и щель . Щель расположена в фокальной плоскости линзы. В центре лимба укрепляется решетка . Лимб снабжен нониусом , соединенным наглухо со зрительной трубой, которая вместе с нониусом может вращаться около вертикальной оси (рис. 7).

Рис. 7

Порядок выполнения работы:

1. Перед щелью коллиматора ставят зажженную неоновую лампу.

2. Зрительную трубу устанавливают так, чтобы ее оптическая ось совпадала с осью коллиматора; при этом точка перекрещивания нитей, видимых в поле зрения трубы, должна лежать на середине центрального изображения щели коллиматора, имеющего одинаковую окраску со светом неоновой лампы.

3. В поле зрения трубы получают центральный максимум (изображение щели), а справа и слева от него спектры первого, второго и третьего порядков. Наводят, перемещая трубу , точку пересечения нитей сначала на середину желтой линии правого спектра первого порядка, делают отсчет по лимбу и нониусу (в градусах и минутах), потом устанавливают точку пересечения нитей на середине желтой полосы левого спектра первого порядка и снова делают отсчет по лимбу и нониусу. Вычитая из первого показания второе, находят двойной угол дифракции для желтой линии спектра первого порядка неона. Деля его значение на два, находят угол дифракции для спектра первого порядка. Совершенно таким же образом находят углы дифракции и для спектров второго и третьего порядков.

4. Вычисляют длину волны желтого света в спектре неона первого порядка по формуле

,

где – период решетки, равный 0,02 мм;

- порядковый номер спектра, равный в данном случае 1. Аналогично вычисляют и по спектрам второго и третьего порядков.

Результаты измерений и вычислений заносят в таблицу.

Таблица

Порядковый номер спектра	Отсчет по лимбу и нониусу для правого спектра	Отсчет по лимбу и нониусу для левого спектра	2				Δ
1
2

Контрольные вопросы

1. В чем заключается явление дифракции?

2. Каким методом можно описать явление дифракции в случаях, обладающих симметрией?

3. Как волновая теория объясняет прямолинейность распространения света?

4. С какой целью доказывается одинаковость площадей зон Френеля?

5. В чем заключаются особенности дифракции света в параллельных лучах?

6. Каким образом осуществляется параллельный пучок лучей в данной работе?

7. Почему спектры, полученные при помощи дифракционной решетки, фиолетовыми концами обращены к центральной полосе? Как объяснить ее происхождение?

8. Сколько всего максимумов (спектров) можно получить с помощью дифракционной решетки?

9. Что такое разрешающая способность дифракционной решетки? Где она применяется?

10. Техника безопасности при выполнении данной работы.