Лабораторная работа №8 определение длины световой волны методом колец ньютона

Цель работы

Изучение явления интерференции света; определение длины волны света методом колей Ньютона.

Основы теории

В 1801 г. английский физик Т. Юнг (1773-1829) впервые на опыте наблюдал явление интерференции света. Это явление состоит в том, что две системы когерентных волн при наложении усиливают друг друга, в тех местах, где гребни волн одной системы попадают на гребни другой, а провалы - на провалы, и ослабляют друг друга в тех местах, где гребни накладываются на провалы. Интерференция - чисто волновое явление.

Р

Рис. 1

ассмотрим опыт Юнга. Пусть малое отверстие в непрозрачном экране (рис. 1) освещается монохроматическим источником света. Согласно принципу Гюйгенса, каждая точка отверстия является источником вторичных волн. Эти волны попадают на два следующих малых отверстия и (во втором непрозрачном экране), которые в свою очередь становятся источниками вторичных волн, перекрывающих друг друга в области , где будет наблюдаться интерференционная картина.

Поскольку колебания в и вызываются одной и той же волной, то они совершаются в одинаковой фазе, т.е. являются когерентным. Колебания в точке и в точке можно представить в виде:

. (1)

Тогда колебания, дошедшие до произвольной точки области от источников и , выразятся следующим образом:

, (2)

здесь и - пути, пройденные колебаниями от и до точки . Амплитуда суммарного колебания определяется соотношением:

, (3)

где - разность фаз.

Е

сли разность фаз равна нулю или , то амплитуда результирующего колебания имеет максимальное значение ( ); когда она равна , амплитуда минимальна ( ). Следовательно, в точке получается максимум или минимум колебаний в зависимости от того, с какой разностью фаз придут колебания от когерентных источников в точку наблюдения. Условие максимума амплитуды в точке имеет вид:

,

отсюда максимум колебаний имеет место при

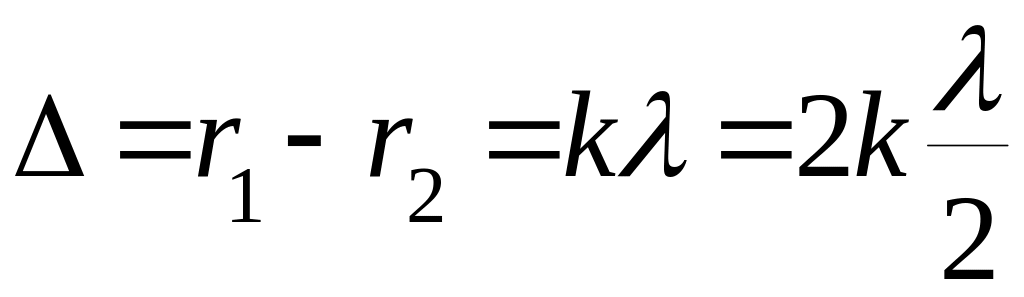. (4)

Волны одинаковой частоты максимально усиливают друг друга при разности хода ( ), равной целому числу длин волн, и ослабляют друг друга, если эта разность равна нечетному числу полуволн

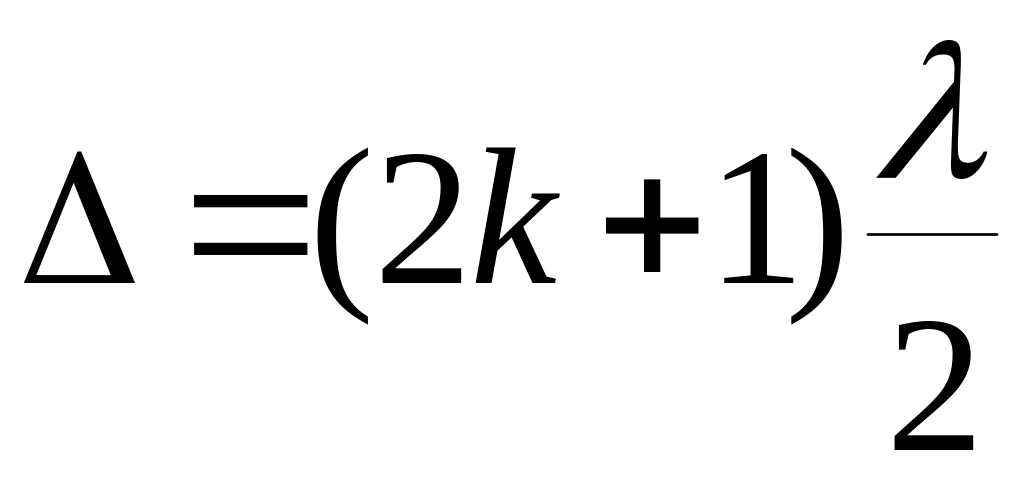; (5)

в (4) и (5) принимает значения .

Явление интерференции также можно наблюдать в тонких пластинках и пленках. Рассмотрим однородную прозрачную пластинку толщиной , плоские поверхности которой параллельны друг другу. Пусть от точечного источника с помощью линзы получается пучок параллельных лучей « ». Этот пучок частично пройдет сквозь пластинку, частично от неё отразится (рис. 2). Поскольку он отразится от обеих поверхностей, возникнут два отраженных пучка с определенной разностью хода. Эти лучи соберутся в точке фокальной плоскости линзы , где будет наблюдаться интерференция.

Рис. 2.

Если показатель преломления материала пластинки , то скорость света в ней . Поэтому время, в течении которого свет проходит расстояние в среде с показателем преломления , определяется соотношением . Произведение геометрического пути на показатель преломления называется оптической длиной пути.

Для подсчета разности хода (рис. 3) выделим из пучка отдельный луч « », падающий на первую поверхность точки под углом .

Рис. 3.

Этот луч частично отразится, образовав луч « », частично преломится и упадет на вторую поверхность пластины в точке . Здесь он снова отразится и преломится. То же произойдет в точке , где возникает преломленный луч « », параллельный лучу « ». Разность хода между этими лучами, с учетом того, что характеризует положение фронта параллельных лучей, будет равна

, (6)

где – оптическая длина пути; – добавочная разность хода, обусловленная изменением фазы колебания на противоположную при отражении от среды оптически более плотной. Этот факт известен в оптике под названием «потери полуволны». Из рис. 3 видно, что

;

.

Пользуясь законом преломления , перепишем выражение для в виде .

Подставляя в (6) вместо , , их значения, для разности хода будем иметь

Но

.

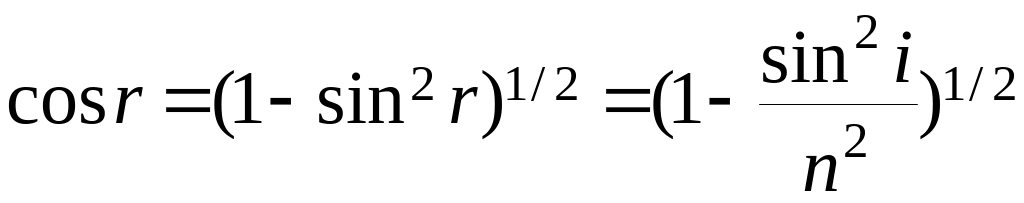Тогда

(7)

представляет в окончательном виде ту разность хода, с которой рассматриваемые лучи сходятся в точке . Если ( ), то в точке будет наблюдаться максимум освещенности; при - минимум.

Рассмотрим теперь прозрачную пластинку, поверхности которой не параллельны, но образуют между собой очень малый (порядка нескольких минут) угол. В этом случае (рис.4) тоже возникают лучи, отраженные от обеих поверхностей и .

Пусть луч « » от точечного источника света в результате отражения от поверхностей и двухкратного преломления у поверхности ведет к образованию луча « », который попадает через линзу в точку , являющуюся изображением точки . Поскольку от источника лучи идут по всевозможным направлениям, то среди них найдется такой луч « », который упадет в эту же точку , где возникнет интерференционная картина. Если угол между поверхностями мал и источник света расположен далеко от пластинки, то разность хода определяется формулой .

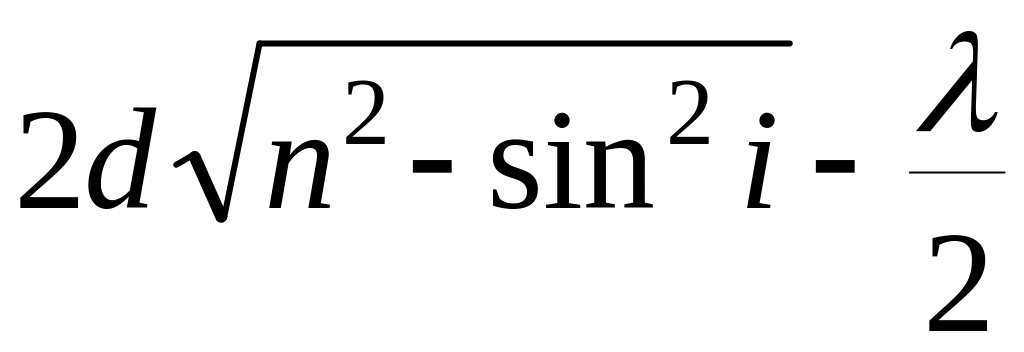Рис. 4

При источнике света, находящемся далеко от пластинки, лучи падают на пластинку приближенно под одинаковыми углами, и тогда разность хода меняется в зависимости только от толщины пластинки . Такие интерференционные полосы называются полосами равной толщины. Эти полосы локализованы на поверхности пластинки и вызывают красивую игру цветов (например, масляные пятна на поверхности воды или асфальте). Характерным примером интерференционных полос равной толщины являются кольца Ньютона.

Плосковыпуклая линза (рис. 5) очень большого радиуса кривизны прижимается выпуклой стороной к плоской пластине так, чтобы между ними образовался воздушный клин переменной толщины. Места одинаковой толщины воздушной прослойки представляют собой окружности равного радиуса. Из прямоугольного треугольника имеем или . Пучок параллельных лучей падает на линзу сверху. Луч, доходящий до точки , частично отражается, а частично проходит в воздушный клин (практически вертикально из-за малой кривизны линзы). Отражаясь в точке от пластинки, луч возвращается обратно и интерферирует с лучом, отраженным в точке . Поскольку в точке происходит отражение от оптически более плотной среды и теряется полволны, то оптическая разность хода обоих интерферирующих лучей ( ) будет равна .

Рис. 5.

Условием образования светлых полос будет являться соотношение , темных - . Чередующиеся светлые и темные полосы представляют собой концентрические кольца. Подставляя в последнее соотношение , получим для радиуса « » - го темного кольца выражение

; (8)

для « » - го

. (9)

Вычитая из (9) (8), получим

.

Откуда

или

. (10)

По формуле (10) вычисляется длина волны .

Экспериментальная часть

Описание установки

У

Рис. 6

становка, применяемая в данной работе, изображена на (рис. 6). S – лампа накаливания с красным светофильтром; К – светофильтр, пропускающий свет длины волны, которую необходимо определить в работе; L₁ – линза, создающая параллельный пучок лучей, М – стеклянная пластинка, которая частично отражает и пропускает свет; Е – стеклянная пластинка, на которой лежит плосковыпуклая линза L; Д – микроскоп с окулярной шкалой. Падающие на пластинку М лучи, отражаясь и проходя через линзу L, попадают на пластинку Е. Интерференционная картина рассматривается в микроскоп. Расположив глаз над окуляром микроскопа, в увеличенном виде наблюдают кольца Ньютона. С помощью окулярного микроскопа производят измерение радиуса колец.

Порядок выполнения работы

1. Включают источник монохроматического света.

2. Направляют пучок монохроматического света через трубку на полупрозрачную пластинку (рис. 7).

3. Фокусируют микроскоп по линзе, добиваясь хорошей видимости.

4. Передвигая линзу с пластинкой на предметном столике микроскопа, находят кольца Ньютона.

Рис. 7

Отсчитывают по окулярному микроскопу радиусы темных колец с номерами: 2,4,6 (к) и 5,7,3 (m) соответственно.

6. По формуле (10) вычисляют длину волны , учитывая, что цена одного деления шкалы микроскопа 2.4∙10^-2 мм. Значение взять у преподавателя.

7. Полученные результаты заносят в таблицу.

Таблица

R	k	m	rk	rm			Δ
	2	5
	4	7
	6	3

Контрольные вопросы

1. Какие источники света называют когерентными?

2. В чем заключается явление интерференции?

3. Что такое оптическая длина пути луча? Чем она отличается от геометрической?

4. В каком случае происходит «потеря полуволны»? Придумайте механическую аналогию.

5. Как объяснить происхождение колец Ньютона? Где они локализованы?

6. Почему в отраженном свете в центре наблюдается темное пятно, а в проходящем – светлое?

7. Если воздушный клин (пространство между линзой и пластинкой) заполнить жидкостью, то как будет выглядеть расчетная формула (10)?

8. Правила техники безопасности при работе с оптическими приборами.