13

Министерство образования РФ

Архангельский государственный технический университет

Кафедра водного транспорта леса и гидравлики

КУРСОВОЙ ПРОЕКТ

по водному транспорту леса

Организация навигационной береговой сплотки лесоматериалов

Выполнил: студент

Факультета ПР

курс IV группа 4

Яшина Е.В.

Проверил:

Суров Г.Я.

Архангельск

2003

Содержание

Задание……………………………………………………………………………3

Введение………………………………………………………………………….4

1. Гидрологические расчеты……………………………………………………5

1.1. Расчет эмпирической кривой, горизонтальных уровней за 6,9,12,15 дней после ледохода…………………………………………………………….5

1.2. Расчет гидрологических характеристик реки…………………………15

2. Обоснование габаритов плотов……………………………………………..17

2.1 Формирование плотов……………………………………………………17

2.1.1. Определение параметров пучков…………………………………...18

2.1.2. Расчет обвязок для пучков…………………………………………..19

2.2 Характеристики секций и их расчет…………………………………...20

2.3 Формирование секций……………………………………………………21

2.4 Формировочный такелаж…………………………………………………22

3.Технология берегового склада………………………………………………25

3.1.Описание технологического процесса………………………………….25

4.Определение объема земляных работ……………………………………...27

5.Расчет крепления плотов…………………………………………………….29

5.1.Выбор типа береговых опор и якорей………………………………….31

6. Расчет количества буксирного флота……………………………………...32

7. Защита плотбища от ледохода……………………………………………..33

8. Расчет потребности рабочих………………………………………………..349. Охрана труда и окружающей среды при береговой сплотке………….35

Литература……………………………………………………………………….37

Введение

Одним из главных резервов повышения эффективности водного транспорта леса, создания экологически чистых технологий является увеличение объемов и повышение технологического уровня береговой сплотки круглых лесоматериалов.

Важнейшим мероприятием по совершенствованию технологии лесосплава является внедрение новых, более экономичных типов плотов, повышение комплексной выработки и улучшение качества сплотки.

Береговая сплотка позволяет избежать потерь леса в сплаве; исключить из транспортного процесса многие виды основных, подготовительных и вспомогательных производств, связанных с проведением молевого сплава; сортировкой и сплоткой леса на воде; сбором разнесенной и подъемом затонувшей древесины. Она создает возможность комплексной механизации и автоматизации производственных процессов; обеспечивает эффективное использование машин и сооружений в течение всего года. Сплотку лесоматериалов организуют на береговых складах, примыкающих к судоходным или временно судоходным водным путям.

Береговой склад – это нижний (затопляемый или незатопляемый) лесной склад в пункте примыкания лесовозной дороги к водному пути.

Работы по береговой сплотке выполняют в едином производственном потоке лесозаготовительных и лесосплавных работ берегового склада. При этом к операции лесозаготовительного цикла на незатопляемых береговых складах добавляются: сплотка лесоматериалов, штабелевка в межнавигационный период, сброска пучков на воду во время навигации и их формирование в секции и плоты.

Целью курсового проекта является детальное изучение технологии береговой сплотки лесоматериалов, и формирование плотов с последующей доставкой их по водным путям потребителям.

1. Гидрологические расчеты

Целью гидрологических расчетов является определение гарантированного водосъемного уровня, продолжительности вывода полотов и отметки заложения дна плотбища.

Под гарантированным съемным уровнем понимают минимальный уровень весеннего половодья, который обеспечивается с вероятностью

95% в течение заданного периода вывода плотов с плотбища.

Гарантированный съемный уровень определяют в результате статистической обработки многолетних водомерных наблюдений по опорному водомерному посту.

1.1 Расчет эмпирической кривой, гарантированных уровней за 6,9,12и15 дней после ледохода.

Из [1(табл.1,прил.3)], устанавливаем для каждого года минимальные уровни весеннего половодья по опорному водомерному посту H_оп. Данные заносим в таблицу 1.

Используя данные из [1(табл.2,прил.4)], строим график связи уровней опорного водомерного поста H_оп и водомерного поста на плотбище H.

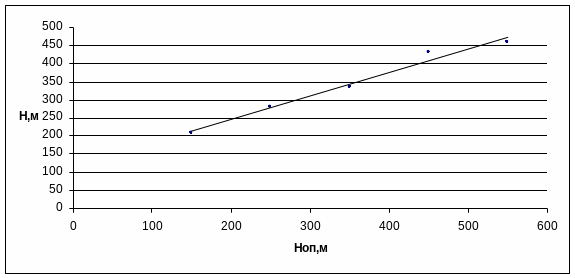
Рис.1 График связи уровней опорного водомерного поста и водомерного поста на плотбище.

По графику связи уровней при известных уровнях для опорного поста H_оп определяют соответственные уровни для водомерного поста на плотбище H. Результаты заносят в таблицу 1.

Соответственные уровни располагают в убывающем порядке, в графе H_i .

Модульный коэффициент вычисляем по формуле;

(1.1)

где H_i- i-е значение уровня убывающего ряда, для 1-го значения

H_i=407см;

H_ср- среднее арифметическое значение ряда уровней.

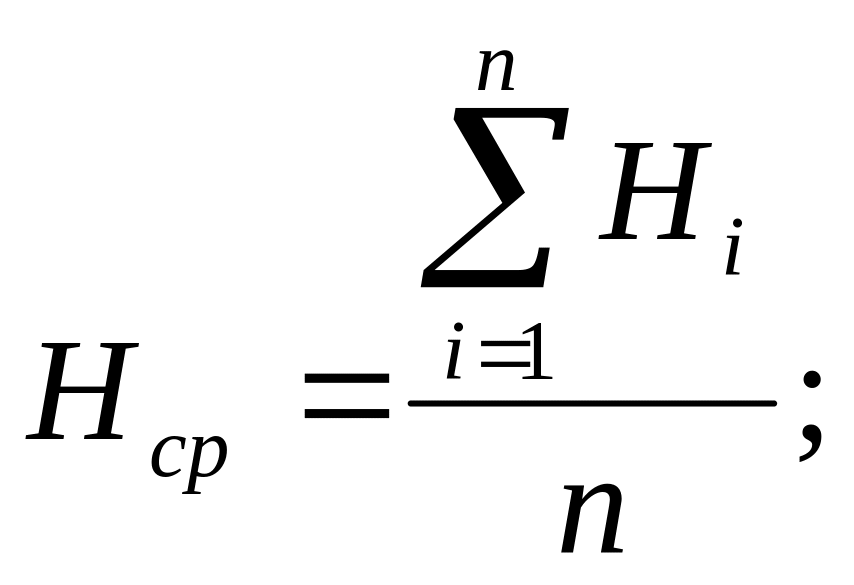(1.2)

где n – количество членов в ряду n=20;

Например модульный коэффициент для первого значения из ряда H_i,

Обеспеченность,%, вычисляем по формуле:

(1.3)

где m- порядковый номер уровня в убывающем ряду

n- число лет наблюдений n=20;

Например: обеспеченность для первого значения убывающего ряда H_i,

Будет равна:

Результаты расчетов сводим в таблицу 1

Талица 1. Расчет эмпирической кривой, гарантированных уровней за

6. дней после ледохода.

Год	Hоп,см	H,см	m	Hi,см	Ki	(Ki-1)	(Ki-1)2	P,%
1971	345	338	1	407	1,250	0,250	0,0625	4,762
1972	350	342	2	400	1,230	0,230	0,0529	9,524
1973	435	400	3	373	1,140	0,140	0,0196	14,286
1974	445	407	4	362	1,110	0,110	0,0121	19,048
1975	300	307	5	359	1,100	0,100	0,0100	23,810
1976	270	286	6	352	1,080	0,080	0,0064	28,571
1977	350	342	7	348	1,070	0,070	0,0049	33,333
1978	395	373	8	342	1,050	0,050	0,0025	38,095
1979	340	335	9	342	1,050	0,050	0,0025	42,857
1980	360	348	10	338	1,040	0,040	0,0016	47,619
1981	365	352	11	335	1,030	0,030	0,0009	52,381
1982	305	311	12	311	0,950	-0,050	0,0025	57,143
1983	195	235	13	307	0,940	-0,060	0,0036	61,905
1984	225	255	14	307	0,940	-0,060	0,0036	66,667
1985	375	359	15	297	0,910	-0,090	0,0081	71,429
1986	245	269	16	290	0,890	-0,110	0,0121	76,190
1987	285	297	17	286	0,880	-0,120	0,0144	80,952
1988	380	362	18	269	0,830	-0,170	0,0289	85,714
1989	300	307	19	255	0,790	-0,210	0,0441	90,476
1990	275	290	20	235	0,720	-0,280	0,0784	95,238
итого				6515	20.00	0,000	0,3716

Определяем коэффициент вариации по формуле:

(1.4)

Коэффициент асимметрии принимаем C_s=2C_v; (1.5)

С_s=2∙0.14=0.28

Правильность расчетов в таблице проверяем по формулам:

условие выполняется;

условие выполняется;

Таблица 2. Расчет эмпирической кривой обеспеченности уровней, гарантированных за 9 дней после ледохода.

Год	Ноп,см	Н,см	m	Hi,см	Ki	(Ki-1)	(Ki-1)2	P,%
1971	325	324	1	393	1,280	0,280	0,0784	7,46
1972	345	338	2	379	1,230	0,230	0,0529	9,52
1973	405	379	3	352	1,140	0,140	0,0196	14,29
1974	425	393	4	345	1,120	0,120	0,0144	19,05
1975	280	293	5	342	1,110	0,110	0,0121	23,81
1976	240	266	6	338	1,100	0,100	0,0100	28,57
1977	325	324	7	338	1,100	0,100	0,0100	33,33
1978	365	352	8	324	1,050	0,050	0,0025	38,10
1979	315	317	9	324	1,050	0,050	0,0025	42,86
1980	315	317	10	317	1,030	0,030	0,0009	47,62
1981	350	342	11	317	1,030	0,030	0,0009	52,38
1982	275	290	12	293	0,950	-0,050	0,0025	57,14
1983	175	221	13	290	0,940	-0,060	0,0036	61,90
1984	205	241	14	286	0,930	-0,070	0,0049	66,67
1985	345	338	15	273	0,890	-0,110	0,0121	71,43
1986	215	248	16	273	0,890	-0,110	0,0121	76,19
1987	250	273	17	266	0,860	-0,140	0,0196	80,95
1988	355	345	18	248	0,810	-0,190	0,0361	85,71
1989	270	286	19	241	0,780	-0,220	0,0484	90,48
1990	250	273	20	221	0,710	-0,290	0,0841	95,24
итого				6160	20,00	0,000	0,4276

Определяем коэффициент вариации по формуле (1.4)

Коэффициент ассиметрии по формуле (1.5)

С_s=2∙0.15=0.30

Правильность расчетов проверяем по условиям:

- условие выполняется;

- условие выполняется;

Таблица 3. Расчет эмпирической кривой, гарантированных уровней

за 12 дней после ледохода.

Год	Ноп,см	Н,см	m	Нi,см	Ki	(Ki-1)	(Ki-1)2	P,%
1971	290	300	1	369	1,270	0,270	0,0729	4,76
1972	320	321	2	352	1,210	0,210	0,0441	9,52
1973	365	352	3	331	1,140	0,140	0,0196	14,29
1974	390	369	4	328	1,130	0,130	0,0169	19,05
1975	245	369	5	328	1,130	0,130	0,0169	23,81
1976	220	252	6	324	1,110	0,110	0,0121	28,57
1977	295	304	7	321	1,100	0,100	0,0100	33,33
1978	330	328	8	304	1,050	0,050	0,0025	38,10
1979	285	297	9	304	1,050	0,050	0,0025	42,86
1980	295	304	10	300	1,030	0,030	0,0009	47,62
1981	335	331	11	297	1,020	0,020	0,0004	52,38
1982	245	269	12	276	0,950	-0,050	0,0025	57,14
1983	160	210	13	269	0,920	-0,080	0,0064	61,90
1984	185	228	14	269	0,920	-0,080	0,0064	66,67
1985	325	324	15	268	0,920	-0,080	0,0064	71,43
1986	195	235	16	252	0,870	-0,130	0,0169	76,19
1987	220	252	17	252	0,870	-0,130	0,0169	80,95
1988	330	328	18	235	0,810	-0,190	0,0361	85,71
1989	255	276	19	228	0,780	-0,220	0,0484	90,48
1990	243	268	20	210	0,720	-0,280	0,0784	95,24
итого				5817	20,00	0,00	0,4177

Определяем коэффициент вариации:

коэффициент ассиметрии:

С_s=2∙0,15=0,30;

Проверяем правильность расчетов:

- условие выполняется;

- условие выполняется;

Таблица 4. Расчет эмпирической кривой, гарантированных уровней

за 15 дней после ледохода.

Год	Ноп,см	Н,см	m	Нi,см	Ki	(Ki-1)	(Ki-1)2	P,%
1971	265	283	1	324	1,180	0,180	0,0324	4,76
1972	290	300	2	324	1,180	0,180	0,0324	9,52
1973	325	324	3	321	1,170	0,170	0,0289	14,29
1974	325	324	4	314	1,150	0,150	0,0225	19,05
1975	220	252	5	310	1,130	0,130	0,0169	23,81
1976	200	238	6	307	1,120	0,120	0,0144	28,57
1977	280	293	7	300	1,090	0,090	0,0081	33,33
1978	310	314	8	293	1,070	0,070	0,0049	38,10
1979	255	276	9	283	1,030	0,030	0,0009	42,82
1980	260	279	10	279	1,020	0,020	0,0004	47,62
1981	305	310	11	276	1,000	0,000	0,0000	52,38
1982	220	252	12	262	0,960	-0,040	0,0016	57,14
1983	145	200	13	262	0,960	-0,040	0,0016	61,90
1984	165	214	14	252	0,920	-0,080	0,0064	66,67
1985	300	307	15	252	0,920	-0,080	0,0064	71,43
1986	190	231	16	241	0,880	-0,120	0,0144	76,19
1987	205	241	17	238	0,870	-0,130	0,0169	80,95
1988	320	321	18	231	0,840	-0,160	0,0256	85,71
1989	235	262	19	214	0,780	-0,220	0,0484	90,48
1990	235	262	20	200	0,730	-0,270	0,0729	95,24
итого					20,0	0,00	0,3560

Определяем коэффициент вариации:

коэффициент ассиметрии:

С_s=2∙0,14=0,28;

Проверяем правильность расчетов:

- условие выполняется;

- условие выполняется;

Таблица 5. Расчет эмпирической кривой обеспеченности по максимальному уровню после ледохода

Год	Ноп, см	Н,см	m	Нi,см	Ki	(Ki-1)	(Ki-1)2	P,%
1971	425	393	1	476	1,220	0,220	0,0484	4,76
1972	435	400	2	459	1,180	0,180	0,0324	9,52
1973	520	459	3	445	1,140	0,140	0,0196	14,29
1974	545	476	4	445	1,140	0,140	0,0196	19,05
1975	370	355	5	442	1,140	0,140	0,0196	23,81
1976	330	328	6	431	1,110	0,110	0,0121	28,57
1977	460	417	7	428	1,100	0,100	0,0100	33,33
1978	500	445	8	417	1,070	0,070	0,0049	38,10
1979	380	362	9	411	1,060	0,060	0,0036	42,86
1980	415	386	10	400	1,040	0,040	0,0016	47,62
1981	450	411	11	393	1,020	0,020	0,0004	52,38
1982	370	355	12	386	0,990	-0,010	0,0001	57,14
1983	290	300	13	362	0,930	-0,070	0,0049	61,90
1984	300	307	14	355	0,910	-0,090	0,0081	66,67
1985	480	431	15	355	0,910	-0,090	0,0081	71,43
1986	295	304	16	328	0,840	-0,160	0,0256	76,19
1987	330	328	17	328	0,840	-0,160	0,0256	80,95
1988	495	442	18	307	0,800	-0,200	0,0400	85,71
1989	500	445	19	304	0,790	-0,210	0,0441	90,48
1990	475	428	20	300	0,770	-0,230	0,0529	95,24
итого				7772	20,0	0,00	0,3816

Определяем коэффициент вариации:

коэффициент ассиметрии:

С_s=2∙0,14=0,28;

Проверяем правильность расчетов:

- условие выполняется;

- условие выполняется;

По рассчитанным значениям и соответствующим уровням Н_i строим эмпирическую кривую обеспеченности в виде ломанных линий.

Из таблицы 3 [2,прил 3] при C_v =0,28 определяем интерполяцией модульные коэффициенты к_р при (Р=1...99%);

К_р1%=1,25+0,027∙6=1,41

Вычисляем уровни разного процента обеспеченности:

Н_р=к_р∙Н_ср (1.6)

Н_р=1,35∙326=440.1см

Результаты расчетов сводим в таблицу 6, а затем на основании этой таблицы строим теоретические кривые обеспеченности в виде плавных кривых, Рис.2.

Рис.2 График теоретических кривых обеспеченности.

Затем на клетчатке вероятностей строим теоретические кривые которые получаются в виде спрямленных линий. Рис 3.

Показатель	Обеспеченность Р,%
	1	5	10	20	30	40	50	60	70	80	90	95	99
Через 6 дней после ледохода Сv=0.28
Кр	1,35	1,24	1,18	1,11	1,07	1,03	0,99	0,96	0,92	0,88	0,83	0,78	0,70
Нр,см	440,1	404,2	384,7	361,9	348,8	335,8	322,7	313,0	299,9	286,9	270,6	254,3	228,2
Через 9 дней после ледохода Cv=0.30
Кр	1,38	1,26	1,20	1,12	1,07	1,03	0,99	0,96	0,92	0,87	0,81	0,77	0,69
Нр,см	425,0	388,1	369,6	344,9	329,6	317,2	304,9	295,7	283,4	268,0	249,5	237,2	212,5
Через 12 дней после ледохода Сv=0.30
Кр	1,38	1,26	1,20	1,12	1,07	1,03	0,99	0,96	0,92	0,87	0,81	0,77	0,69
Нр,см	401,6	366,7	349,2	325,9	311,4	299,7	288,1	279,4	267,7	253,2	235,7	224,1	200,8
Через 15 дней после ледохода Сv=0.28
Кр	1,35	1,24	1,18	1,11	1,07	1,03	0,99	0,96	0,92	0,88	0,83	0,78	0,70
Нр,см	369,9	339,8	323,3	304,1	293,2	282,2	271,3	263,0	252,1	241,1	227,4	213,7	191,8
По максимальному уровню после ледохода Сv=0.28
Кр	1,35	1,24	1,18	1,11	1,07	1,03	0,99	0,96	0,92	0,88	0,83	0,78	0,70
Нр,см	525,2	482,4	459,0	431,8	416,2	400,7	385,1	373,4	357,9	342,3	322,9	303,4	272,3

Таблица 6 Данные для построения теоретической кривой.

По теоретической кривой обеспеченности определяют минимальный съемный уровень маловодного года 95% обеспеченности.

Строим график зависимости съемных уровней от продолжительности их стояния,Рис4, съемные уровни Н_i берем из таблицы 1.6 по 95%-ой обеспеченности.

Предельная продолжительность вывода плотов – 15 суток (по заданию).

Рис.4.График зависимости съемных уровней от продолжительности их стояния