КОНТРОЛЬНЫЕ ВОПРОСЫ ПО СТАТИКЕ

(Первый коллоквиум)

1. Сформулируйте аксиомы статики.

1-ая (равновесия двух сил): Если на свободное абсолютно твёрдое тело действует две силы, то эти силы эквивалентны нулю тогда и только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны.

2-ая (присоединения и исключения): Не изменяя действия системы сил на тело, можно от нее отнять или прибавить к ней любую систему уравновешенных сил.

3-ья (равенства действия и противодействия): Всякому действует соответствует равное по модулю и противоположное по направлению противодействие.

4-ая (параллелограмма): Равнодействующая двух сил по величине и направлению равна диагонали параллелограмма, построенного на этих силах как на сторонах.

5-ая (связи): Любое несвободное тело можно считать свободным, отбрасывая связи и заменяя их действия реакциями.

6-ая: (принцип отвердевания): Равновесие сил, приложенных к нетвердому телу, не нарушается при его затвердевании.

2. Дайте определения равнодействующей и уравновешивающей произвольной системы сил.

Равнодействующая сила – сила, эквивалентная некоторой системе сил.

Система взаимно уравновешивающихся сил – система сил, которая, будучи приложенной к твердому телу, находящемуся в покое, не выводит его из этого состояния.

3. Дайте определение системы сходящихся сил. Как найти равнодействующую системы сходящихся сил графическим методом и аналитически?

Система сходящихся сил – совокупность сил, линии действия которых пересекаются в одной точке.

Графический метод нахождения равнодействующей с.с.с.: равнодействующая по величине и направлению равна замыкающей стороне силового многоугольника, построенного на заданных силах как на сторонах.

Аналитический метод нахождения равнодействующей с.с.с.: если с.с.с. дана так, что известны проекции заданных сил, то при их помощи можно решать задачи на равновесие сходящихся сил, если число неизвестных в задаче не превышает трех.

4. Запишите и сформулируйте условия равновесия системы сходящихся сил в векторной форме, а также в проекциях на оси декартовой системы координат.

Условия равновесия в векторной форме

- Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этой системы сил равнялась нулю.

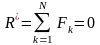
- Если 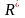- вектор, замыкающий силовой многоугольник: геометрической условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.

Условия равновесия в аналитической форме

- , т.е. 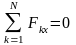, , 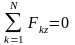. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из трёх выбранных любым образом координатных осей равнялись нулю.

- , . Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из двух выбранных любым образом координатных осей, лежащих в плоскости действия данной системы, равнялись нулю.

5. Сформулируйте теорему о трех уравновешенных силах.

Если тело находится в равновесии под действием трёх сил и линии действия двух из них пересекаются в одной точке, то линия действия третьей силы обязательно проходит через эту точку.

6. Дайте определение алгебраической величины момента силы относительно некоторого центра. Поясните на рисунке как определить плечо силы и знак момента.

Моментом силы относительно точки называется алгебраическая величина,

равная произведению модуля силы на кратчайшее расстояние от точки

до линии действия силы.

Плечо силы – кратчайшее расстояние от точки вращения до линии действия силы.

Если сила вращает тело относительно точки вращения по часовой стрелке, то знак

момента минус, если против – то плюс.

7. Сформулируйте определение и запишите математическое выражение для векторного момента силы относительно некоторого центра.

Момент силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на вектор силы.

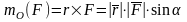
8. Дайте определение момента силы относительно оси и укажите способы его нахождения. Поясните на рисунке данное определение. В каких случаях момент силы относительно оси равен нулю?

- Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярную к данной оси, относительно точки пересечения этой плоскости с осью.

- Момент силы относительно оси равен проекции на эту ось вектора момента силы относительно произвольной точки, лежащей на этой оси.

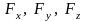- Если сила задана своими проекциями и координатами x, y, z точки приложения, то момент силы относительно начала координат может быть представлен в виде определителя третьего порядка:

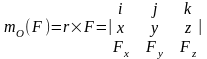
- для определения знака момента, удобно рассматривать систему с положительных направления осей x, y, z и принимать момент положительным, если проекция силы на плоскость, перпендикулярную оси пытается создать вращательный эффект вокруг этой же оси против хода часовой стрелки.

Момент силы относительно оси равен нулю, когда линия действия силы параллельная оси или пересекает её.