3.2. Принцип относительности классической механики

 

            Предположим, что подвижная система отсчета движется поступательно, равномерно и прямолинейно. При этом угловая скорость   и угловое ускорение   подвижной системы координат, а также ускорение ее начала   равны нулю. Следовательно, равны нулю переносное  , кориолосово   ускорения и обе силы инерции  ,  . Теперь уравнение (3.5) примет вид:

.                                            (3.7)

            Сравнивая уравнения (3.1) и (3.7), приходим к выводу о том, что в рассматриваемом случае последнее уравнение, определяющее относительное ускорение материальной точки, совпадает с основным уравнением динамики (3.1), определяющим ее абсолютное ускорение. Таким образом, движение материальной точки относительно системы отсчета, движущейся поступательно, равномерно и прямолинейно, происходит так же, как и относительно неподвижной системы отсчета, т.е. подвижная система является инерциальной.

            Действительно, если правая часть уравнения (3.7) равна нулю, то из него получим  , откуда следует, что точка движется равномерно и прямолинейно, т.е. выполняется 1-й закон динамики. Так как законы динамики одинаковы во всех инерциальных системах отсчета, никакие механические эксперименты, проводимые в инерциальной системе отсчета, не могут обнаружить, находится ли она в покое или движется поступательно, равномерно и прямолинейно. В этом состоит открытый Галилеем принцип относительности классической механики.

 

3.3. Условия относительного покоя. Сила тяжести

 

            Пусть материальная точка под действием приложенных к ней сил находится в состоянии относительного покоя, т.е. не движется относительно подвижной системы отсчета Oxyz. В этом случае относительная скорость   и относительное ускорение   точки равны нулю, следовательно, равна нулю и кориолисова сила инерции  . Уравнение относительного покоя получим из уравнения (3.5)

.                                        (3.8)

            Таким образом, если материальная точка находится в состоянии относительного покоя, геометрическая сумма действующих на нее сил и переносной силы инерции равна нулю. Следует отметить, что выполнения условия (3.8) не означает, что после сообщения точке начальной скорости она будет двигаться равномерно и прямолинейно относительно подвижной системы, как это имеет место в инерциальной системе отсчета. Действительно, при появлении относительной скорости, во-первых, возникает кориолисово ускорение   и кориолисова сила инерции  , во-вторых, может измениться переносное ускорение, зависящее от положения точки в подвижной системе отсчета, что приведет к изменению переносной силы инерции  . Таким образом, правая часть уравнения (3.5) будет отлична от нуля, и точка будет иметь относительное ускорение  .

            Рассмотрим в качестве примера материальную точку М, подвешенную на нити и находящуюся в покое относительно Земли (рис. 3.3). Запишем условие относительного покоя (3.8) и получим

,                                    (3.9)

где   – реакция нити;   – сила притяжения Земли, направленная к ее центру;   – переносная сила инерции, которая вследствие равномерного вращения Земли имеет только центробежную составляющую, направленную от ее оси вращения. Модуль силы инерции

,

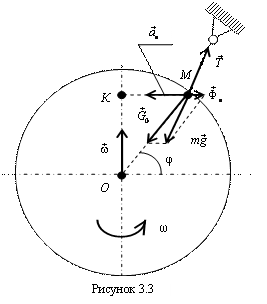
где ρ = МК – радиус географической параллели; R – радиус Земли; ω – угловая скорость вращения Земли; φ – геоцентрическая широта. Силу, равную по модулю и направленную противоположно реакции  , называют силой тяжести и обозначают через  . Таким образом, сила тяжести равна геометрической сумме силы притяжения   и силы инерции  , вызванной вращением Земли:

.

Направление силы тяжести   определяет направление вертикали в данной точке земной поверхности, а плоскость, перпендикулярная силе  , является горизонтальной.

            Сила инерции   очень мала по сравнению с силой тяжести, что видно из отношения их модулей

.

Оно максимально на экваторе (1/290) и равно нулю на полюсе. Отклонение линии отвеса от направления радиуса Земли максимально на широте 45⁰ и составляет  . Таким образом, сила тяжести   и по модулю, и по направлению мало отличается от силы притяжения  . Ускорение свободного падения g максимально на полюсе (9,83 м/с²) и минимально на экваторе (9,78 м/с²).

 2

 Динамика материальной точки. Две основные задачи динамики МТ.