[Править]Абсолютно неупругий удар

Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.

Где v это общая скорость тел, полученная после удара, m_a - масса первого тела, u_a - скорость первого тела до соударения.m_b - масса второго тела, u_b -скорость второго тела до соударения. Важно - импульсы являются величинами векторными, поэтому складываются только векторно.

Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соудареямых тел в результате неупругих деформаций переходит в тепловую.

Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.

 5

3.1. Уравнения относительного движения

 

            Два первых закона динамики и все соотношения, полученные из них, в том числе и основное уравнение динамики

,                                          (3.1)

справедливы только при движении точки относительно инерциальной системы отсчета.

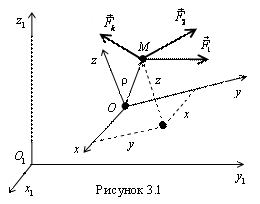             Рассмотрим движение точки M относительно неинерциальной системы отсчета (рис. 3.1). Пусть система  является инерциальной (в дальнейшем будем называть ее неподвижной), а системаOxyz – неинерциальной и дви-жущейся относительной неподвижной системы отсчета. Будем также считать, что переносное движение системы Oxyz и силы, действующие на точку Mизвестны. Воспользуемся теоремой Кориолиса, в соответствии с которой абсолютное ускорение точки   равно геометрической сумме относительного  , переносного   и кориолисова   ускорений:

.                                           (3.2)

Подставляя (3.2) в уравнение (3.1), получим

или

.                              (3.3)

            Введем векторы

                                   (3.4)

называемые переносной и кориолисовой силами инерции, тогда уравнение (3.3) примет вид:

.                                     (3.5)

Оно представляет собой основное уравнение динамики относительного движения материальной точки. Таким образом, если к силам, действующим на материальную точку, условно присоединить переносную и кориолисову силы инерции, то уравнение относительного движения точки (3.5) сохранит форму основного уравнения динамики (3.1).

            Для определения сил инерции необходимо найти соответствующие ускорения точки. Воспользуемся известными из кинематики соотношениями. Переносное ускорение представим как абсолютное ускорение точки, неизменно связанной с подвижной системой отсчета:

,

где   – ускорение начала координат подвижной системы;   – угловое ускорение и угловая скорость подвижной системы;   – радиус-вектор точки в подвижной системе координат. Кориолисово ускорение  , где   – относительная скорость точки. Как следует из выражений (3.4), силы инерции   направлены противоположно ускорениям  .

            Сопоставление уравнений (3.1) и (3.5) показывает, что в инерциальной системе отсчета ускорение материальной точки является лишь результатом действия на нее сил, т.е. взаимодействия с другими телами. В неинерциальной системе отсчета ускорение материальной точки зависит как от действующих на нее сил, так и от движения самой системы отсчета.

            Спроецируем векторное уравнение (3.5) на оси подвижной системы Oxyz и получим дифференциальные уравнения относительного движения материальной точки:

;

;                                   (3.6)

,

где   – проекции относительного ускорения на оси подвижной системы.

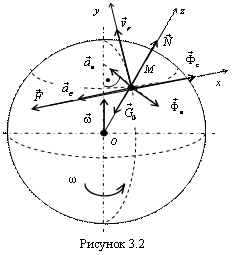             Рассмотрим в качестве примера использования уравнений относительного движения явление размыва берегов рек. Как известно, в северном полушарии правые берега рек, текущих вдоль меридиана, обычно обрывистые, а левые – пологие. Для объяснения этого явления возьмем некоторый объем воды М, заключенный между двумя сечениями реки, текущей с юга на север (рис. 3.2). На этот объем действует сила притяжения Земли  , реакция дна   и реакция берега  . Для записи уравнения движения в неинерциальной системе отсчета, связанной с Землей, введем переносную   и кориолисову   силы инерции. Переносное ускорение   направлено к оси вращения Земли, так как Земля вращается равномерно с угловой скоростью  , а переносная сила инерции – в противоположную сторону. Кориолисово ускорение   направлено на запад, а кориолисова сила инерции – на восток.

            Уравнение относительного движения имеет вид:

.

Спроецируем его на ось Mx, направленную на восток вдоль касательной к параллели, учитывая, что относительное ускорение   лежит в плоскости меридиана, и получим   или  . Таким образом, реакция берега действительно направлена влево, если смотреть по течению реки. Следовательно, сила давления воды, по 3-му закону динамики, действует противоположно, т.е. на правый берег, постепенно его размывая. Это правило не изменяется и для рек, текущих с севера на юг. В южном полушарии, напротив, размываются левые берега рек.