18.2. Коэффициент восстановления при ударе

Импульсы ударных сил зависят не только от масс и скоростей, но и от свойств соударяющихся тел.

Рассмотрим падение шара на неподвижную плиту (рис. 18.2). При этом     − импульс реакции за время удара.

Разделим удар на две фазы:

1. От соприкосновения шара с плоскостью до его полной остановки. Кинетическая энергия шара переходит при этом  в потенциальную энергию упругой деформации  , частично теряясь на необратимое изменение его формы и рассеиваясь в виде тепла.

2. Скорость меняет направление и величину от   до  . При этом накопленная потенциальная энергия переходит в кинетическую энергию    .

Величина, равная отношению скорости точки после удара к ее скорости до удара, называется коэффициентом восстановления при ударе о неподвижную плиту 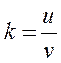      ,   .   Если  , то удар  абсолютно упругий  , если  , то удар абсолютно неупругий  . Коэффициент восстановления определяется экспериментально и в зависимости от материала соударяющихся тел может принимать различные значения:   дерево о дерево …  ,   сталь о сталь …  ,  стекло о стекло …  .

 

Одним из способов определения коэффициента восстановления при ударе может служить определение высоты отскока шара от неподвижной поверхности, падающего на нее с высоты   без начальной скорости (рис. 18.3). Скорость шара в начале удара 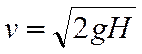    .   В конце удара 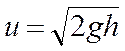   ,   где   − высота, на которую шар поднимется после удара. Тогда 

.

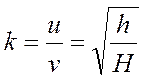Ударной силой называется сила, импульс которой за время удара является конечной

величиной. Модуль ударной силы может в тысячи и даже в десятки тысяч раз превосходить

конечные по модулю силы, например силы тяжести, силы сопротивления воздуха или воды,

силы трения. Импульсы конечных по модулю сил за бесконечно малое время удара будут

бесконечно малы, и ими при изучении удара пренебрегают.

Напомним, что если конечная по модулю сила F действует в течение времени, тау

начиная свое действие в момент времени t, то ее импульс имеет вид

Ударный импульс– это импульс, который вводится при изменении скоростей точек

тела за время , когда вместо самой ударной силы вводится ее импульс. Для определения

ударного импульса S совершаем в соответствии со сказанным выше предельный переход,

устремляя F к бесконечности и – к нулю, т. е.

Абсолютно упругий удар

Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. Вклассической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Математическая модель абсолютно упругого удара работает примерно следующим образом:

1. Есть в наличии два абсолютно твердых тела, которые сталкиваются

2. В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации.

3. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию.

4. Контакт тел прекращается и они продолжают движение.

Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии и закон сохранения импульса.

Здесь m₁, m₂ - массы первого и второго тел. u₁, v₁ - скорость первого тела до, и после взаимодействия. u₂, v₂ - скорость второго тела до, и после взаимодействия.

Важно - импульсы складываются векторно, а энергии скалярно.

Абсолютно упругий удар может выполняться совершенно точно при столкновениях элементарных частиц низких энергий. Это следствие принципов квантовой механики, запрещающей произвольные изменения энергии системы. Если энергии сталкивающихся частиц недостаточно для возбуждения их внутренних степеней свободы, то механическая энергия системы не меняется. Изменение механической энергии может также быть запрещено какими-то законами сохранения (момента импульса, чётности и т. п.). Надо, однако, учитывать, что при столкновении может изменяться состав системы. Простейший пример — излучение кванта света. Также может происходить распад или слияние частиц, а в определённых условиях — рождение новых частиц. В замкнутой системе при этом выполняются все законы сохранения, однако при вычислениях нужно учитывать изменение системы.