0.2. Обобщенные силы. Условие равновесия в обобщенных координатах

Рассмотрим систему, имеющую   степеней свободы, на которую наложены стационарные и голономные связи.   Для введения понятия обобщенной силы рассмотрим сумму виртуальных работ активных сил, действующих на точки данной механической системы: 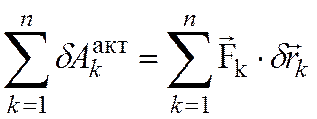   .  Для систем со стационарными связями радиус-вектор  -й точки  есть функция обобщенных координат: 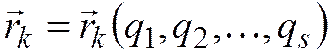   .  Виртуальные перемещения точек механической системы найдем, пользуясь определением полного дифференциала (главной части приращения функции многих переменных)  .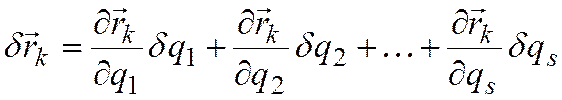 

 Подставляя данное выражение в формулу для выражения работы активных сил, находим:

.

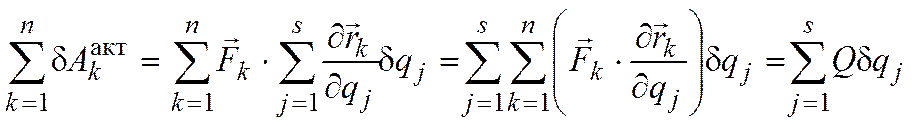Величины 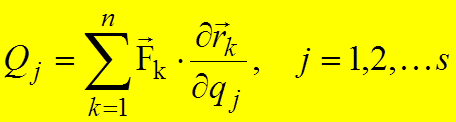   ,  стоящие при соответствующих вариациях обобщенных координат в формуле для вычисления суммы виртуальных работ активных сил, действующих на точки данной механической системы, называютсяобобщенными силами.

 

Размерность обобщенных сил определяется размерностью соответствующих обобщенных координат

  .

 

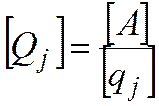Способы вычисления обобщенных сил:  Используя формулу для вычисления скалярного произведения через координаты перемножаемых векторов, обобщенную силу можно записать  в виде 

 

.

 

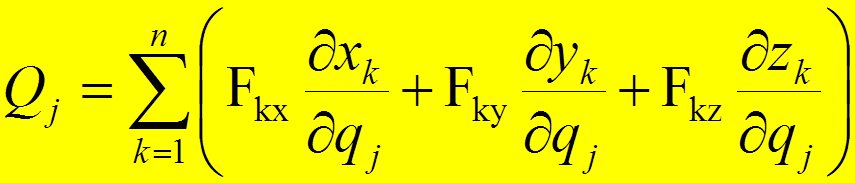Это выражения в конкретных расчетах не используется, а применяется следующий способ.

Так как связи голономные, то вариации обобщенных координат независимы, и обобщенную силу можно найти, задавая изменение лишь одной координаты, а вариации остальных полагать равными нулю. Тогда, определяя виртуальную работу активных сил на изменении этой   координаты, находим

,

    .

 

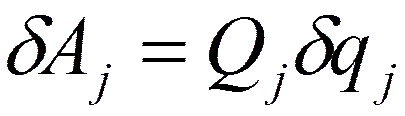Если механическая система консервативная, то обобщенная сила равна частной производной от потенциальной энергии по соответствующей обобщенной координате, взятой со знаком минус

 

  .

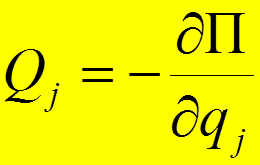Действительно, силы, действующие на точки механической системы, в этом случае определяются равенствами:

,   ,   .

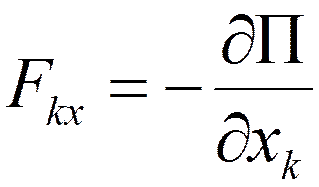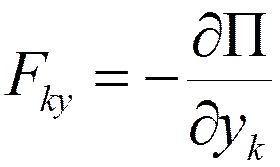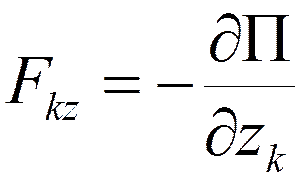 Их подстановка в формулы первого способа определения обобщенных сил дает

.

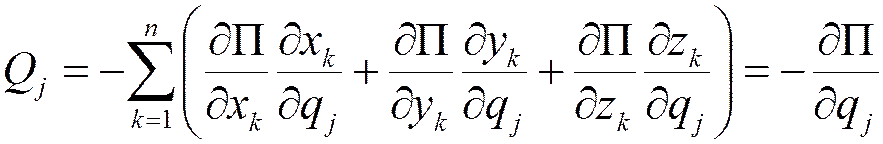В начало лекции

  

 

25 не весь

Условие равновесия в обобщенных координатах  

Согласно принципу виртуальных перемещений, условие 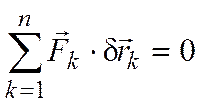    является необходимым и достаточным для равновесия системы с идеальными и стационарными связями. Переходя к обобщенным координатам, находим              .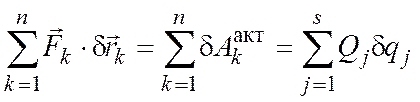

 

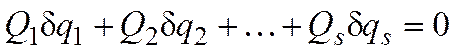Пусть связи, наложенные на систему, являются голономными. В силу независимости вариаций обобщенных координат равенство нулю возможно только в том случае, когда все коэффициенты при вариациях обобщенных координат равны нулю. 

 

Для равновесия механической системы с идеальными, стационарными и голономными связями необходимо и достаточно, чтобы все обобщенные силы были равны нулю

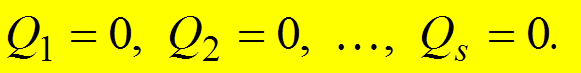
Для консервативных механических систем необходимым и достаточным условием равновесия является система равенств:

  

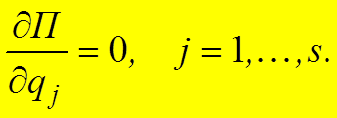
Вычисление обобщённых сил

Если система имеет n степеней свободы, то у неё n обобщённых координат, независимых друг от друга (q₁, q₂, …, q_n) и n возможных перемещений (δq₁, δq₂, …, δq_n). Сумма элементарных работ, приложенных к системе сил, на возможные перемещения системы равна

.

Обобщёнными силами называются коэффициенты, стоящие перед соответственными возможными перемещениями. Так как обобщённые координаты не зависят друг от друга, то для определения обобщённой силы системе необходимо сообщить возможные перемещения, соответствующие координатам, а все остальные возможные перемещения принять за нуль, то есть для определения Q₁ необходимо, чтобы δq₁ ≠ 0, δq₂ = 0, δq₃ = 0, …, δq_n = 0, тогда

  .

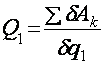Размерность обобщённых сил зависит от размерности обобщённых координат: если q_j = x (м), то Q_j  – сила (Н); если q_j = φ (рад), то Q_j  – момент (Н∙м).

26.

Вводится функция Лагранжа:  L = T – П, тогда    – уравнения Лагранжа второго рода для консервативной системы.

При стационарных связях (связях, не зависящих от времени) t не входит в выражение для кинетической энергии, тогда   – квадратичная форма обобщенных скоростей,  a_ij= a_ji – коэффициенты инерции. Квадратичная форма всегда положительна.

ВЕРНУТЬСЯ   6 Уравнения второго рода для консервативной системы

 

Предположим, что на рассматриваемую механическую систему наряду с силами, имеющими потенциал (консервативными силами), действуют силы, не имеющие потенциала (неконсервативные силы). При этом условии обобщенную силу   удобно представить в виде суммы обобщенной силы  , соответствующей консервативным силам  , и обобщенной силы  , соответствующей неконсервативным силам  :

= + .  

Если на рассматриваемую систему действуют только консервативные силы, то обобщенная сила определяется формулой:

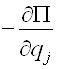=  =  (j=1,2,…, s).

В этом случае уравнения Лагранжа второго рода принимают следующий вид:

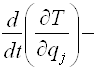
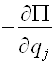=  (j = 1,2,…, s). (11)

Уравнения (12) можно преобразовать путем введения функции Лагранжа L = Т – П, называемой кинетическим потенциалом.

П = П ( t).

Следовательно, кинетический потенциал L является функцией обобщенных координат, обобщенных скоростей и времени:

Потенциальная энергия является функцией только обобщенных координат и времени, а потому

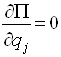 (j=1,2,…, s).

Пользуясь этим условием, получим

, 

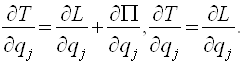
Подставим эти частные производные в уравнения Лагранжа (11):

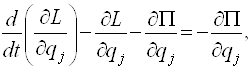
или

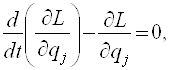 (j=1,2,…, s). (12)

Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной с

27 не весь

Взаимодействие тел, при котором за малый промежуток времени  скорости точек изменяются на конечную величину, называется ударом. Время удара  измеряется сотыми, тысячными и менее долями секунды. Силы, возникающие при таком взаимодействии, называются ударными.

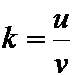  или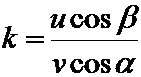 

Основное уравнение теории удара. Изменение количества движения материальной точки за время удара равно сумме ударных импульсов, действующих на точку

,                                   (3.9.2)

где   – скорость материальной точки до удара,   – скорость этой точки после удара,   – импульс ударных сил.

величина, равная импульсу ударной силы F _уд за время удара t, наз. ударнымимпульсом