В начало лекции
19.3. Принцип виртуальных перемещений
Для равновесия механической системы с идеальными и стационарными связями необходимо и достаточно, чтобы сумма виртуальных работ всех активных сил, приложенных к точкам системы, была равна нулю
.
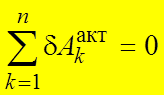Доказательство
необходимости. Дано,
что механическая система находится в
равновесии и требуется доказать,
что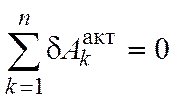 
. Так
как система
находится в равновесии, то равнодействующая
активных сил 
и
равнодействующая сил реакций связей 
,
приложенных в 
-й
точке системы, удовлетворяют условию
равновесия статики:
, 
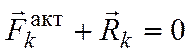Сообщим
системе виртуальное перемещение и
умножим обе части каждого равенства
скалярно на соответствующее виртуальное
перемещение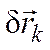 
.
Далее, суммируя полученные равенства,
находим:
.
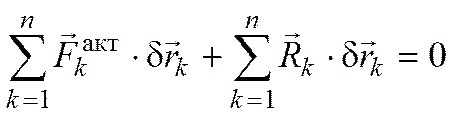Так как связи идеальные, то
.
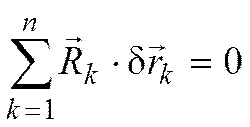
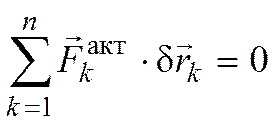
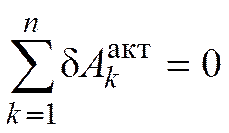Доказательство
достаточности. Пусть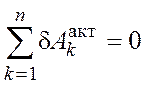 
,
докажем, что механическая система
находится в равновесии. Предположим,
что при заданных условиях система не
находится в равновесии, т. е. при действии
на систему активных сил хотя бы одна
точка получила действительное
перемещение 
и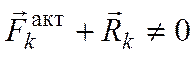 
.
Так
как для стационарных связей действительное
перемещение совпадает с одним из
возможных (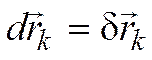
),
то 
или 
по
крайней мере для одной точки системы,
вышедшей из равновесия. Суммируя по
всем точкам системы, получаем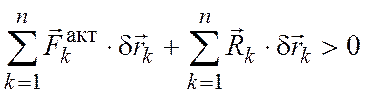 
.
Так
как связи идеальные,
то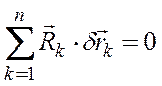 
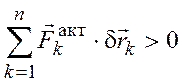
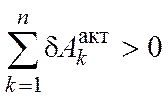, что
противоречит условию.
Следовательно, система находится в равновесии.
Принцип
виртуальных перемещений может быть
записан в иной форме, если поделить
уравнение, выражающее этот принцип на
временной интервал 
,
в течение которого совершается это
перемещение.
Отношение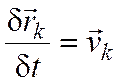 
называется виртуальной
скоростью. Необходимое и достаточное
условие равновесия записывается в
виде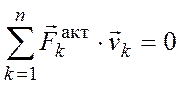 
или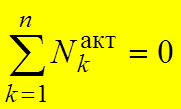 
.
То есть, для равновесия механической системы с идеальными и стационарными связями необходимо и достаточно, чтобы сумма мощностей всех активных сил на виртуальных скоростях точек их приложения была равна нулю.
Принцип виртуальных перемещений можно применять для определения реакций связей в статически определимых конструкциях. Для этого надо освободить систему от одной из связей и реакцию этой связи считать активной силой. Система, лишенная одной связи, может получить виртуальное перемещение, что и позволяет найти неизвестную реакцию.
В начало лекции
Число независимых между собою возможных перемещений системы называетсячислом степеней свободы этой системы. Например. шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет 6 степеней свободы.
Общее
уравнение динамики 
–
при движении системы с идеальными
связями в каждый данный момент времен
сумма элементарных работ всех приложенных
активных сил и всех сил инерции на любом
возможном перемещении системы будет
равна нулю. Уравнение использует принцип
возможных перемещений и принцип Даламбера
и позволяет составить дифференциальные
уравнения движения любой механической
системы. Дает общий метод решения задач
динамики. Последовательность составления:
а) к каждому телу прикладывают действующие
на него задаваемые силы, а также условно
прикладывают силы и моменты пар сил
инерции; б) сообщают системе возможные
перемещения; в) составляют уравнения
принципа возможных перемещений, считая
систему находящейся в равновесии.
23