Ификация связей

Т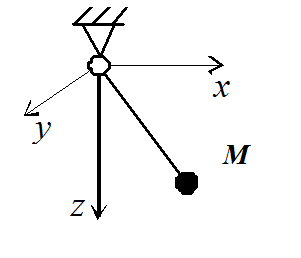 ела, ограничивающие свободу перемещения точек данной механической системы, называются связями.    

 

В аналитической механике связи задаются математически с помощью уравнений или неравенств, в которые входят время, координаты всех или части точек системы и их производные по времени. В частности, для одной точки уравнение связи может иметь вид:   ,  где   – заданная функция координат точки. Например, связь в виде идеального стержня длины   (рис. 19.1), ограничивающего перемещение материальной точки  , записывается уравнением   . 

Д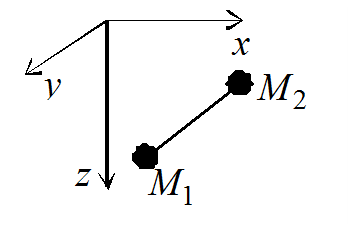 ругой пример (рис. 19.2). При свободном движении системы двух материальных точек   и  , соединенных между собой идеальным стержнем длины  , уравнение связи, из условия неизменности расстояния между точками, имеет вид:   .  Положение данной системы определяется пятью независимыми параметрами, в качестве которых могут быть выбраны три декартовы координаты точки   и две декартовы координаты точки  , или три декартовы координаты точки   и два сферических угла, определяющих положение отрезка  .

 

 

Связь называется голономной, если в уравнение связи входят только координаты точек механической системы или иные параметры, определяющие ее положение в пространстве.  .

 

Выше были рассмотрены примеры голономных связей.  Если уравнения связи, кроме координат и иных параметров, определяющих положение системы, содержат их дифференциалы или производные по времени и эти дифференциальные уравнения не могут быть проинтегрированы, то связь называется неголономной.

Примером неголономной связи служит горизонтальная плоскость для диска радиуса  , катящегося по ней без скольжения и поворачивающегося при этом вокруг вертикального направления (рис. 19.3). В данном случае проекции скорости центра диска на оси координат определяются равенствами  ,  ,    .

Последнее уравнение может быть проинтегрировано и дает  . Первые два преобразуются к виду    ,      .  Эти дифференциальные уравнения могут быть проинтегрированы только в случае, когда   . При этом связь становится голономной. В дальнейшем ограничимся рассмотрением только голономных связей.

 

С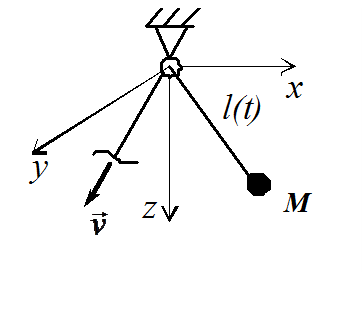 вязь называют удерживающей, если она выражается математически равенством, и неудерживающей, если она выражается неравенством.

Связь называется стационарной, если в уравнение связи время явно не входит. Если в уравнение связи время входит явным образом, то связь −нестационарная. 

 

 

Примером нестационарной связи, наложенной на материальную точку, является нить (рис. 19.4), длина которой изменяется согласно некоторому закону 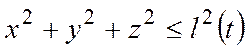   .  Это голономная, неудерживающая, нестационарная связь.

 

В начало лекции

 

 

19.2. Виртуальные перемещения. Виртуальная работа силы.  Идеальные связи

Виртуальным (возможным) перемещением точки (обозначается  ) называется такое бесконечно малое (элементарное) перемещение, которое допускается в рассматриваемый момент движения наложенными на точку связями. 

Проекции вектора виртуального перемещения точки   называются вариациями координат.

 

В случае голономной нестационарной связи уравнение   в фиксированный момент определяет некоторую поверхность в трехмерном пространстве, на которой находится движущаяся точка. Виртуальные перемещения лежат в касательной плоскости к этой поверхности (рис. 19.5) и вариации координат удовлетворяют уравнению      ,

выражающему перпендикулярность вектора нормали к поверхности 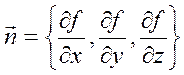  и вектора  . 

 

По форме левая часть этого уравнения совпадает с полным дифференциалом функции трех переменных. Она называется вариацией функции   и обозначается  .

 

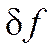То есть   .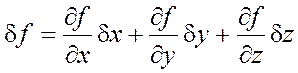 

 

При условии    с точностью до величин второго порядка малости координаты точки   в новом ее положении удовлетворяют уравнению связи   .  Действительно,

,

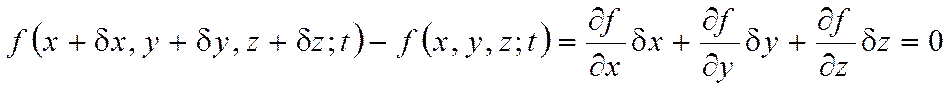откуда   .

 

Если на точку наложена стационарная связь  , то ее уравнение задает поверхность, по которой движется эта точка, и бесконечно малое действительное перемещение   совпадает с одним из виртуальных. Например, для связи в виде стержня (рис. 19.1) и виртуальное перемещение   точки   и ее действительное перемещение   перпендикулярны радиусу сферы, по которой может перемещаться точка.

Если задана неудерживающая связь неравенством  , то при нахождении виртуального перемещения она заменяется  удерживающей  .

 

Виртуальным перемещением механической системы называется совокупность виртуальных перемещений точек этой системы.

 

Например, виртуальным перемещением кривошипно-ползунного механизма (рис. 19.6), являются два элементарных поворота – кривошипа на угол 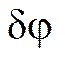  вокруг оси вращения и шатуна на угол   вокруг мгновенного центра скоростей. Из геометрических соображений следует, что:    .  Связь между виртуальными перемещениями отдельных тел и точек, образующих механическую систему, в общем случае может быть найдена аналитически путем варьирования уравнений связи.

 

 

 

 

 

 

 

 

 

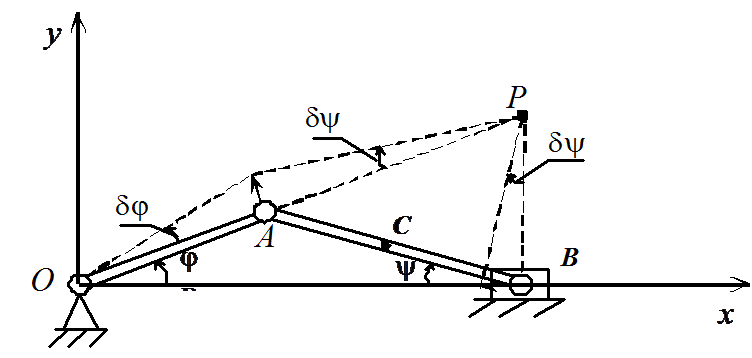
В частности, в предыдущем примере из уравнения голономной и стационарной связи    находим  

Вариации координат середины шатуна  находятся из уравнений связи

 

 

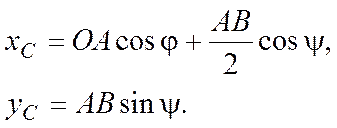
Виртуальной работой силы (обозначается 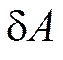 ) называется  работа силы на виртуальном перемещении точки ее приложения, т.е.:   .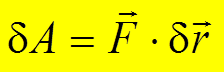

Связь называется идеальной, если сумма работ реакций этой связи  на любом виртуальном перемещении системы равна нулю.   

 

 

 

 

 

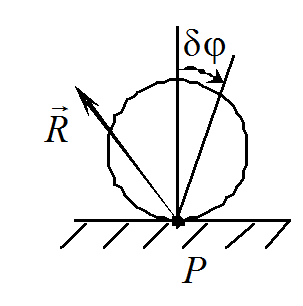
   Примером является шероховатая поверхность для катка (рис. 19.7), катящегося без скольжения, при отсутствии трения качения 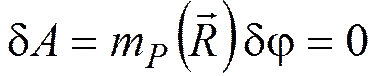   .