Начало документа

17.2. Приведение системы сил инерции твердого тела к простейшему виду

По теореме Пуансо систему сил инерции, приложенных к точкам твердого тела, в общем случае можно заменить силой и парой сил. Сила приложена в центре приведения и равна главному вектору сил инерции, момент пары равен главному моменту сил инерции относительно центра приведения. 

Поскольку  ,  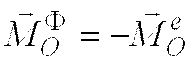, применяя теорему о движении центра масс и теорему об изменении кинетического момента, находим: 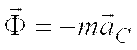  , 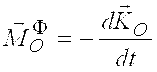      .  Здесь за центр приведения   принята  произвольная неподвижная точка в инерциальной системе отсчета.  Обычно за центр приведения выбирается центр масс механической системы.

Тогда с учетом теоремы об изменении кинетического момента в поступательно движущейся с центром масс системе отсчета   ,     .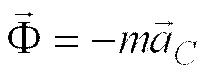

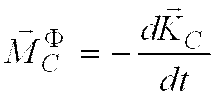Рассмотрим частные случаи движения твердого тела.

1) При поступательном движении твердого тела выбирая за центр приведения центр масс системы, находим, что  главный момент сил инерции относительно центра масс равен нулю

.

То есть система сил инерции приводится к равнодействующей, которая приложена в центре масс и определяется равенством    .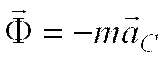

2) При вращении тела, имеющего плоскость материальной симметрии, вокруг оси, проходящей через центр масс  перпендикулярно этой плоскости  выбирая за центр приведения неподвижную точку (рис. 17.3), совпадающую с центром масс, находим, что  . Система сил приводится к паре сил, лежащей в плоскости материальной симметрии тела. Вектор момента этой пары определяется равенством 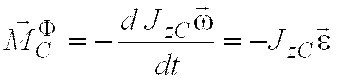  .   Алгебраический момент пары сил инерции может быть вычислен по формулам: 

.

3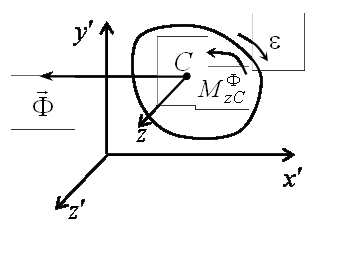 ) При плоском движении твердого тела, имеющего плоскость материальной симметрии в качестве центра приведения выбираем центр масс, расположенный в плоскости симметрии тела, которая перемещается в координатной плоскости  (рис. 17.4). Так как плоское движение может быть представлено как сложение поступательного движения с центром масс и вращательного вокруг оси  , проходящей через центр масс, то система сил инерции приводится к силе и к паре, лежащей в плоскости материальной симметрии   ,   ,  где   − момент инерции  относительно оси, проходящей через центр масс, перпендикулярно плоскости материальной симметрии. 

4) Аналогично рассматривается приведение системы сил инерции при вращении тела, имеющего плоскость материальной симметрии, вокруг оси, не проходящей через центр масс. При этом за центр приведения может выбираться как центр масс, так и неподвижная точка на оси вращения (рис. 17.5). Если в качестве центра приведения принимается точка  , лежащая на оси вращения в плоскости симметрии, то главный момент сил инерции равен    ,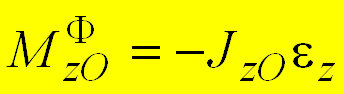

где 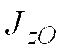  - момент инерции тела относительно оси вращения  .

Начало документа

21

4. Определение реакций в опорах вращающегося тела

Определим реакции в опоре вращающегося тела методом кинетостатики. Он заключается в решении задачи динамики средствами (уравнениями) статики. Для каждой точки механической системы справедливо основное уравнение динамики:

(4.1)

Здесь и – масса и ускорение некоторой точки системы; – сумма всех активных сил и реакций связей, приложенных к ней.

Основному уравнению динамики (4.1) можно придать вид уравнения статики:

(4.2)

Здесь – сила инерции точки механической системы.

Рисунок 4.1. Определение реакций в опорах вращающегося тела

Для заданной механической системы уравнение статики (4.2) имеет вид:

(4.3)

Для определения реакции шарнира нам необходимо и достаточно взять за координатные оси – неподвижные оси и , и определить составляющие реакции шарнира на эти оси:

(4.4)

Отсюда:

Подставив значения сил, получим:

(4.5)

Теперь спроецируем (4.2) на неподвижную ось :

(4.6)

Отсюда:

Подставив известные значения сил, получим:

(4.7)

Полную реакцию в шарнире можно найти по формуле: , где и определяются выражениями (4.5) и (4.7); график её зависимости от времени приведён в приложении к курсовой работе (рис. 4).

24

Уравнения Лагранжа 2-го рода:   , (i=1,2…s) – дифференциальные уравнения второго порядка, s – число степеней свободы системы (число независимых координат); q_i – обобщенная координата (перемещение, угол, площадь и др.);  – обобщенная скорость (линейная скорость, угловая, секторная и др.),

Т = Т(q₁,q₂,…,q_S, , … ,t) – кинетическая энергия системы, Q_i – обобщенная сила (сила, момент и др.), ее размерность зависит от размерности обобщенной координаты и размерности работы.

Для вычисления обобщенной силы, например Q₁, задаем возможное перемещение, при котором все вариации обобщенных координат, кроме q₁, равны нулю:

q₁0, q₂= q₃=…= q_S= 0. Вычисляем на этом перемещении возможную работу А₁ всех активных сил, приложенных к системе. Имея  А₁= Q₁q₁,находим  .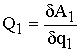

Если силы, действующие на систему, потенциальные (консервативные) (например, силы тяжести, силы упругости), то  ,   П = П(q₁,q₂,…,q_S,t) – потенциальная энергия.

Вводится функция Лагранжа:  L = T – П, тогда 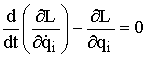   – уравнения Лагранжа второго рода для консервативной системы.

При стационарных связях (связях, не зависящих от времени) t не входит в выражение для кинетической энергии, тогда 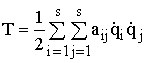  – квадратичная форма обобщенных скоростей,  a_ij= a_ji – коэффициенты инерции. Квадратичная форма всегда положительна.

22

ВЕРНУТЬСЯ   

Основы аналитической механики

Возможные (виртуальные) перемещения системы (s, ) – любая совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент наложенными на систему связями. Возможные перемещения рассматривают как величины первого порядка малости, пренебрегая при этом величинами высших порядков малости. Т.е. криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к их траекториям.

Число независимых между собою возможных перемещений системы называетсячислом степеней свободы этой системы. Например. шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет 6 степеней свободы.

Возможная (виртуальная) работа А – элементарная работа, которую, действующая на матер.точку сила могла бы совершить на возможном перемещении этой точки.

Связи являются идеальными, если сумма элементарных работ реакций этих связей при любом возможном перемещении системы равна нулю, т.е. А^r=0.

Принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении была равна нулю.    или в проекциях:  .

Принцип возможных перемещений дает в общей форме условия равновесия для любой механической системы, дает общий метод решения задач статики.

Если система имеет несколько степеней свободы, то уравнение принципа возможных перемещений составляют для каждого из независимого перемещений в отдельности, т.е. будет столько уравнений, сколько система имеет степеней свободы.