6.3. Теорема об изменении кинетического момента

механической системы

 

            Рассмотрим систему, состоящую из N материальных точек, и запишем для каждой из них соотношение (6.11)

,

где, как уже отмечалось,   – равнодействующие всех внешних и внутренних сил, приложенных к j-й точке системы.

            Сложим почленно полученные уравнения:

.                        (6.12)

Из 2-го свойства внутренних сил следует, что  . Преобразуя левую часть уравнения (6.12)

,

получим из него

,                                (6.13)

где  – главный момент внешних сил системы относительно центра О.

            Итак, доказана следующая теорема. Производная по времени от кинетического момента механической системы относительно неподвижного центра равна главному моменту внешних сил системы относительно того же центра.

            Векторному уравнению (6.13) соответствуют три уравнения в проекциях на оси координат:

,                      (6.14)

где   – главные моменты внешних сил относительно осей x, y, z. Следует отметить, что уравнения вида (6.14) рекомендуется использовать при рассмотрении системы, в состав которой входит тело, вращающееся вокруг неподвижной оси. Тогда, совмещая одну из координатных осей с осью вращения, получим уравнение, не содержащее неизвестных реакций опор вращающегося тела.

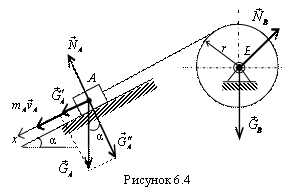             Пример 1. Груз А, спускаясь по гладкой наклонной плоскости, приводит во вращение барабан В посредством намотанного на него троса (рис. 6.4).

            Определить зависимость угловой скорости барабана от времени, если известны масса груза  , момент инерции барабана   относительно его оси вращения z, перпендикулярной плоскости рисунка, радиус барабана r и угол наклона α плоскости к горизонту. Массой троса пренебречь и учесть, что в начальный момент времени система находилась в состоянии покоя.

            На систему, состоящую из груза А и барабана В, действуют внешние силы: сила тяжести груза   и сила тяжести барабана  , нормальная реакция наклонной плоскости   и реакция оси барабана  .  Направим ось z вдоль оси  вращения  барабана  к нам и используем

3-е уравнение системы (6.14):

.                                         (6.15)

Кинетический момент системы относительно оси z равен сумме кинетических моментов груза и барабана. Принимая поступательно движущийся груз за материальную точку, получим

.

Так как  , окончательно запишем

.                                    (6.16)

            Для определения главного момента внешних сил относительно оси z разложим силу   на составляющие   и  , направленные вдоль наклонной плоскости и по нормали к ней. Силы   и   равны по модулю и направлены вдоль одной прямой в противоположные стороны, поэтому сумма их моментов относительно оси z равна нулю. Силы  и   не имеют моментов относительно оси z, так как их линии действия пересекают эту ось. Таким образом,  главный момент внешних сил относительно оси z

.            (6.17)

Теперь подставим (6.16) и (6.17) в уравнение (6.15)

,

откуда получим

.

Проинтегрируем это дифференциальное уравнение, учитывая пределы изменения переменных:

;

.

            Сформулируем следствия из этой теоремы:

            1) внутренние силы не влияют непосредственно на изменение кинетического момента механической системы, а их косвенное влияние осуществляется через внешние силы (см. замечание в подразделе 5.5);

2) если главный момент внешних сил относительно некоторого неподвижного центра на рассматриваемом промежутке времени равен нулю, то кинетический момент системы относительно этого центра остается постоянным. Положив в уравнении (6.13)  , получим, что

   и    ;

            3) если главный момент внешних сил относительно некоторой неподвижной оси на рассматриваемом промежутке времени равен нулю, то кинетический момент системы относительно этой оси остается постоянным. Действительно, если  , то из 1-го уравнения (6.14) получим                              и  .

            Второе и третье следствия выражают закон сохранения кинетического момента механической системы.

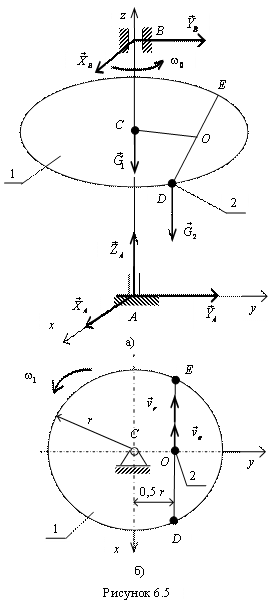
Пример 2. В точке D обода однородного диска 1, вращающегося вокруг неподвижной вертикальной оси с угловой скоростью  , находится точечный груз 2, масса которого в два раза меньше массы диска (рис. 6.5а.). В некоторый момент времени груз, являющийся самоходным механизмом, начинает двигаться по хорде DЕ. Радиус диска равен r, СО = 0,5r.

Определить угловую скорость диска   при прохождении груза через середину хорды О, если в этот момент скорость груза относительно диска равна   (рис. 6.5б). Силами сопротивления пренебречь.

             Рассмотрим систему, состоящую из диска 1 и груза 2. На нее действуют внешние силы: сила тяжести диска  , сила тяжести груза   и составляющие реакций опор    . Моменты всех этих сил относительно оси z равны нулю, поэтому главный момент внешних сил   и кинетический момент системы относительно оси z не изменяется, т.е.  . Следовательно,  , где   – начальный и конечный кинетические моменты системы, соответствующие положениям груза в точках D и O.

            В начальный момент времени диск и груз представляют собой одно тело, вращающееся вокруг оси z, поэтому

;

 

;

.                                          (6.18)

В конечный момент времени кинетический момент системы равен сумме кинетических моментов диска и груза:

,                      (6.19)

где   – абсолютная скорость груза,  . Относительная   и переносная   скорости груза в точке О направлены вдоль хорды DE,

;

Из равенства (6.19) следует, что

.   (6.20)

Приравнивая правые части равенств (6.18) и (6.20)

,

получим  .

15

еорема об изменении кинетического момента системы материальных точек в относительном движении по отношению к центру масс.