Теорема об изменении количества движения

 Количество движения материальной точки – векторная величина, равная произведению массы точки на вектор ее скорости.

 Количество движения механической системы – векторная величина, равная геометрической сумме (главному вектору) количества движения всех точек системы или количество движения системы равняется произведению массы всей системы на скорость ее центра масс.

 Когда тело (или система) движется так, что ее центр масс остается неподвижным, то количество движения тела равно нулю   (например, вращение тела вокруг неподвижной оси, проходящей через центр масс тела). 

 Если движение тела сложное, то количество движения не будет характеризовать вращательную часть движения при вращении вокруг центра масс. Т.е., количество движения   характеризует только поступательное движение системы (вместе с центром масс).

 Импульс силы характеризует действие силы за некоторый промежуток времени.

 Импульс   силы   за конечный промежуток времени   определяется как интегральная сумма соответствующих элементарных импульсов

Теорема об изменении количества движения материальной точки (в дифференциальной форме):

 Производная по времени от количества движения материальной точки равна геометрической сумме действующих на точку сил.

 Теорема об изменении количества движения материальной точки (в интегральной форме):

Изменение количества движения материальной точки за некоторый промежуток времени равняется геометрической сумме импульсов сил, приложенных к точке за этот промежуток времени.

 Теорема об изменении количества движения механической системы (в дифференциальной форме):

 Производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил.

 Теорема об изменении количества движения механической системы (в интегральной форме):

 Изменение количества движения системы за некоторый промежуток времени равняется геометрической сумме импульсов внешних сил, действующих на систему, за тот же промежуток времени.

Закон сохранения количества движения системы.

ИМПУЛЬС СИЛЫ

Перевод

ИМПУЛЬС СИЛЫ

       

мера действия силы за нек-рый промежуток времени; равняется произведению ср. значения силы Fcp на время t1 её действия:

S=Fcpt1.

И. с.— величина векторная, и направлен он так же, как Fср. Точное значение И. с. за промежуток времени t1 определяется интегралом:

При движении матер. точки под действием силы F её кол-во движения получает за время t1 приращение, равное И. с.: S=mv1-mv0 (mv0 и mv1— соотв. кол-во движения точки в начале и в конце промежутка времени t1.

Понятие И. с. широко используется в механике, в частности в теории удара, где величина, равная импульсу ударной силы Fуд за время удара t, наз. ударным импульсом.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ИМПУЛЬС СИЛЫ

- величина, характеризующая действие, к-рое оказывает на тело сила F за нек-рый промежуток времени t₁; равна произведению ср. значения этой силы на время её действия: S=F_cp.t₁. И. с.- величина векторная и направлена так же, как F_cp. Более точно И. с. определяется интеграл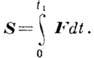ом При движении материальной точки под действием силы её количество движения получает за время t₁ прирашение, равное И. с. Т. о.,mv₁=mv₀+S, где mv₀ и mv₁ - соответственно кол-ва движения точки в начале и в конце промежутка времени t₁.Понятием И. с. широко пользуются в механике, в частности в теории удара, где величина, равная пмпульсу ударной силы F _уд за время удара t, наз. ударнымимпульсом 

Количество движения

Перевод

Количество движения

        мера механического движения, равная для материальной точки произведению её массы m на скорость v. К. л. mv — величина векторная, направленная так же, как скорость точки. Иногда К. д. называют ещё импульсом. При действии силы К. д. точки изменяется в общем случае и численно и по направлению; это изменение определяется вторым (основным) законом динамики (см. Ньютона законы механики).

         К. д. Q механической системы равно геометрической сумме К. д. всех её точек или произведению массы М всей системы на скоростьv_c её центра масс: Q = ∑m_kv_k=Mv_с. Изменение К. д. системы происходит под действием только внешних сил, то есть сил, действующих на систему со стороны тел, в эту систему не входящих. Согласно теореме об изменении К. д. Q₁—Q₀ = ∑S_k^e. где Q₀ и Q₁ — К. д. системы в начале и в конце некоторого промежутка времени, S_k^e — импульсы внешних сил F_k^e (см. Импульс силы) за этот промежуток времени (в дифференциальной форме теорема выражается уравнением  _k^e_{). Этой теоремой пользуются при решении многих задач динамики (См.Динамика), в частности в теории Удара.}

         _{Для замкнутой системы, т. е. системы, не испытывающей внешних воздействий, или в случае, когда геометрическая сумма действующих на систему внешних сил равна нулю, имеет место закон сохранения К. д. При этом К. д. отдельных частей системы (например, под действием внутренних сил) могут изменяться, но так, что величина Q = ∑mкvk остаётся постоянной. Этот закон объясняет такие явления, как реактивное движение, отдачу (или откат) при выстреле, работу гребного винта или вёсел и др. Например, если рассматривать ружье и пулю как одну систему, то давление пороховых газов при выстреле будет для этой системы силой внутренней и не может изменить К. д. системы, равное до выстрела нулю. Поэтому, сообщая пуле К. д. m1v1, направленное к дульному срезу, пороховые газы сообщат одновременно ружью численно такое же, но противоположно направленное К. д. m2v2, что вызовет отдачу; из равенства m1v1 = m2v2 (где v1, v2 — численные значения скоростей) можно, зная скорость v1; пули при вылете из ствола, найти наибольшую скорость v2 отдачи (а для орудия — отката).}

         _{При скоростях, близких к скорости света с, К. д., или импульс, свободной частицы определяется формулой р = mv/ β=v/c; когда v<<c, эта формула переходит в обычную: р = mv (см. Относительности теория).}

         _{К. д. обладают и Поля физические (электромагнитные, гравитационные и др.). К. д. поля характеризуются плотностью К. д. (отношением К. д. элементарного объёма к этому объёму) и выражается через напряжённость поля или его потенциал и т.д.}

         _{О К. д. элементарных частиц см. Квантовая механика.}

   

14